
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Колес для построения статистической функции распределения и гистограммы распределения случайных величин


Оценка вероятности противоположного события — безотказной работы

а вероятность безотказной работы (при N →∞) за время ti

Так как безотказная работа и отказ — взаимно противоположные события, то сумма их вероятностей равна единице:

В начальный момент наблюдений при t1 = 0 Σmt = 0 и F(t) = 0, а Р(t) = 1. Если наблюдения вести достаточно долго (теоретически до tt =∞), то Σmt = N, F(t) = 1, а Р(t)=0.
На основании опытных данных по формуле (8) можно определить статистическую вероятность безотказной работы в каждый момент времени и построить зависимость статистической функции вероятности безотказной работы Р(t) (кривая 3). Эта кривая наглядно показывает изменение вероятности безотказной работы в зависимости от времени в пределах 0 ≤ Р (t) ≤ 1. Следует иметь в виду, что без указания конкретного периода времени t значение Р (t) смысла не имеет. Например, нельзя сказать, что вероятность безотказной работы грузового каната Р(t) = 0,9. Правильным будет указание вероятности безотказной работы лишь вместе с наработкой, к которой она относится, например вероятность работы грузового каната Р(t) = 0,9 за время t = 300 ч. Это означает, что в среднем 90 % установленных канатов определенного качества проработают при определенных условиях 300 ч и более без замены, а 10% канатов придется заменить до истечения 300 ч работы. Чем больше значение Р(t) при данном ti тем выше безотказность объекта. Как видно из рис. 2, а, кривые Р (t) и F (t) симметричны одна другой.
Функции, подобные F(t), в теории вероятностей называют интегральными, а функции, подобные f (t), — дифференциальными. Дифференциальную функцию f(t) можно получить из интегральной F (t) дифференцированием ее:

И, наоборот, интегральную функцию F (t) можно получить интегрированием функции f(t).
Наряду с функциями Р(t), F(t) и f(t) в теории надежности важное значение имеет функция λ(t) интенсивности отказов или функция условной плотности вероятности возникновения отказа невосстанавливаемого объекта. Статистически она определяется в зависимости от плана испытаний.
Планы испытаний на надёжность с измерением наработки
В процессе эксплуатации металлургического оборудования в соответствии с положением о ТО и Р предусмотрено ведение документации об отказах оборудования. Фактически в них регистрируются результаты наблюдений за работой оборудования, т.е. осуществляется испытание на надёжность. Внедрение информационной системы об отказах оборудования, позволяет повысить эффективность и достоверность проводимых испытаний (наблюдений).
В зависимости от принятой системы и методов ремонта применяются различные планы испытаний. Существуют 14 разновидностей планов испытаний с измерением наработок. Каждый план имеет условное обозначение в виде трёх (четырёх) буквенных символов, заключенных в квадратные скобки.
На первой позиции символом N указывается объём выборки.
На второй позиции проставляется один из следующих символов, характеризующих план испытаний:
U - отказавшие изделия не заменяются и не восстанавливаются;
R- отказавшие изделия заменяются новыми;
М - работоспособность изделия восстанавливается после каждого отказа.
На третьей позиции записывается один или два символа, указывающие на окончание испытаний:
N - отказ всех изделий, поставленных на испытания;
r - отказ г изделий (г ≤ N) или наступление г отказов;
Т - по истечении определённого времени (наработки);
z - при наработке zi каждого изделия, где z i=min(t j, τi), i=1…N;
ti- наработка до отказа i-го изделия;
Ti - наработка до снятия с испытаний работоспособного i-ro изделия.
То есть по этому плану испытания прекращаются при достижении наработки z с учётом как наработок изделий до отказа, так и наработок работоспособных изделий, но снятых с испытаний по тем или иным причинам (плановые замены), если величина этой наработки меньше z.
На третьей позиции может записываться и сочетание 2-х символов, например (r ,Т), это означает, что испытания прекращаются либо при появлении r отказов, либо по истечении времени Т, если к этому моменту времени не произошло г отказов.
Поясним на некоторых примерах, как расшифровываются планы испытаний.
Так, при испытаниях по плану [NUN], если выражение в квадратных скобках имеет вид [10U101, то это означает, что исследуется 10 объектов, которые при отказах не заменяются и не восстанавливаются; испытания завершаются отказом всех 10 объектов.
Для плана |NMT| выражение [4 М 150] означает, что испытываются 4 объекта, изделия восстанавливаются после каждого отказа, испытания прекращаются при достижении 150 сут.
При плане |NRr] выражение |10 R 5] характеризует испытание на надёжность 10 объектов, при котором отказавшие изделия заменяются новыми, испытание прекращается, когда произойдут отказы 5 объектов.
План [NUz] в виде выражения [10 Uz] трактуется следующим образом: на испытание поставлено 10 объектов, которые при отказах не восстанавливаются и не заменяются; испытания прекращаются, когда из всех объектов одна часть изделий откажет, а другая часть изделий будет снята с испытаний в произвольный момент времени. В плане [NUTr] выражение [10 U (100,5)] показывает, что 10 испытываемых объектов при отказах не заменяются и не восстанавливаются, испытания прекращаются через 100 сут, если ранее не произошло отказа 5 объектов.
При выборе плана испытаний для металлургических агрегатов и машин необходимо учитывать следующие факторы:
* металлургические агрегаты (машины) являются сложными, непрерывно действующими техническими системами;
* существует график остановки агрегатов на плановые текущие ремонты для восстановления исходных показателей надёжности;
* вследствие высокой интенсификации производства для металлургических машин характерна высокая интенсивность отказов;
* восстановление исходных показателей надёжности, а также работоспособного состояния осуществляется либо путём замены изношенной (отказавшей) детали, либо путём замены уз
ла, в состав которого входит изношенная (отказавшая) деталь.
Поэтому для деталей, узлов и машин металлургических агрегатов наиболее применимы планы типа [R] и [М]. Но результаты испытаний по планам [R] сводимы к результатам по планам [U| путём переноса начала испытаний каждого объекта к некоторому условному началу испытаний всех объектов.
Планы типа [М| можно интерпретировать как планы |U|, если положить, что каждая наработка между отказами соответствует некоторому условному невосстанавливаемому объекту; восстановление работоспособного состояния объекта после отказа полное.
Планы типа [U] или приводимые к нему, кроме плана [NUN], предусматривают снятие объектов с испытаний до наступления отказа. Такое событие называется цензурированием.
Различают три типа цензурирования:
I тип - при заданной наработке;
IIтип - при заданном числе отказов;
III тип - случайное.
Первый тип цензурирования соответствует плану [NUT], второй тип цензурирования - плану [NUr], третий тип - плану [NUz].
Наработка объекта от начала испытания до наступления цензурирования (прекращения испытаний) называется наработкой до цензурирования.
Выборка, элементами которой служат значения наработки до отказа и наработки до цензурирования, называется цензурирован-ной выборкой.
Различают однократно и многократно цензурированные выборки.
Однократно цензурированная выборка - цензурированная выборка, в которой значения всех наработок до цензурирования равны между собой.
Многократно цензурированная выборка - цензурированная выборка, в которой значения всех наработок до цензурирования не равны между собой.
Однократно цензурированная выборка характерна для планов [NUT] и [NUr]. Для плана в общем случае характерна случайно цензурированная выборка, т.е. выборка может быть как однократно, так и многократно цензурированной. В зависимости от принятой системы технического обслуживания для металлургических машин возможны следующие планы испытаний с учётом приведения к плану типа [U]:
[NUN] - замена детали или узла производится только после отказа;
[NUT| - замена детали или узла производится после отказа или в каждый плановый ремонт, если в межремонтный период отказа не произошло;
[NUz] - замена детали или узла производится после отказа или в плановый период, наработка до которого есть величина случайная.
Существует 14 разновидностей планов испытаний. Наиболее употребительными являются планы испытаний [N, U, Т] и [N, U, r]. Согласно первому плану испытывают N объектов; отказавшие во время испытаний объекты не восстанавливают и не заменяют, испытания прекращают при истечении времени Т испытаний или наработки для каждого неотказавшего объекта. Второй план испытаний отличается от первого тем, что испытания прекращают, когда число отказавших объектов достигнет r; при r = N имеем план [N, U, N).B обозначениях планов испытаний под U подразумевают невосстанавливаемые объекты.
При плане испытаний [N, U, Т] интенсивность λ(t) отказов статистически определяется отношением


Рис. 3. Зависимость λ(f) для сорбитизированных ходовых колес мостовых кранов
где r(t+Δt) — число отказов за время t +Δt; r (t) — число отказов за время t; N (t) — количество объектов, работоспособных ко времени t; N(t+ Δt) — количество объектов, работоспособных ко времени t + Δt; Δt — продолжительность интервала времени.
Так как N(t) N (t + Δt) =Δr — число отказов за время Δt, а N (t) =N r (N — общее число испытуемых объектов, r — число отказов за время t), то выражение (12) можно представить в более удобном виде:

При разных значениях Δt для объектов исследуемой совокупности знаменатель в выражении (13) целесообразно представлять в виде ΣΔti; тогда

По данным табл. 1 построена зависимость статистической функции интенсивности отказов λ(t) крановых колес (рис. 3). При увеличении количества опытных данных и времени испытаний, т. е. при N →∞и t →∞, статистическая функция распределения интенсивности отказов приближается к теоретической функции λ(t).
Можно показать, что между λ(t) и другими рассмотренными функциями f(t), F(t) и Р(t) существует тесная связь. Поделив числитель и знаменатель в выражении (13) на NΔt, на основании выражений (4) и (8) с учетом того, что тi = Δr, lt = Δt, Σmt =r, получим

При увеличении числа испытуемых объектов и времени испытаний, т. е. при N →∞ и t→∞, опытное значение λ’(t) стремится к λ(t) и зависимость (14) принимает вид

Используя выражение (11), связь по формуле (15) можно представить в следующем виде:

После интегрирования выражения (16) имеем
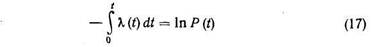
или

Наряду с функциями F(t), f(t) и Р(t) по выражениям (10), (11), (16), (18) важной характеристикой надежности объекта является среднее время Т его безотказной работы, определяемое в теории вероятностей как

Подставив значение f(t) из выражения (11) в выражение (19) и проинтегрировав его по частям, получим

Так как Р(0) = 1, а Р(∞) = 0 и Р(f) →0 быстрее, чем t →∞, то tP (t)  = 0, и выражение (20) примет вид
= 0, и выражение (20) примет вид

ЗАКОНЫ НАДЕЖНОСТИ
Закон распределения случайной величины, закон надежности — аналитическое соотношение, устанавливающее связь между значениями случайной величины (наработки, времени восстановления и др.) и их вероятностями. Оценка функций надежности статистическими методами требует проведения испытаний, больших по объему и длительных по срокам, что не всегда осуществимо. Поэтому получаемая статистическая информация о надежности характеризует ее лишь в пределах данного объема и времени испытаний. Ее ценность существенно возрастает, если известен вид функции надежности для данного объекта или подобного ему, которая в наибольшей мере согласуется с опытным распределением случайной величины. В теории надежности наибольшее распространение получили следующие законы распределения: для дискретных случайных величин — биноминальный и Пуассона; для непрерывных случайных величин — экспоненциальный, нормальный, Вейбулла, а также гамма-, χ2- и

логарифмически нормальное распределения. Распределения времени восстановления и долговечности кранов и их элементов, как правило, описываются законами экспоненциальным, нормальным и Вейбулла.
Экспоненциальный (показательный) закон распределения случайной величины (рис. 4) в общем виде записывается так:

где Р(t) — вероятность того, что случайная величина имеет значение, большее t; е — основание натуральных логарифмов; к — параметр распределения.
Значения функции у = е-x табулированы.
Для экспоненциального распределения функции вероятности отказа F(t), плотности вероятности отказа f(t) и интенсивности отказов λ(t) имеют вид

Среднее время до возникновения отказа по формуле (21)

Зависимости (22)—(26) показаны на рис. 4, а. Экспоненциальное распределение — однопараметрическое. Оно определяется одним параметром λ,. Из выражений (22) и (26) следует, что вероятность безотказной работы, соответствующая среднему времени Т до возникновения отказа (наработки до отказа),

Экспоненциальный закон соответствует стационарному потоку случайных событий, так как плотность вероятности возникновения отказа λ(t) согласно выражению (25) постоянна и составляет, λ(t)= λ.

При экспоненциальном законе распределения требуется сравнительно небольшая продолжительность испытаний. Так как обычно λ ≤0,1, то формулу (22) в результате разложения в ряд и отбрасывания малых членов можно привести к виду

а поскольку из выражения (26)

то

 Из выражений (27)-(30) следует, что при требуемой вероятности безотказной работы Р(t) = 0,9 период испытаний можно принять 0,1T, а при вероятности 0,99 -всего лишь 0,01T. На основании опытных данных для определения параметра X
Из выражений (27)-(30) следует, что при требуемой вероятности безотказной работы Р(t) = 0,9 период испытаний можно принять 0,1T, а при вероятности 0,99 -всего лишь 0,01T. На основании опытных данных для определения параметра X
достаточно получить оценку средней наработки до отказа Т по формуле (1) или воспользоваться графическим способом (рис. 4, б). Для этого нужно нанести экспериментальные точки в координатах t и lgP(t). Знак «минус» здесь потому, что Р(t) < 1 и, следовательно, lgР (t) отрицательная величина. Логарифмируя выражение (22), получим

Из формулы (31) следует, что тангенс угла наклона прямой, аппроксимирующей экспериментальные точки, tgα = 0,4343, откуда λ =2,3tgα.
Нормальный законраспределения случайной величины t характеризуется тем, что плотность вероятности отказов λ(t) (рис. 5, а) плавно нарастает, достигает максимума и затем плавно падает.
Для этого закона распределения плотность вероятности отказа вероятность отказа и вероятность безотказной работы определяются по формулам:
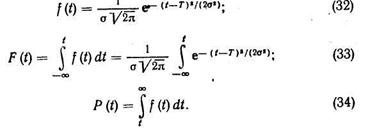
Нормальное распределение — двухпараметрическое. Оно имеет два независимых параметра: математическое ожидание или среднюю наработку на отказ Т, определяемую статистически по формуле (1), и среднее квадратическое отклонение σ, определяемое из выражения (6). Математическое ожидание определяет на кривой Р(t) (рис. 5, б) положение петли, а среднее квадратическое отклонение σ ее ширину. Кривая плотности вероятности f(t) тем острее и выше, чем меньше σ. Теоретически она начинается от f = –∞ и распространяется до t = + оо. Но фактически площадь, очерченная крыльями кривой плотности вероятности отказа f(t) за пределами Т–3σ, настолько мала, что соответствующая ей вероятность отказа составляет всего 0,00135 (0,135%), и обычно ее не учитывают в расчетах. Вероятность до Т–2σ отказа также мала (0,021175 или 2,175%).
На практике вместо расчетов по формулам (32)—(34) используют данные таблиц, например табл. 2, в которой через U обозначено

Распределение Вейбулла. При этом законе распределения случайных величин функция вероятности безотказной работы имеет вид'

 где
где  — параметры закона распределения.
— параметры закона распределения.
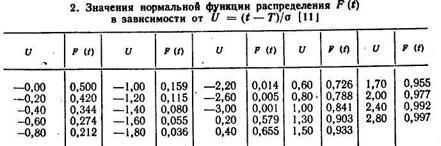

Значения а и b определяют по табл. 3 в зависимости от оценки коэффициента вариации V, вычисляемого по формуле (7).
Для этого закона функция вероятности отказов F (t) имеет вид

ПОКАЗАТЕЛИ НАДЕЖНОСТИ И ИХ ОПРЕДЕЛЕНИЕ
Для решения практических задач по оценке надежности необходимы ее количественные измерители, которые называют показателями надежности. Различают единичные и комплексные показатели. Единичный показатель количественно характеризует только одно свойство надежности объекта, а комплексный может одновременно характеризовать несколько его свойств.
Показатели безотказности. Вероятность безотказной работы — вероятность того, что в пределах заданной наработки или заданного интервала времени t отказ объекта не возникнет. На основании опытных данных статистическая вероятность безотказной работы определяется по формуле (8). Обозначив Σmt через r, где r — число (объектов, отказавших ко времени t, из общего числа наблюдаемых объектов N, работоспособных в начальный момент времени t = 0, получим

где (N — r) — число объектов, проработавших безотказно до момента времени t.
Если отказ связан с дорогостоящей или аварийно опасной задержкой производства, а также для ответственных элементов ПТМ (крюки, валы, зубчатые колеса и др.), рекомендуется принимать Р(t) ≥0,99, а если отказ может привести к несчастному случаю, Р(t) ≥0,9999. Если отказ не связан с тяжелыми последствиями и вызывает незначительные экономические потери, что соответствует практике использования многих ПТМ, то допустимое значение Р (t) в интервале t принимают намного ниже указанного или вообще-этот показатель не нормируют.
Средняя наработка Тг до отказа — математическое ожидание наработки до первого отказа. Ее определяют для невосстанавли-ваемых объектов, таких, как канаты, подшипники качения, крюки и др. При плане испытаний [N, U, N] по ГОСТ 16504—81 этот показатель определяется статистически отношением суммы наработки Σti испытуемых объектов до отказа к количеству наблюдаемых объектов N:

В ряде случаев более наглядны другие показатели безотказности, в частности интенсивность отказов λ(t) и параметр потока отказов ωв. Согласно отраслевому стандарту ПТМ (ОСТ 24.190.03—83) показатель ωв используют в качестве обязательного для ПТМ, внезапный отказ которых может привести к аварии или большим экономическим потерям, а также для машин, перевозящих людей в местах их скопления (лифты административных зданий, эскалаторы и др.). Значение ωв определяют по формуле

где пв — количество внезапных отказов, зарегистрированных в период наблюдения; Σti — наработка за тот же период.
Наработка То на отказ – отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки. Наработку на отказ статистически определяют отношением суммарной наработки Σti восстанавливаемых объектов к суммарному числу No отказов этих объектов:

При экспоненциальном распределении оценка наработки на отказ

При λ = ωв

Наработка на отказ зависит от длительности периода, в течение которого она определяется. Это обусловлено непостоянством характеристик потока отказов. Например, в период приработки наработка на отказ меньше, чем после его окончания. И в период, предшествующий капитальному ремонту или профилактике, она снова уменьшается.
Показатели долговечности. Гамма-процентный ресурс — наработка, в течение которой объект не достигнет предельного состояния с заданной вероятностью γ(%.). Например, если γ = 90%, то соответствующий ресурс называют «девяносто процентным ресурсом».
Для массовых и крупносерийных изделий ПТМ ОСТ 24.190.03—83 устанавливают 90%-ный ресурс до капитального ремонта. Для его определения рекомендуется: установить наблюдение за определенным количеством объектов — N = 10i (где i — целое число не менее 5); зарегистрировать наименьшие ресурсы в количестве i; принять в качестве 90%-ного ресурса наибольший из этих ресурсов. Например, установив наблюдение за 60 кранами, зарегистрировали ресурсы 6 канатов (i = 6) 97, 11О, 121, 130, 138 и 142 дня; 90%-ный ресурс канатов в этих условиях можно принять равным 142 дням. Для определения 80%-ного ресурса пришлось бы продолжить наблюдение до замены еще 6 канатов на любых из 60 наблюдаемых кранах.
В общем виде гамма-процентный ресурс определяют по графику функции Р (t). Например, согласно рис. 2, а (кривая 3) 90%-ный ресурс крановых колес равен приблизительно одному году [вероятность безотказной работы Р(t) — 0,9], 50%-ный (медианный) ресурс — 2,3 года [вероятность безотказной работы Р(t) = 0,5].
Средний ресурс — математическое ожидание ресурса. При наличии данных о ресурсе (сроке службы, сроке сохраняемости) N объектов статистическая оценка среднего ресурса

где xt — ресурсы объектов.
Для невосстанавливаемых изделий особо ответственного назначения используют показатель долговечности, названный назначенным ресурсом. Под ним понимают суммарную наработку объекта, при достижении которой эксплуатация должна быть прекращена независимо от его состояния. Этот показатель используют при установлении периодичности технического обслуживания и ремонта машин.
По ОСТ 24.190.03—83 для ПТМ нормируется средний ресурс до капитального ремонта или до списания, вычисляемый по формуле (43), при этом количество N зарегистрированных величин ресурсов ti рекомендуется принимать не менее 10 (N ≥ 10).
У большинства ПТМ ресурсы до списания велики и нормирование среднего ресурса до списания для них практически не имеет значения из-за отдаленности сроков предъявления претензий о несоблюдении этого показателя.
Показатели ремонтопригодности: вероятность восстановления в заданное время и среднее время восстановления. Первый из них — вероятность того, что время восстановления объекта после отказа не превысит заданного, второй — математическое ожидание времени восстановления. Под временем восстановления подразумевают суммарное время, затрачиваемое на обнаружение, поиск причины и устранение последствий отказа. При наличии статистических данных о длительности τ1, τ2, .... τm восстановления т объектов оценка среднего времени восстановления

Эти показатели ремонтопригодности отраслевыми документами для ПТМ не предусмотрены, хотя в ряде случаев их нормирование целесообразно, например, при использовании ПТМ без резервирования в комплексе с другим технологическим оборудованием, когда длительный простой лишь одной из машин может надолго вывести из строя весь технологический комплекс и повлечь за собой крупные экономические потери.
Показатели ремонтопригодности важны и для таких ПТМ, как лифты, эскалаторы, канатные дороги, фуникулеры и др., длительные простои которых при внезапных отказах хотя и не всегда вызывают прямые экономические потери, но связаны с дезорганизацией движения и большими неудобствами для пользующихся ими.
Показатели сохраняемости: гамма-процентный и средний сроки сохраняемости. Первый показатель — срок сохраняемости, который будет достигнут объектом с заданной вероятностью γ(%), второй — математическое ожидание срока сохраняемости. Сроком сохраняемости называют календарную продолжительность хранения и (или) транспортирования объекта в заданных условиях, в течение и после которой сохраняются значения заданных показателей в установленных пределах. Для многих ПТМ период между отправкой их с завода-изготовителя до подачи в монтаж может исчисляться годами. При соблюдении правил транспортирования и хранения элементы ПТМ, как правило, не изменяют заданных показателей. Но имеются и такие машины, у которых при длительном хранении они существенно ухудшаются. Для них целесообразно нормирование показателей сохраняемости. Методы их определения аналогичны методам определения гамма-процентного и среднего ресурсов.
Комплексные показатели надежности. Известно более 10 таких показателей. Из них три регламентированы отраслевым стандартом ПТМ —ОСТ 24.190.03—83.
Коэффициент готовности определяется отношением суммарного времени пребывания наблюдаемых объектов в работоспособном состоянии  произведению числа N этих объектов на продолжительность Тр эксплуатации за исключением простоев на проведение плановых ремонтов и технических обслуживании:
произведению числа N этих объектов на продолжительность Тр эксплуатации за исключением простоев на проведение плановых ремонтов и технических обслуживании:

где ξi— суммарное время пребывания i-го объекта в работоспособном состоянии (i = 1, 2, 3, ..., N). Поскольку время Тр у различных объектов наблюдаемой группы может не совпадать, значение Кгцелесообразнее определять по выражению

где 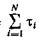 — суммарное время на восстановление работоспособности наблюдаемых объектов после отказа.
— суммарное время на восстановление работоспособности наблюдаемых объектов после отказа.
При порядке обслуживания, предусматривающем немедленное начало восстановления отказавшего объекта, коэффициент готовности

где То — наработка на отказ; Тв — среднее время восстановления.
Как видно из формулы (47), коэффициент готовности объединяет два единичных показателя надежности: наработку на отказ То, характеризующую безотказность, и среднее время Тв восстановления, характеризующее эксплуатационную технологичность.
По РТМ 24.090.23—76 для ПТМ коэффициент Кг готовности принят в качестве допустимого показателя вместо обязательного, называемого коэффициентом простоев Kп, который связан с коэффициентом готовности зависимостью

Из этой зависимости следует, что

Удельная суммарная стоимость ремонтов Су.р. определяется как отношение средней суммарной стоимости ремонтов к математическому ожиданию суммарной наработки объекта за один и тот же период эксплуатации. Под средней суммарной стоимостью ремонтов понимают математическое ожидание суммарных затрат на все виды ремонтов за определенный период эксплуатации. Методика определения Kп и Су.р. для ПТМ приведена в ОСТ 24.190.03—83.
Экспериментальное определение надежности ПТМ и их элементов
Надежность ПТМ и их элементов может определяться экспериментальным путем, для чего проводятся различные испытания. Машины целиком испытываются на стендах, полигонах или в эксплуатационных условиях. Отдельные системы, узлы и детали проходят испытания на специальных стендах. Подъемно-транспортные машины, предназначенные для работы в тяжелых режимах эксплуатации, должны проходить ускоренные испытания на надежность. Испытания этого типа проводятся на заводских полигонах. Цель испытаний – в возможно короткий срок определить износостойкость, циклическую прочность и теплостойкость элементов ПТМ.
Статистические данные по ряду машин длительного использования показали, что большинство характерных отказов происходит при наработке первых 2000 – 4000 ч. Сократить срок выявления слабых узлов возможно при работе с перегрузками. В каждом случае степень допустимой перегрузки при ускоренных испытаниях на надежность должна быть определена соответствующими расчетами устойчивости, прочности и выносливости как машины в целом, так и ее наиболее ответственных элементов. Перегрузки достигают увеличением массы поднимаемого груза, ускорений механизмов при пуске и торможении и рядом других мероприятий.
Ускоренные испытания на надежность делятся на два этапа. На первом этапе проводятся тензометрические измерения нагрузок и напряжений в ответственных элементах при предварительно назначенных перегрузках. Измеряются токи, давления и пр. В результате расчетов прочности, выносливости и изнашивания, выполненных с использованием тензометрических данных, уточняется степень допустимой перегрузки, а для машин циклического действия – характеристики цикла работы.
На втором этапе проводятся длительные испытания с уточненной нагрузкой и последовательностью включений механизмов. Использование машины по времени при испытаниях должно быть максимальным. Расчеты по портальным кранам показали, что время испытаний с перегрузками можно сократить до 1000 машино-часов. Это объясняется тем, что между напряжениями (нагрузками) в деталях и их циклической долговечностью существует степенная зависимость. В связи с этим малые перегрузки могут вызвать значительное уменьшение долговечности ответственных элементов. При испытаниях этого типа желательна установка аппаратуры, частично или полностью автоматизирующая работу и учет наработки машины, а также ее отдельных механизмов. Особенно тщательно должны соблюдаться правила техники безопасности.
Надежность опытных образцов ПТМ определяется при эксплуатационных испытаниях. Продолжительность испытания 2000 – 4000 ч работы. В процессе испытаний выявляется большинство недостатков, связанных с возможными ошибками проектирования и изготовления. В этот период машина должна работать в наиболее тяжелом режиме эксплуатации под особым наблюдением инженерно-технического персонала. На основе статистических данных по потокам отказов и восстановлений производится оценка показателей надежности, которые обычно имеют заниженные значения, так как машины находятся в периоде приработки. Дальнейшие испытания опытных образцов в течение одного-трех лет эксплуатации позволяют определить показатели надежности в период установившейся эксплуатации.
За машинами установочной серии, работающими в наиболее тяжелых режимах, также организуется специальное наблюдение. Собираются и обрабатываются статистические данные по отказам и восстановлениям (ремонтам). В результате определяются показатели надежности этих ГПМ, выявляются узлы и детали, лимитирующие надежность машины в целом, разрабатываются мероприятия по повышению надежности. Испытания проводятся в течение одного–трех лет. Если в результате испытаний необходимо определить закономерности изменения показателей надежности, то проводятся испытания в течение более длительного срока. В процессе испытаний фиксируется наработка в тоннах и (или) в часах машинного времени, регистрируются отказы, проводится их описание, устанавливаются причины отказов и время ремонта. Одновременно должны вестись наблюдения не менее чем за 2-8 машинами. С увеличением количества наблюдаемых машин растет точность определяемых характеристик.
В общем случае планирование испытаний на надежность включает отбор машин, определение объема выборки, продолжительность испытаний. В соответствии с требованиями математической статистики отбираемые для испытаний машины или их узлы и детали должны принадлежать к исследуемой совокупности. Для опытных образцов и образцов установочной серии эти требования сводятся к качественному соответствию машин, так как вообще этих объектов весьма мало. Это означает, что не следует в одну совокупность сводить машины, отличающиеся конструкцией узлов и работающие в различных условиях эксплуатации.
Определительные испытания на надежность могут проводиться по нескольким планам (ГОСТ 1751—79). Планы отличаются условиями, при которых прекращаются наблюдения. Так, план [Nи, И, Nи] означает, что наблюдения ведутся до отказа всех Nи наблюдаемых объектов. План [Nи, R, Т] означает, что наблюдения над Nи объектами ведутся в течение заданного времени Т при условии, что отказавшие образцы заменяются новыми или ремонтируются. План наблюдений выбирается в зависимости от вида объекта, условий эксплуатации и экономической целесообразности.
Объем выборки, т.е. количество испытываемых объектов, зависит от принятого плана наблюдений, требуемой достоверности и точности оценок и предполагаемых значений показателей надежности (ГОСТ 17510-79). Достоверность оценки определяется доверительной вероятностью, которая равна вероятности попадания оценки в принятый интервал. Дело в том, что экспериментальная оценка показателя надежности в связи с ограниченностью любого эксперимента всегда случайна. Однако она должна с принятой доверительной вероятностью лежать в определенном доверительном интервале, который расположен вокруг теоретического значения показателя надежности. Точность оценки характеризуется относительной шириной этого интервала. При незавершенных или так называемых усеченных испытаниях, когда не все наблюдаемые объекты отказали, объем выборки определяется приближением.
Важным вопросом является определение влияния различных эксплуатационных условий работы на показатели надежности. Испытания на надежность всегда длительны и требуют значительных средств. Поэтому важно при определении количества испытаний использовать теорию планирования эксперимента, которая позволяет получить максимум информации при минимуме экспериментов. Для того чтобы показать возможности этой теории, рассмотрим следующий пример. Предположим, что требуется определить влияние таких факторов, как технологический вариант работы (Х1), квалификация управления (Х3) и уровень технического обслуживания (Х2), на коэффициент готовности (Kr) грейферных портальных кранов. Для определения значимости этих факторов надо собирать статистические данные по потокам отказов и восстановлению работающих кранов. Каждый фактор будем варьировать на двух уровнях. Это значит, что испытания проводятся при двух технологических вариантах работы кранов (например, варианты судно – вагон и склад – склад), при двух квалификациях крановщиков (I и III разряды), при двух уровнях технического обслуживания (высокий и низкий). Необходимое количество опытов при полном факторном эксперименте определяется по формуле
 ,
,
где  - число уровней факторов;
- число уровней факторов;  - количество факторов. В нашем случае
- количество факторов. В нашем случае  = 2,
= 2,  = 3 и количество опытов
= 3 и количество опытов  . При этом реализуются все возможные сочетания уровней факторов.
. При этом реализуются все возможные сочетания уровней факторов.
В табл. 2 приведена соответствующая матрица эксперимента. Каждый опыт в данном случае состоит в наблюдении в течение года за двумя–восьмью кранами, работающими в определенных эксплуатационных условиях. Например, опыт 1 состоит в том, что ведется наблюдение за двумя–восьмью кранами, работающими по варианту судно – вагон. Эти краны управляются крановщиками III разряда. Уровень технического обслуживания машин высокий, что означает регулярное смазывание всех точек, предусмотренных заводской инструкцией, правильную и своевременную регулировку пусковой и тормозной аппаратуры и т.д. Опыт 2 заключается в том, что ведется наблюдение за двумя–восемью кранами, которые работают по тому же технологическому варианту и управляются крановщиками I разряда. Уровень технического обслуживания - низкий (нерегулярное смазывание, регулировка, нарушается график планово-предупредительных ремонтов и т.д.). Проведя все эти наблюдения, можно установить, пользуясь определенными правилами, какие из трех рассмотренных факторов значимы и, следовательно, какие из них надо учитывать при оценке коэффициента готовности. Если учесть, что каждый кран испытывается в течение года, а всего под наблюдением находится от 8 × 2 = 16 до 8 × 8 = 64 кранов, то становятся очевидным сложность и высокая стоимость этих испытаний. Применяя теорию планирования эксперимента, можно значительно сократить количество опытов. Для этого используются так называемые дробные факторные планы, позволяющие уменьшить число опытов в несколько раз и в то же время выявить главные закономерности, связывающие коэффициент готовности с тремя факторами. Так, если по предварительным соображениям можно пренебречь совместным влиянием факторов Х1 (технологический вариант работы крана) и Х2 (уровень технического обслуживания), то можно построить сокращенную в два раза матрицу эксперимента, которая обозначается 23-1 (табл. 3). В ней всего четыре опыта.
После предварительной оценки и анализа собранной информации по показателям надежности ПТМ осуществляется статистическая обработка экспериментальных данных. Обработка включает в себя оценку однородности статистических данных, определение параметров распределения исследуемых случайных величин (например, ресурс детали), проверку согласия экспериментального распределения с теоретическим и расчет показателей надежности. Анализ однородности статистических данных проводится для определения возможности объединения материалов, полученных из различных мест эксплуатации, в одну выборку. Проверка однородности выполняется по различным критериям (Смирнова, Стьюдента, Фишера и др.).
Таблица 2
Матрица полного факторного плана 23
| Номер опыта | Уровни фактора | Среднее значение коэффициента готовности | ||
| Х1 | Х2 | Х3 | ||
| -1 -1 +1 +1 -1 -1 +1 +1 | -1 +1 -1 +1 -1 +1 -1 +1 | +1 -1 -1 +1 -1 +1 +1 -1 | Kr1 Kr2 Kr3 Kr4 Kr5 Kr6 Kr7 Kr8 |
Примечание: +1 – верхний уровень фактора; -1 – нижний уровень фактора.
Таблица 3
Матрица дробного факторного плана 23-1
| Номер опыта | Уровни фактора | Среднее значение коэффициента готовности | ||
| Х1 | Х2 | Х3 | ||
| +1 -1 +1 -1 | +1 -1 -1 +1 | +1 +1 -1 -1 | Kr1 Kr2 Kr3 Kr4 |
Примечание: +1 – верхний уровень фактора; -1 – нижний уровень фактора.
Оценка параметров (математического ожидания, среднего квадратичного отклонения и т.п.) распределения может быть точечной и интервальной. Точечная оценка дает приближенную оценку параметра, которая должна быть состоятельной, несмещенной, эффективной. В ГОСТ 27.503-81 приведены зависимости для оценки параметров различных законов распределения случайных величин (например, ресурса детали) при различных планах эксперимента; в ГОСТ 11.008–75 – правила построения вероятностных сеток (системы координат), с помощью которых возможна удобная для практических целей графическая оценка параметров. Интервальные оценки параметров позволяют оценить доверительные пределы, в которых лежит точечная оценка с определенной доверительной вероятностью.
Проверка первоначально принятой гипотезы о виде закона распределения случайной величины может осуществляться в первом приближении графически по виду гистограммы или по расположению точек эмпирической функции распределения на вероятностной сетке. Оценка показателей надежности ПТМ и их элементов осуществляется по точечным оценкам параметров законов распределения. В ГОСТ 27.501-81 для ряда законов распределения ресурса, времени восстановления и т.д. приведены зависимости, с помощью которых осуществляется точечная оценка показателей надежности. Известны методы определения доверительных интервалов, в которых с определенной вероятностью лежат теоретические показатели надежности.
При проведении испытаний на надежность важно выяснить, какие узлы и детали в наибольшей степени влияют на показатели надежности. Для этого используют относительные коэффициенты восстановлений (kвi) и отказов
(kот i) , определяемые по следующим зависимостям:
 ;
;  ,
,
где tвi, nот i - время восстановления и количество отказов по узлу (детали); tв, nотi – общее время восстановления и общее количество отказов за рассматриваемое время. Узлы и детали с наибольшими kвi и kотi - лимитируют надежность ПТМ в целом и при выполнении работ по ее повышению требуют первоочередной модернизации.
Надежность узлов и деталей ПТМ можно определить по статистическим данным, полученным в процессе эксплуатации. В табл. 4 приведены обобщенные данные по различным источникам относительно типов законов распределения ресурса некоторых деталей ПТМ.
Различие в законах распределения по одним и тем же элементам объясняется особенностями условий эксплуатации и конструкции самих элементов. Так, нормальный закон распределения ресурса грузовых канатов объясняется тем, что эти элементы ПТМ достаточно однородны в силу стабильности технологии изготовления и подвергаются изнашиванию с постоянной интенсивностью. В то же время на кранах, при определенных технологических вариантах работы, отказы канатов связаны с их перетиранием о комингсы люков грузовых судов, соскакиванием с канатных блоков и с рядом других случайных причин. В этом случае ресурс распределяется по экспоненциальному закону.
Таблица 4
Дата добавления: 2015-01-29; просмотров: 300; Мы поможем в написании вашей работы!; Нарушение авторских прав |