
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ЗАДАНИЯ К РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЕ № 2
Рисунок 1.16 Рисунок 1.17 Рисунок 1.18
Рисунок 1.19 Рисунок 1.20 Рисунок 1.21

Рисунок 1.22 Рисунок 1.23 Рисунок 1.24
Рисунок 1.25 Рисунок 1.26 Рисунок 1.27
Рисунок 1.28 Рисунок 1.29 Рисунок 1.30
Таблица 1.1.
| Номер группы | Е1, В | Е2, В | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом |
Задача1.2.Для нелинейной электрической цепи, схема которой изображена на рисунках 1.31 - 1.36:
1. Построить входную вольтамперную характеристику цепи;
2. Определить токи во всех ветвях цепи и напряжения на отдельных элементах, используя вольтамперные характеристики и данные таблицы 1.3.
Рисунок 1.31 Рисунок 1.32 Рисунок 1.33
Рисунок 1.34 Рисунок 1.35 Рисунок 1.36
Указания к выбору варианта: в зависимости от порядкового номера группы по таблице 1.3 выбрать напряжение на входе цепи и сопротивления линейных элементов, а по таблице 1.2 - характеристики нелинейных элементов в соответствии с порядковым номером студента в журнале группы. Вольтамперные характеристики приведены на рисунке 1.37.
 |
Рисунок 1.37
Таблица 1.2
| Порядковый номер студента в журнале группы | Номер схемы | Тип характеристики | Порядковый номер студента в журнале группы | Номер схемы | Тип характеристики | ||
| НЭ1 | НЭ2 | НЭ1 | НЭ2 | ||||
| 1.31 | а | - | 1.34 | б | - | ||
| 1.32 | а | б | 1.35 | б | а | ||
| 1.33 | а | б | 1.36 | б | а | ||
| 1.32 | а | в | 1.35 | б | в | ||
| 1.33 | а | в | 1.36 | б | в | ||
| 1.34 | а | - | 1.31 | в | - | ||
| 1.35 | а | б | 1.32 | в | а | ||
| 1.36 | а | б | 1.33 | в | а | ||
| 1.35 | а | в | 1.32 | в | б | ||
| 1.36 | а | в | 1.33 | в | б | ||
| 1.31 | б | - | 1.34 | в | - | ||
| 1.32 | б | а | 1.35 | в | а | ||
| 1.33 | б | а | 1.36 | в | а | ||
| 1.32 | б | в | 1.35 | в | б | ||
| 1.33 | б | в | 1.36 | в | б |
Таблица 1.3
| Номер группы | ||||||||||
| U,B | ||||||||||
| R3,Ом | ||||||||||
| R4,Ом |
Типовой расчет к задаче 1.1.
Пример1.Методом эквивалентных преобразований определить токи в ветвях цепи, схема которой приведена на рисунке 1.38 , если Е= 120В, R1= 14 Ом, R2=20 Ом, R3=10 Ом, R4=20 Ом, R5=25 Ом, R6=16 Ом. Расчет проверить составлением баланса мощности.
Р е ш е н и е.
Рисунок 1.38 
| R23 =  = =  =4 Ом ;
R34 = =4 Ом ;
R34 =  = =  = 4 Ом;
R42 = = 4 Ом;
R42 =  = =  = 8 Ом; = 8 Ом;
|
Укажем направление токов в ветвях. Заменим треугольник сопротивлений abc эквивалентной звездой
Получаем новую схему (рисунок 1.39), эквивалентное сопротивление которой легко найти путем параллельного и последовательного сложения сопротивлений
 = 30 Ом.
= 30 Ом.
Ток в неразветвленной части цепи I1 =  =4 А.
=4 А.
Для определения токов I5 и I6 найдем напряжение U fd
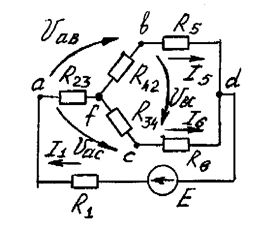 Рисунок 1.39
Рисунок 1.39
| Ufd = Rfd I1= E - (R1+R23) I1= 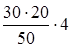 = 48 B,
отсюда I5 = = 48 B,
отсюда I5 =  = 1,6 A,
I6 = = 1,6 A,
I6 =  = 2,4 A.
Расчет тока I2 выполним по закону Ома для участка цепи ab(рисунок 1.38)
I2 = = 2,4 A.
Расчет тока I2 выполним по закону Ома для участка цепи ab(рисунок 1.38)
I2 =  =1,44 A, =1,44 A,
|
где по второму закону Кирхгофа для контура abfa в схеме рисунка 1.39
Uab = R23 I1 + R42I5= 4×4 +8×1,6 = 28,8 B.
Аналогично
I3 =  =2,56 A
=2,56 A
или I3 = I1 - I2 = 4 - 1,44 =2,56 A,
I4 =  = –0,16 A
= –0,16 A
или I4 = I2 - I5 = 1,44 - 1,6 = – 0,16 A.
Минус означает, что положительное направление тока I4 будет противоположно указанному на схеме.
Правильность расчета проверим составлением баланса мощности:
EI1 = R1I12+ R2I22+ R3I32+ R4I42+ R5I52+ R6I62; 480 = 480 (ВТ)
Пример2.Используя метод двух узлов, найти токи в ветвях цепи рисунка 1.40, если E1=20 B, E2=40 B, E3=10 B, E4=50 B, R1=15 Ом, R2=10 Ом, R3=9 Ом, R4=11 Ом, R5=5 Ом.
Построить потенциальную диаграмму для любого замкнутого контура.
Решение.Направим токи в ветвях к узлу аи определим напряжение между узлами
Uab=  = 35 B
= 35 B
| Рисунок 1.40 | Токи в ветвях рассчитаем по закону Ома:
I=  =(±E±Uab) q;
I1 = =(±E±Uab) q;
I1 =  A;
I2 = A;
I2 =  А;
I3 = А;
I3 =  = =  =0,25 А. =0,25 А.
|
Положительное направление тока в первой ветви от узла а. Так как направление ЭДС Е1 противоположно направлению тока I1, то источник ЭДС Е1 работает в режиме потребителя.
Потенциальную диаграмму построим для контура acdfbma. Выберем обход контура по часовой стрелке. Обозначим точки, потенциалы которых будем определять, и произвольно примем потенциал одной любой точки равным нулю, например, jа=0. Тогда потенциал точки свыше jа на величину ЭДС Е3
jс = jа+Е3 =10В;
jd = jc + R3I3 = 10+9× 0,25 = 12,25 В;
jf = jd - E4 =12,25-50= -37,75 B;
jb =jf+R4I3 =-35 B; jm= jb+E2=5 B; jа= jm-R2I2= 5 -10× 0,5=0,
что говорит о правильности проведенного расчета.
 |
Для построения потенциальной диаграммы выбираем масштабы для сопротивления mR и потенциаловmj. По оси абсцисс откладываем сопротивления в том порядке, в каком производится обход контура. По оси ординат откладываем потенциалы точек (рисунок 1.41).
Рисунок 1.41
Пример3.Для цепи по схеме рисунка 1.40 определить ток во второй ветви методом эквивалентного генератора.
Решение.
По методу эквивалентного генератора I2 =  =
= 
 .
.
Для определения ЭДС эквивалентного генератора размыкаем ветвь с сопротивлением R2 и находим напряжение холостого хода Uamx=Eэ (рисунок 1.42)
Ix =  =
= 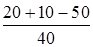 = -0,5 А,
= -0,5 А,
 Рисунок 1.42
Рисунок 1.42
 Рисунок 1.43
Рисунок 1.43
| Uamx= E1 -E2 -(R1+R5)Ix = =20-40-(15+5)(-0,5)= = -10 В
Для определения входного сопротивления исключаем источники ЭДС в схеме рис. 1.42. и сворачиваем пассивную часть цепи относительно зажимов а и m (рис. 1.43).
Rаmbx=  = = = =  = =10 Ом
Ток в ветви I2= = =10 Ом
Ток в ветви I2=  = =  = -0,5 А. = -0,5 А.
|
Знак минус означает, что направление тока I2 противоположно направлению Uam.
Типовой расчет к задаче1.2.
Пример 1. Известны параметры цепи (рисунок 1.44,а): R1=50 Ом, R2=100 Ом. Вольтамперная характеристика нелинейного элемента I3(Uab) дана на рисунке 1.45. Напряжение на зажимах цепи U=200В.
Построить входную вольтамперную характеристику цепи I1(U), определить токи в ветвях и напряжения на участках цепи

а) б)
Рисунок 1.44
Решение. Используем графический метод расчета, при котором сохраняется такой же порядок, как и при расчете линейных цепей, но из-за наличия нелинейных элементов замену эквивалентными сопротивлениями отдельных участков, а затем и всей цепи производим сложением соответствующих ВАХ.
Строим ВАХ для резистора R2. Это будет прямая, выходящая из начала координат, поэтому для ее построения достаточно определить координаты еще одной точки. Произвольно задаемся напряжением, допустим U =100 В, и по закону Ома определяем ток резистора
I =  =
=  = 1 А.
= 1 А.
Используя координаты U = 0, I = 0; U = 100 В, I = 1 А получаем ВАХ I2(Uab) резистора R2 . Аналогично строим ВАХ I1(U1) для резистора R1.
Для получения входной ВАХ I1(U) заменяем нелинейный элемент НЭ1 и резистор R2 , соединенные параллельно, одним эквивалентным нелинейным элементом НЭ (рисунок 1.44,б). Вольтамперная характеристика эквивалентного нелинейного элемента I1(Uab) строится графическим суммированием по оси токов вольтамперных характеристик I3(Uab) и I2(Uab).
 |
Рисунок 1.45
Схема упростилась и представляет теперь последовательное соединение резистора R1 и нелинейного элемента НЭ (рисунок 1.44,б). Суммируя по оси напряжения их вольтамперные характеристики I1(U1) и I1(Uab), получаем результирующую вольтамперную характеристику I1(U), которая и является входной ВАХ цепи.
По заданному напряжению U=200 В на входной ВАХ находим ток I1=2,9 А (точка А). Используя схему рисунка 1.44,б, определяем напряжения на участках. По току I1 на ВАХ I1(U1) резистора R1 находим напряжение U1 =145 В (точка В). По току I1 на ВАХ нелинейного элемента I1(Uab) находим напряжение Uab =55 В (точка С).
Зная напряжение Uab на параллельных элементах НЭ1 и R2 (рисунок 1.44,а) и используя ВАХ I3(Uab) и I2(Uab), определяем токи I3 =2,35 А (точка Д) и I2 =0,55 А (точка Е). 
ЗАДАНИЯ К РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЕ № 2
Анализ электрического состояния однофазных
и трехфазных цепей синусоидального тока
Задача2.1. К зажимам электрической цепи подключен источник синусоидального напряжения u=Umsin(wt+Yu), В частотой f =50 Гц. Амплитуда, начальная фаза напряжения и параметры элементов цепи заданы в таблице 2.1. Схемы замещения цепи приведены на рисунках 2.1 - 2.30.
Задание: 1. Начертить схему замещения электрической цепи, соответствующую варианту, рассчитать сопротивления реактивных элементов цепи.
2. Определить действующие значения токов во всех ветвях цепи.
3. Записать уравнение мгновенного значения тока источника.
4. Определить показание ваттметра и составить баланс активных и реактивных мощностей.
5. Рассчитать напряжения на каждом элементе цепи.
6. Построить векторную диаграмму токов, совмещенную с топографической векторной диаграммой напряжений.
Указания к выбору варианта: порядковый номер студента в журнале группы определяет номер схемы (рисунки 2.1- 2.30), а порядковый номер группы - выбор числовых данных в таблице 2.1.
 Рисунок 2.1 Рисунок 2.2 Рисунок 2.3
Рисунок 2.1 Рисунок 2.2 Рисунок 2.3
 Рисунок 2.4 Рисунок 2.5 Рисунок 2.6
Рисунок 2.4 Рисунок 2.5 Рисунок 2.6
 Рисунок 2.7 Рисунок 2.8 Рисунок 2.9
Рисунок 2.7 Рисунок 2.8 Рисунок 2.9
 Рисунок 2.10 Рисунок 2.11 Рисунок 2.12
Рисунок 2.10 Рисунок 2.11 Рисунок 2.12
Рисунок 2.13 Рисунок 2.14 Рисунок 2.15
 Рисунок 2.16 Рисунок 2.17 Рисунок 2.18
Рисунок 2.16 Рисунок 2.17 Рисунок 2.18

Рисунок 2.19 Рисунок 2.20 Рисунок 2.21
 Рисунок 2.22 Рисунок 2.23 Рисунок 2.24
Рисунок 2.22 Рисунок 2.23 Рисунок 2.24

Рисунок 2.25 Рисунок 2.26 Рисунок 2.27
 Рисунок 2.28 Рисунок 2.29 Рисунок 2.30
Рисунок 2.28 Рисунок 2.29 Рисунок 2.30
Таблица2.1
| Номер | Um, | Yu , | R1 | R2 | R3 | L1 | L2 | C1 | C2 | |
| группы | В | град. | Ом | мГн | мкФ | |||||
| 79,5 | 127,2 | 127,2 | 79,5 | |||||||
| 63,6 | 127,2 | 79,5 | ||||||||
| -45 | 254,4 | 63,5 | 39,8 | |||||||
| 127,2 | 190,8 | 39,8 | ||||||||
| 127,2 | 63,6 | |||||||||
| 238,5 | 42,5 | 19,9 | ||||||||
| 508,8 | 31,8 | 19,9 | ||||||||
| -20 | 127,2 | 79,5 | ||||||||
| 190,8 | 95,4 | |||||||||
| 63,6 | 31,8 |
Задача 2.2. В четырехпроводную трехфазную сеть включены три однофазных приемника и один симметричный трехфазный приемник. Номинальные напряжения сети и приемников даны в таблице 2.2, номинальные мощности и род нагрузки в таблице 2.3.
Задание:1. Рассчитать сопротивления элементов схемы замещения приемников, используя их номинальные данные в таблицах 2.2. и 2.3.
2. На основании таблицы 2.2 выбрать и начертить схему включения приемников к трехфазной сети.
3. Определить фазные и линейные токи каждого приемника, токи в проводах сети.
4. Построить векторную топографическую диаграмму напряжений, совмещенную с векторной диаграммой токов.
5. Выбрать и начертить схему включения ваттметров для измерения активной мощности всех приемников. Определить показания ваттметров и составить баланс активной мощности.
Указания к выбору варианта: порядковый номер группы определяет номинальные напряжения сети и приемников (таблица 2.2), порядковый номер студента в журнале группы - номинальные мощности и род нагрузки (таблица 2.3.).
Таблица 2.2
| Номер | Линейное напряжение | Номинальное напряжение приемников Uном,В | |
| группы | сети Uл, В | однофазных | трехфазного |
Таблица 2.3
| № с | Однофазные приемники | Трехфазный симмет- ричный приемник | ||||||||||||||
| т | № 1 | № 2 | № 3 | №4 | ||||||||||||
| у д е н т а | Pном, кВт | Qном, квар | cosj | Pод нагр | Pном , кВт | Qном , квар | cosj | Pод нагр | Pном, кВт | Qном , квар | cosj | Pод нагр | Pном кВт | Qном , квар | cosj | Pод нагр |
| 0,8 | инд | 0,6 | емк | емк | ||||||||||||
| 0.9 | емк | 0,6 | инд | |||||||||||||
| инд | емк | 0,7 | инд | 0,5 | емк | |||||||||||
| 0,8 | инд | инд | 0,6 | емк | ||||||||||||
| емк | инд | 0,8 | инд | |||||||||||||
| 0,8 | инд | 0,7 | емк | |||||||||||||
| емк | емк | инд | емк | |||||||||||||
| 0,5 | инд | емк | 0,5 | инд | ||||||||||||
| инд | инд | |||||||||||||||
| 0,7 | емк | 0,5 | инд | 0,8 | инд | |||||||||||
| емк | инд | |||||||||||||||
| 0,6 | инд | 0,8 | емк | инд | 0,7 | емк | ||||||||||
| емк | емк | инд | ||||||||||||||
| 0,8 | инд | 0,8 | инд | 0,8 | инд | 0,9 | емк | |||||||||
| инд | емк | 0,2 | емк | |||||||||||||
| 0,5 | инд | инд | 0,9 | емк | ||||||||||||
| емк | инд | инд | ||||||||||||||
| 0,7 | емк | 0,8 | инд | |||||||||||||
| емк | инд | 0,5 | инд | |||||||||||||
| инд | ||||||||||||||||
| емк | инд | инд | ||||||||||||||
| 0,7 | инд | 0,7 | инд | емк | емк | |||||||||||
| 0,5 | емк | инд | ||||||||||||||
| 0,5 | инд | емк | инд | |||||||||||||
| 0,7 | инд | 0,7 | инд | |||||||||||||
| емк | емк | инд | емк | |||||||||||||
| инд | ||||||||||||||||
| 0,7 | инд | инд | 0,7 | инд | емк | |||||||||||
| 0,5 | емк | инд | 0,6 | инд | ||||||||||||
| емк | емк | 0,8 | инд |
Типовой расчет к задаче 2.1.
К зажимам электрической цепи, схема замещения которой приведена на рисунке 2.31, подключен источник синусоидального напряжения u = 311 sin(wt + 45°) , B частотой f = 50 Гц.
Nbsp; Рисунок 2.31
Параметры элементов схемы замещения: R1 = 5 Ом; R2 = 8 Ом; L1 = 39,8 мГн; L2 = 19 мГн; C1 = 162,5 мкФ; C2 = 192 мкФ.
Задание.
1. Рассчитать реактивные сопротивления элементов цепи.
2. Определить действующие значения токов во всех ветвях цепи.
3. Записать уравнение мгновенного значения тока источника.
4. Определить показание ваттметра и составить баланс активных и реактивных мощностей.
5. Рассчитать напряжения на каждом элементе цепи.
6. Построить векторную диаграмму токов, совмещенную с топографической векторной диаграммой напряжений.
Решение.
1. Реактивные сопротивления элементов цепи
Х1=  =19,6 Ом,
=19,6 Ом,
где w = 2pf = 2× 3,14×50 = 314 1/c;
Х2 = w L1 = 314× 39,8 × 10-3 = 12,5 Ом;
Х3 = w L2 =314× 19 × 10-3 = 6 Ом;
Х4 =  = 16,6 Ом.
= 16,6 Ом.
2. Расчет токов в ветвях цепи выполняем методом эквивалентных преобразований. Находим комплексные сопротивления ветвей, затем участков цепи:
 = R1 - jX1 = 5 - j19,6 =
= R1 - jX1 = 5 - j19,6 =  Ом;
Ом;
 = jX2 = j 12,5 = 12,5 e j90° Ом;
= jX2 = j 12,5 = 12,5 e j90° Ом; 
 = R2 + jX3 = 8 + j6 = 10 e j37° Ом;
= R2 + jX3 = 8 + j6 = 10 e j37° Ом;
 = - jx4 = -j 16,6 = 16,6 e -j90° Ом;
= - jx4 = -j 16,6 = 16,6 e -j90° Ом;
 =
= = 12,5 Ом;
= 12,5 Ом;
 =
=  +
+  = j12,5 +12,5 = 17,7 e j45° Ом.
= j12,5 +12,5 = 17,7 e j45° Ом.
Эквивалентное сопротивление всей цепи можно не определять, так как в данном случае токи первой I1 и второй I2 ветвей можно найти по закону Ома для участка цепи db:
 =
= 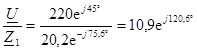 A;
A;
.  =
=  А.
А.
Тогда ток на общем участке цепи (ток источника)
 =
=  +
+  = 10,9 cos 120,6 ° + j10,9sin120,6° + 12,4 = 11,6e j54° A.
= 10,9 cos 120,6 ° + j10,9sin120,6° + 12,4 = 11,6e j54° A.
Для определения токов параллельных ветвей I3 и I4 рассчитаем напряжение на зажимах этих ветвей
 =
=  ×
×  = 12,5 × 12,4 = 155 B;
= 12,5 × 12,4 = 155 B;

 =
=  A;
A;
 =
=  A.
A.
3. Уравнение мгновенного значения тока источника
i = 11,6 ×  sin (wt + 54°) = 16,3 sin (314 t +54°) A.
sin (wt + 54°) = 16,3 sin (314 t +54°) A.
4. Комплексная мощность цепи
 =
=  ·
·  = 220 e j45°× 11,6 e -j54° = 2550 e-j 9° = 2510 - j 400 B×A.
= 220 e j45°× 11,6 e -j54° = 2550 e-j 9° = 2510 - j 400 B×A.
Ваттметр показывает отдаваемую источником активную мощность, которая равна действительной части комплексной мощности
Pw = Pист= Re  =2510 Вт.
=2510 Вт.
Реактивная мощность источника равна мнимой части комплексной мощности
Qист= Im  = - 400 вар
= - 400 вар
(знак минус определяет емкостный характер мощности).
Активная Рпр и реактивная Qпр мощности приемников
Рпр = R1I12 + R2I32 = 5×10,92 +8×15,52 = 2510 Вт;
Qпр = -X1I12 + X2I22 + X3I32 -X4I42 = - 400 вар.
Баланс мощностей выполняется Pист = Pпр; Qист = Qпр.
5. Напряжения на элементах схемы замещения цепи:
Ude = R1I1 = 5×10,9 = 54,5 B;
Ueb = X1I1 = 19,6×10,9 = 214 B;
Uda = X2I2 = 12,5×12,4 = 155 B;
Uac = X3I3 = 6×15,5= 93 B;
Ucb = R2I3 = 8×15,5= 124 B.
6. На комплексной плоскости в масштабе откладываем векторы токов в соответствии с расчетными значениями, при этом положительные фазовые углы отсчитываем от оси +1 против часовой стрелки, а отрицательные – по часовой стрелке. Так , вектор тока  = 10,9 e j120,6°A повернут относительно оси +1 на угол 120,6 ° и длина его в масштабе определяет ток 10,9 А; вектор тока I2=12,4 А совпадает с осью действительных величин и т.д. (рисунок 2.32).
= 10,9 e j120,6°A повернут относительно оси +1 на угол 120,6 ° и длина его в масштабе определяет ток 10,9 А; вектор тока I2=12,4 А совпадает с осью действительных величин и т.д. (рисунок 2.32).

Рисунок 2.32
На топографической векторной диаграмме напряжений каждой точке диаграммы соответствует определенная точка электрической цепи. Построение векторов напряжения ведем, соблюдая порядок расположения элементов цепи и ориентируя векторы напряжения относительно векторов тока: на активном сопротивлении ток и напряжение совпадают по фазе, на индуктивном элементе напряжение опережает ток на угол p/2 , а на емкостном – напряжение отстает от тока на угол p/2. Направление обхода участков цепи выбираем, как принято, противоположно положительному направлению токов. Обход начинаем от точки b, потенциал которой принимаем за исходный (jb=0). Точку b помещаем в начало координат комплексной плоскости. При переходе от точки b к точке е потенциал повышается на величину падения напряжения в емкостном сопротивлении X1. Вектор этого напряжения Ueb отстает по фазе от вектора I1 на угол p/2 . Конец вектора Ueb определяет потенциал точки е . Потенциал точки dвыше потенциала точки ена величину падения напряжения Ude = R1I1 .Вектор Ude откладываем от точки е параллельно току I1 . Конец вектора U de определяет потенциал точки d. Соединив отрезком прямой точки b и d, получим вектор напряжения на зажимах цепи U = Ude = 220 ej45° B.
Аналогично строим векторы напряжений других участков цепи, сохраняя обход навстречу току. От точки b проводим вектор Ucb параллельно вектору тока I3 . Конец вектора Ucb определяет потенциал точки с. От точки с откладываем вектор Uас , опережающий ток I3 на угол p/2 , т.к. участок содержит индуктивное сопротивление X3 . Затем от точки аоткладываем вектор Uda , опережающий I 2 на p /2 . Так как обмотка тока ваттметра имеет пренебрежимо малое сопротивление, то падение напряжения на ней ничтожно и потенциалы точек fи d практически одинаковы. На топографической диаграмме напряжений эти точки совпадают.
Типовой расчет к задаче 2.2.
В четырехпроводную трехфазную сеть линейным напряжением 380 В
включены три однофазных приемника и один симметричный трехфазный приемник, номинальные данные которых приведены в таблице 2.4.
Таблица 2.4
| Номинальные данные | Uном, В | Рном, кВт | Qном, квар | cos j | Род нагрузки | |
| Однофазные | №1 | 4.84 | ||||
| приемники | №2 | 4,84 | индукт. | |||
| №3 | 4,84 | емкост. | ||||
| Трехфазный приемник | №4 | 34,6 | индукт. |
Задание.
1. Рассчитать сопротивления элементов схемы замещения приемников.
2. Выбрать и начертить схему включения приемников к трехфазной сети.
3. Определить фазные и линейные токи приемников, токи в проводах сети.
4. Построить векторную топографическую диаграмму напряжений, совмещенную с векторной диаграммой токов.
5. Выбрать и начертить схему включения ваттметров для измерения активной мощности на зажимах цепи. Определить показания ваттметров и составить баланс активной мощности.
Решение.
1. Сопротивления элементов схемы замещения приемников рассчитываем, используя их номинальные данные в таблице 2.4.
Полное сопротивление однофазного приемника
Z=  cos j или Z=
cos j или Z=  sin j .
sin j .
Активное R и реактивное Х сопротивления
R = Zcos j =  cos2 j ; Х= Zsin j =
cos2 j ; Х= Zsin j =  sin2 j .
sin2 j .
Комплексное сопротивление Z= Ze jj .
Таким образом, для однофазных приемников:
№1 Z1 =  = 10 Ом
= 10 Ом
(реактивная мощность Qном = 0, значит, приемник активный,
cos j =  = 1 ; j = 0),
= 1 ; j = 0),
R1 = 10×1 = 10 Ом, Х1=0, Z1 = 10 e j0 °= 10 Ом;
№2 Z2 =  = 10 Ом
= 10 Ом
(здесь Pном = 0, значит , cos j = 0, sinj = 1, j = +90°, так как род нагрузки индуктивный),
R2 = 0, Х2 = 10 Ом, Z2 = 10 e j90°Ом;
№3 Z3=  ×1 = 10 Ом
×1 = 10 Ом
(cos j = 0 и Рном = 0, а sinj = – 90°, так как род нагрузки емкостный),
Z3 = 10 e -j90° Ом.
Полное сопротивление симметричного трехфазного приемника
№4 Z4 =  cos j ,
cos j ,
где Pном = 3UномIном cos j
или Z4=  sin j =
sin j =  × 0,6 = 10 Ом,
× 0,6 = 10 Ом,
sinj =  = 0,6;
= 0,6;
R4 = Z4 cos j = 10 ×0,8 = 8 Ом, Х4 = Z4 sin j = 6 Ом,
Z4 = 8+ j6 =10 e j37° Ом.
2. Схема включения приемников определяется в зависимости от их номинального напряжения Uном и линейного напряжения трехфазной сети Uл. Если Uном=Uл, то используется соединение треугольником. Если же Uном=Uф=Uл/  , то звездой.
, то звездой.
Таким образом, однофазные приемники с Uном = 220 В необходимо подключить к трехфазной сети с Uл = 380 В по схеме звезды. Так как приемники несимметричны Z1 ¹ Z2 ¹ Z3 , то необходим нейтральный провод, который обеспечит равенство по величине фазных напряжений приемников Uном=Uф=Uл/  =220 В. Схема включения приемников к трехфазной сети приведена на рисунке 2.33.
=220 В. Схема включения приемников к трехфазной сети приведена на рисунке 2.33.
 |
Рисунок 2.33
3. Определяем фазные и линейные токи приемников. С этой целью запишем комплексные действующие значения фазных напряжений сети, совместив вектор UА с осью действительных величин (рисунок 2.34).
U А = U а = 220 е j 0° = 220 В;
U В = U в =220 е -j120° В;
U С = Uс =220 e +j120°B.
Тогда линейные напряжения сети (они же фазные напряжения приемника, соединенного треугольником)
U АВ = U ав = 380 ej30° B;
U BC = U bc = 380 e -j90°B;
U CA = U ca = 380 e j150° B.
Фазные (они же линейные) токи однофазных приемников
I 1=  = 22 A;
= 22 A;
I 2=  = 22 e -j210° = -19 + j11A;
= 22 e -j210° = -19 + j11A;
I 3=  = 22 e j210° = -19 - j11A.
= 22 e j210° = -19 - j11A.
Ток нейтрального провода
 |
IN = I1 + I2+ I3 = 22 - 19 + j 11 - 19 - j 11 = -16 A
Рисунок 2.34
Фазные токи симметричного трехфазного приемника
Iab=  = 38e-j7°= 37,7 - j4,64 A;
= 38e-j7°= 37,7 - j4,64 A;
Ibc=  = 38e- j127°= -22,8 - j30,36 A
= 38e- j127°= -22,8 - j30,36 A
или Ibc= Iab e-j120° = 38 e j (-7°-120°) = 38 e-j127° A ;
Ica=  = 38e j113°= -14,9 +j35A
= 38e j113°= -14,9 +j35A
или Ica= Iab e j120°= 38 e j(-7°+120°) = 38 e j113° A.
Линейные токи симметричного трехфазного приемника
Iа = Iab - Ica = 52,6 - j39,64=66e-j37° A;
Ib = Ibc -Iab = -60,5- j25,72 = =66e - j157° A;
Ic = Ica - Ibc = 7,9+ j65,36 = 66 e j83° A.
Токи в линейных проводах сети определяем по первому закону Кирхгофа:
IА = I1 + Iа = 22+ 52,6- j39,64= 74,6 - j39,64= 84,5е -j28° A;
IВ = I2 + Ib = -79,5 -j14,72= 81е j190,5° A;
IC = I3 + Ic = -11,1 + j54,36 = 55,3е j101,5°A.
4. Для построения векторной топографической диаграммы напряжений векторы фазных Ua, Ub, Uc, затем линейных Uab, Ubc, Uca напряжений размещаем на комплексной плоскости (рисунок 2.35). Вершины a, b, c треугольника напряжений определяют потенциалы соответствующих точек цепи.
 |
Векторы токов однофазных приемников I1, I2, I3 откладываем от начала координат комплексной плоскости в соответствии с расчетными значениями. Вектор I1 совпадает по фазе с вектором Ua , так как приемник №1 чисто активный, вектор I2 отстает по фазе от Ub на p/2 , поскольку приемник №2 индуктивный и вектор I3 опережает по фазе Uc на p/2 , так как приемник №3 емкостный. Вектор тока IN строим согласно уравнению IN = I1+ I2+I3. Векторы фазных токов Iab, Ibc, Ica симметричного трехфазного приемника, имеющего Z4 = 10ej37° Ом, ориентируем относительно напряжений Uab, Ubc,Uca . Токи отстают по фазе от напряжений на 37°.
Рисунок 2.35.
Линейные токи симметричного приемника №4 определяем разностью векторов фазных токов Ia= Iab - Ica; Ib= Ibc- Iab; Ic= Ica - Ibc.
Для построения вектора тока IА = I1+ Iа с конца вектора I1 откладываем вектор Iа и получаем результирующий вектор IА . Аналогично строим векторы
IВ = I2+ Ib ; IС = I3+ Iс .
5. Измерение активной мощности в трехфазных цепях может осуществляться методом одного, двух или трех ваттметров. Метод одного ваттметра используется лишь в симметричных цепях, метод двух ваттметров пригоден для трехпроводных цепей при любой асимметрии. В четырехпроводных цепях применяется метод трех ваттметров. Анализируемая цепь четырехпроводна, и мы должны использовать метод трех ваттметров. Схема их включения дана на рисунке 2. 33.
Показание каждого ваттметра определяется напряжением, приложенным к его обмотке напряжения, током, протекающим по обмотке тока, и косинусом угла сдвига фаз между напряжением и током:
PA= UAIAcos(YUA-YIA) = 220 ×84,5cos(0° +28°) = 16,38 кВт;
PB= UBIBcos(YUB-YIB) = 220 ×81cos(-120° -190,5°) = 11,53 кВт;
PC= UCICcos(YUC-YIC) = 220 ×55,3cos(120° -101,5°) = 11,53 кВт.
Активная мощность на зажимах цепи
Pист = PA + P
Дата добавления: 2015-01-29; просмотров: 235; Мы поможем в написании вашей работы!; Нарушение авторских прав |