Краткие сведения о реологических свойствах вязких и застывающих нефтей.

ВВЕДЕНИЕ

Добыча высоковязких нефтей, содержащих большое коли­чество парафина, т.е. застывающих при сравнительно высоких темпеpaтуpax , скаждым годом возрастает. Весьма значительной является выработка высоковязких и высокозастывающих нефтепродуктов. Пере­качка таких жидкостей обычным способом нерациональна, а иногда и невозможна вследствие большого гидравлического сопротивления. Имеется немало способов, позволяющих перекачивать высоковязкие жидкости; во всех случаях каким-то образом повышается текучесть нефти, т.е. снижается гидравлическое сопротивление трубопровода. Самый простой способ - смешение высоковязких и маловязких нефтей и совместная их перекачка. По сути близкими к смешению являются различные виды гидротранспорта, когда в качестве маловязкой жид­кости используется вода. Применение различных присадок-депрессаторов также позволяет снизить гидравлическое сопротивление трубопровода. Текучесть нефти может быть повышена термообработкой ее. Наиболее технологически отработан и получил широкое практическое применение способ предварительного подогрева высоковязкой нефти. В каждом конкретном случае выбор способа перекачки обосновывается технико-экономическими расчетами,

I. ПЕРЕКАЧКА ВЯЗКИХ И ЗАСТЫВАЮЩИХ НЕФТЕЙ

Краткие сведения о реологических свойствах вязких и застывающих нефтей.

Свойства жидкости, от которых зависит характер её течения, называются реологическими.

Поведение жидкостей при движении описывается кривыми течения (рис.1). Для ньютоновских жидкостей присуща линейная зависимость (кривая I) напряжения сдвига от скорости сдвига dw/dr (от градиента скорости течения по радиусу трубы) :

(1)

Коэффициент пропорциональности называется коэффициентом динамической вязкости. Так как градиент dw/dr отрицательный, то впереди поставлен знак минус. Выражение (1) называет­ся законом Ньютона. Закону Ньютона подчиняются маловязкие жидкос­ти, светлые нефтепродукты, легкие нефти, нефти с малым содержа­нием парафина, нефти с большим содержанием парафина при высоких температурах, высокосмолистые нефти также при высоких температурах.

Рис. 1. Зависимость напряжения сдвига τ от скорости сдвига dW/dr для различных жидкостей ( температура постоянная )

Кривые 2,3 и 4 (рис.1) характеризуют поведение неньютоновских жидкостей. Вязкость пластических (или бингамовских) жидкос­тей описывается уравнением Бингама :

. (2)

Из графика и уравнения (2) видно, что в этом случае движе­ние начинается только после того, как будет создано (преодолено) определенное (предельное) напряжение сдвига , после этого жидкость ведет себя как ньютоновская. Коэффициент пропорциональ­ности в этом случае называется коэффициентом пластической вязкос­ти. Предельное напряжение сдвига для круглой трубы определяется из условия равенства действующих сил на внутрен­ней поверхности:

.

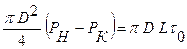Откуда (3)

,

где D и L - соответственно внутренний диаметр и длина трубопровода; P_Н и P_К - соответственно давление в начале и конце трубопровода;

Для псевдопластичных (кривая 3) и дилатантных жидкостей (кривая 4) в технических расчетах используется степенной закон изменения напряжения от скорости сдвига :

(4)

где k и n постоянные для данной жидкости коэффициенты, определяемые экспериментальным путем ;

- безразмерный модуль скорости сдвига.

Коэффициент n называют индексом течения, а k - характеристикой консистентности. Для псевдопластичных жидкостей n < 1, для дилатантных n> 1. Для ньютоновских жидкостей n = 1, а . Если начальный участок кривой -те­чения для псевдопластика мал, то расчет можно проводить по формуле (2), т.е. как для бингамовского пластика (пунктирная линия нарис. I); в этом случае (отрезок, отсекаемый на оси абс­цисс) физического смысла не имеет.

В зависимости от условий одна и та же жидкость ведет себя по разному. Например, парафинистые нефти и нефтепродукты при температурах, близких к температуре застывания и ниже, ведут се­бя как пластик бингама или псевдопластик, а при высоких темпера­турах- текут как ньютоновские жидкости. При высоких температурах основная часть парафина находится в растворенном состоянии, а в области низких температур в жидкой фазе имеются кристаллы пара­фина в свободном или связанном состоянии (образуют структуру).

Реологические характеристики парафинистых нефтей зависят также от времени. Так при механическом воздействии (встряхива­ние, перемешивание) система подвижна и течет, а при длительном покое (особенно при низких температурах) происходит ее застывание, образуется парафиновая структура, прочность которой возрастает во времени. Работа магистрального трубопровода неизбежно связа­на с остановками. И чем больше длительность остановки, тем большее давление необходимо создать для разрушения структуры в момент возобновления перекачки. Способность нефти с течением вре­мени восстанавливать разрушенную парафиновую структуру называет­ся тиксотропией. Ввиду множества факторов, влияющих на характе­ристики парафиновой структуры, не существует формул для расчета напряжений сдвига; в каждом конкретном случае его значение опре­деляется экспериментально (кривые течения строятся для различных условий, в первую очередь, для различных температур).

Движение реальной жидкости сопровождается потерей энергии, обусловленной вязкостью.

Поскольку существует несколько классов жидкостей, то опери­руют несколькими понятиями вязкости.

Для ньютоновской жидкости причиной потерь является не столь­ко трение о стенки трубопровода, сколько внутреннее трение жид­кости. Коэффициент динамической вязкости по кривой течения опре­деляется как

Коэффициенты динамической и кинематической вязкости связа­ны между собой плотностью ρ:

( 10 )

Плотность нефти при температуре Т может быть определена по формуле

, (11)

где - плотность нефти при температуре 293 К, кг/м³.

Расчетная плотность n нефтей с достаточной для практики точностью может быть определена

(12)

где - плотность i- й нефти обьемом V_i в общем случае V.

Расчетную плотность нефти для трубопровода большой протя­женности, проложенного в n климатических зонах, усредняют с учетом климатических поясов:

(13)

где 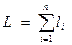- длина трубопровода;

-средняя плотность нефти на участке трубопровода длиной l_i с примерно одинаковой температу­рой.

Удельная теплоемкость С_р нефти изменяется в пределах 1600-2500 Дж/(кгК). При расчетах часто пользуются средним зна­чением Ср = 2100 Дж/(кгК). Для диапазона температур 273-673 К Ср можно вычислять по формуле Крего;

(14)

Коэффициент теплопроводности нефти изменяется в пределах 0,1 0,16. Обычно при расчетах используют среднее значение 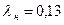Вт/(мк). Для более точных расчетов используют формулу Крего-Смита, справедливую для температур 273…473 K.

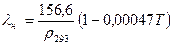(15)

Для трубопроводов большой протяженности, прокладываемых в нескольких климатических зонах, расчетные теплоемкость и коэф­фициент теплопроводности усредняют по длине, аналогично усред­нению плотности.

Если режим течения изотермический, то расчетные значения , С_р и принимают при среднемесячной температуре грунта (окружающей среды) самого холодно­го месяца на глубине заложения трубопровода (до оси) . Осреднение температуры грунта по длине трубопровода также производят по формуле (13) (вместо ; подставляю Т_0i ). При тепловых расчетах неизотермических потоков в трубопроводах температуру грунта осредняют аналогично. Конечно, можно и не производить усреднения параметров по длине, а делать все расчеты По каждой климатической зоне отдельно, согласовывая граничные условия. Но трудоемкость расчетов при этом возрастает в несколько раз.

1.2. Тепловой режим системы труба-грунт при перекачке подогретой нефти

Рассмотрим движение вязкой парафинистой нефти по трубопро­воду при неизотермическом установившемся режиме. Полагаем, что, если парафин кристаллизируется, то он уносится потоком, не осе­дая на стенках трубы.

В общем случае уравнение теплового баланса для элемента трубопровода длиной dx .отстоявшего на расстоянии x , будет

(16)

Первое слагаемое-это потери в окружающую среду с эле­мента трубопровода длиной dx (k - коэффициент теплопередачи; D - внутренний диаметр трубопровода; Т - температура неф­ти в трубопроводе на расстоянии X от начала; Т₀ - темпе­ратура окружающей среды (грунта), постоянная, осредненная по. длине)..

Второе слагаемое представляет собой теплоту трения в рас­сматриваемом сечении ( Q - объемный расход нефти . -плотность нефти, i - гидравлический уклон). Так как теплота трения час­тично компенсирует теплопотери, то перед вторым слагаемым постав­лен знак минус. .

Третье слагаемое-это тепло, выделяющееся при кристаллизации парафина (ε - массовое содержание парафина в нефти (в долях);χ - теплота кристаллизации; Т_нп и Т_нп - соответственно тем­пература начала и конца выпадения парафина). Тепло кристаллизации также частично компенсирует теплопотери в окружающую среду. Но, имея ввиду, что dT отрицательное ( температура по длине па­дает), то знак перед третьим слагаемым будет плюс (минус на ми­нус дает плюс).

В правой части уравнения теплового баланса записано измене­ние теплосодержания (С_р -теплоемкость нефти). Так как гра­диент отрицательный, то принят знак минус.

теплота трения ( b= 0 )

Характер изменения температуры по длине трубопровода для различных нефтей показан на рис.2. Видим, что самые высокие темпы снижения температуры присущи формуле Шухова. Тепло тре­ния и теплота кристаллизации снижают интенсивность охлаждения жидкости в трубопроводе.

Расчет теплового режима магистрального трубопровода являет­ся трудоемким, так как в общем случае могут быть участки, где парафин не выпадает ( Т_Н>Т_НП и Т >Т_КП) и где он выпадает ( Тнп≥Т ≥ Ткп)« В области высоких температур можно не учиты­вать теплоту трения, а при низких температурах она составляет значимую долю в тепловом балансе. Кроме этого, в трубопроводе могут быть два режима течения: на начальном участке, где темпе­ратуры высокие, возможен турбулентный режим течения, а на остав­шейся длине - ламинарный. Трудность расчета заключается в согла­совании условий на границах различных участков. Для упрощения изложения будем рассматривать случай наиболее интенсивного охлаждения, т.е. температура по длине трубопровода выражается формулой Шухова, при b = 0 ε =0 ;

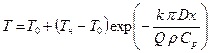( 19 )

Рис. 2. Изменение температуры нефти по длине трубопровода:

1 – по формуле Шухова , С^*_p = С_р , B = 0

2 – по формуле Лейбензона , ε = 0

3 – по формуле (18) , С^*_p > С_р ,ε ≠ 0 , B ≠ 0

4 – по формуле (18) , С^*_p > С_р ,ε ≠ 0 , B = 0

Рис. 3. Течение нефти в трубопроводе при двух режимах

Применяя ее к турбулентному участку, надо положить К= К_т:(см. рис.3). В конце турбулентного участка температура

( 20 )

где ; 0 ≤ X ≤ L ; T_н ≥ T ≥ T_кр (см. рис. 3 )

В конце трубопроводного участка температура

( 21 )

или

По аналогии для ламинарного участка можно записать (при К = К_л )

(22)

где ; L_Т ≤ x ≤ L ; T_кр ≥ T ≥ T_к

В конце ламинарного участка температура

(23)

или

На основании (21) и (23), исключая L_Т , можно получить соотношение, связывающее все граничные температуры в трубопро­воде с двумя режимами течения:

Критическую температуру Т_кр , соответствующую переходу турбулентного режима в ламинарный (и наоборот), определяют сле­дующим образом. Исходя из критического значения параметра Re ≈ 2000 , находим соответствующий ему коэффициент кинема­тической вязкости

(25)

Затем по вискограмме для данной нефти находим Т_кр . Ее можно найти и аналитически. Например» подставив в формулу (6) и Т_кр и решая совместно с (25), найдем

(26)

Используя другие аналитические зависимости для вязкости, можно найти соответствующие им формулы для Т_кр.

Коэффициент теплопередачи для трубопроводов зависит от внутреннего и внешнего коэффициентов тсплоотдатчи, а также от термического сопротивления стенки трубы, изоля­ции, отложений и т.п.

(27)

где D - внутренний диаметр трубопровода;

n - число слоев, учитываемых в термическом .сопротивле­нии при расчете;

коэффициенты теплопроводности слоев (отложений,стали трубы, изоляции и т.п.);

D_i , D_нi - соответственно внутренний и наружный диаметры каж­дого слоя;

D_н - наружный диаметр трубопровода (диаметр поверхности

соприкасающейся с грунтом).

Для определения при вынужденном движении жидкости имеются различные экспериментальные зависимости. Например, по Михееву

при ламинарном режиме (при Re ≤2 10³ )

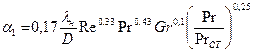(28)

при турбулентном режимеппри (Re ≥ 10⁴ )

(29)

где - параметр Грасгофа;

- параметр Прандтля;

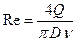- параметр Рейнольдса;

β_Т - коэффициент объемного расширения нефти.

Теплофизические характеристики в приведенных зависимостях определяются при средних температурах потока и стенки трубы (индекс „Ст" ), а за определяющий размер принят внутренний диаметр трубы. Теплофизические характеристики рассчитываются по формулам Крего.

В переходной области 2*10 3 ≤ Re ≤ 10 ⁴ внутренний коэффициент теплоотдачи , можно определять приближенно интерполяцией.

Для внешнего коэффициента теплоотдачи подземного трубопровода используют формулу Форхгеймера-Власова

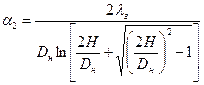, (30)

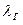- коэффициент теплопроводности грунта;

Н - глубина заложения трубопровода в грунт (до оси). При2Н/Дн > 2 (с погрешностью до I % )

(31)

При малых заглублениях ( H/D_H<3-4) пользуются формулой Аронса-Кутателадзе

(32)

где ;

Н_п- приведенная глубина укладки трубопровода, которая складывается из геометрической глубины заложения Н и эквивалентной глубины И_э ,определяемой по выраже нию

(33)

H _СН - толщина снежного покрова;

- коэффициент теплопроводности снега ( ≈ 0,105 Вт / (мK) -для свежее выпавшего снега; ≈ 0,465 Вт / (мK) - для уплотненного снега );

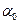- коэффициент теплоотдачи от поверхности грунта в воздух, при расчетах принимают 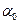≈ 11,63 Вт / (мK)

Для подземных и особенно теплоизолированных трубопроводов при турбулентном режиме течения >> , поэтому в большинст­ве случаев значением 1/ D в формуле (27) можно пренебречь. Для трубопроводов без специальной тепловой изоляции, прокладываемых в грунтах малой влажности, при турбулентном режиме течения с малой погрешностью можно принять К ≈ . При оценочных расче­тах коэффициент теплопередачи К принимают

для сухого песка 1,163 Вт/(м К),

для влажной глины 1,454 Вт/(м К),

для морского песка 3,489 Вт/(м К).

Расчет падения температуры можно выполнить более точно, если перегон разбить на отдельные участки в зависимости от грунтовых условий. Этот же расчет можно проводить по некоторому среднему значению . Падение температуры рассчитывают либо начиная с головного участка при известной начальной температуре подогрева, либо с конца участка при известной конечной температуре.

1.3. Потери напора на трение при перекачке подогретой нефти

С изменением температуры для нефтей отмечается наиболее существенное изменение вязкости (остальные параметры, как то плотность, теплоемкость, коэффициент теплопроводности можно принимать постоянными). При падении температуры по длине трубо­провода вязкость будет расти; следовательно, будет расти гидрав­лический уклон. Поэтому потери напора на трение при переменном гидравлическом уклоне следует вычислять как

Гидравлический уклон i выразим по Лейбензону:

,

где и m=1 –для ламинарного режима;

и m=0,25 -для турбулентного режима ( зона Блазиуса )

Другие зоны турбулентного режима течения при “горячих” перекач­ках маловероятны, так как требуются очень высокие температуры подогрева. С другой стороны, при высоких температурах вязкость (гидравлический уклон) практически остается постоянной и для определения h можно пользоваться формулами изотермического режима.

При перекачке подогретой нефти температура меняется и по длине и по радиусу трубопровода (в центре трубы жидкость имеет более высокую температуру, чем на стенке). Поэтому при вычисле­нии h необходимо учитывать и осевой и радиальный градиенты температур. Так как формулами (17... 24) определяется изменение средней по сечению температуры, то указанными зависимостями можно учесть осевой градиент температур. Влияние радиального гра­диента температур учтем по Михееву :

где ; ε_Р =0,9 – для ламинарного режима и ε_Р =1 для турбулентного режима

Тогда

Потери напора на трение в трубопроводе между тепловыми станциями при наличии двух режимов определяются как сумма

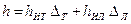( 35 )

где h_ИТ - потери на трение в трубопроводе на начальном турбулентном участке при условии T_Н = const ( изотермический режим при T_Н )

(36)

h_ИЛ - потери на трение в трубопроводе на конечном ламинарном участке при условии T_КР = const ( изотермический режим при T_КР )

(37)

- поправки на неизотермичность течения для турбулентного и ламинарного участков соответственно:

Для высокопарафинистых нефтей и нефтепродуктов, обладающих неньютоновскими свойствами, потери на трение приближенно можно определить по формуле Дарси - Вейсбаха

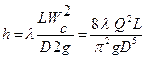, (40)

где W_С - средняя скорость перекачки.