
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Диэлектрическая проницаемость при очень больших частотах
В пределе функция стремится к единице. Это очевидно уже из простых физических соображений: при достаточно быстром изменении поля процессы поляризации, приводящие к установлению отличной от Е индукции D, вообще не успевают происходить.
Оказывается возможным установить справедливый для любых тел (безразлично — металлов или диэлектриков) предельный вид функции при больших частотах. Именно, частота поля должна быть велика по сравнению с частотами движения всех (или, по крайней мере, большинства) электронов в атомах данного вещества. При соблюдении этого условия можно при вычислении поляризации вещества рассматривать электроны как свободные, пренебрегая их взаимодействием друг с другом и с ядрами атомов.
Скорости v движения электронов в атомах малы по сравнению со скоростью света. Поэтому расстояния, проходимые ими в течение периода волны, малы по сравнению с длиной волны.
Ввиду этого при определении скорости, приобретаемой электроном в поле электромагнитной волны, можно считать последнее однородным.
Уравнение движения гласит:


где N — число электронов во всех атомах единицы объема вещества.

Фактическая область применимости этой формулы начинается от далекого ультрафиолета у самых легких элементов или от рентгеновских частот у более тяжелых элементов.
Вопрос23

| Хроматическая дисперсия состоит из материальной и волноводной составляющих и имеет место при распространении как в одномодовом, так и в многомодовом волокне. Однако наиболее отчетливо она проявляется в одномодовом волокне, в виду отсутствия межмодовой дисперсии.
Материальная дисперсия обусловлена зависимостью показателя преломления волокна от длины волны. В выражение для дисперсии одномодового волокна входит дифференциальная зависимость показателя преломления от длины волны.
 (2-18)
Волноводная дисперсия обусловлена зависимостью коэффициента распространения моды от длины волны [1] (2-18)
Волноводная дисперсия обусловлена зависимостью коэффициента распространения моды от длины волны [1]
 (2-19)
где введены коэффициенты M() и N() - удельные материальная и волноводная дисперсии соответственно, а (нм) - уширение длины волны вследствие некогерентности источника излучения. Результирующее значение коэффициента удельной хроматической дисперсии определяется как D() = M() + N(). Удельная дисперсия имеет размерность пс/(нм*км). Если коэффициент волноводной дисперсии всегда больше нуля, то коэффициент материальной дисперсии может быть как положительным, так и отрицательным. И здесь важным является то, что при определенной длине волны (примерно 1310 ± 10 нм для ступенчатого одномодового волокна) происходит взаимная компенсация M() и N(), а результирующая дисперсия D() обращается в нуль. Длина волны, при которой это происходит, называется длиной волны нулевой дисперсии 0. Обычно указывается некоторый диапазон длин волн, в пределах которых может варьироваться 0 для данного конкретного волокна.
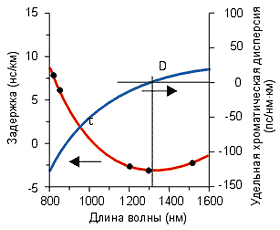
Фирма Corning использует следующий метод определения удельной хроматической дисперсии. Измеряются задержки по времени при распространении коротких импульсов света в волокне длиной не меньше 1 км. После получения выборки данных для нескольких длин волн из диапазона интерполяции (800-1600 нм для MMF, 1200-1600 нм для SF и DSF), делается повторная выборка измерения задержек на тех же длинах волн, но только на коротком эталонном волокне (длина 2м). Времена задержек, полученных на нем, вычитаются из соответствующих времен, полученных на длинном волокне, чтобы устранить систематическую составляющую ошибки.
Для одномодового ступенчатого и многомодового градиентного волокна используется эмпирическая формула Селмейера (Sellmeier, [4]): ) = A + B2 + C-2. Коэффициенты A, B, C являются подгоночными, и выбираются так, чтобы экспериментальные точки лучше ложились на кривую ), рис. 2.10. Тогда удельная хроматическая дисперсия вычисляется по формуле: (2-19)
где введены коэффициенты M() и N() - удельные материальная и волноводная дисперсии соответственно, а (нм) - уширение длины волны вследствие некогерентности источника излучения. Результирующее значение коэффициента удельной хроматической дисперсии определяется как D() = M() + N(). Удельная дисперсия имеет размерность пс/(нм*км). Если коэффициент волноводной дисперсии всегда больше нуля, то коэффициент материальной дисперсии может быть как положительным, так и отрицательным. И здесь важным является то, что при определенной длине волны (примерно 1310 ± 10 нм для ступенчатого одномодового волокна) происходит взаимная компенсация M() и N(), а результирующая дисперсия D() обращается в нуль. Длина волны, при которой это происходит, называется длиной волны нулевой дисперсии 0. Обычно указывается некоторый диапазон длин волн, в пределах которых может варьироваться 0 для данного конкретного волокна.
Фирма Corning использует следующий метод определения удельной хроматической дисперсии. Измеряются задержки по времени при распространении коротких импульсов света в волокне длиной не меньше 1 км. После получения выборки данных для нескольких длин волн из диапазона интерполяции (800-1600 нм для MMF, 1200-1600 нм для SF и DSF), делается повторная выборка измерения задержек на тех же длинах волн, но только на коротком эталонном волокне (длина 2м). Времена задержек, полученных на нем, вычитаются из соответствующих времен, полученных на длинном волокне, чтобы устранить систематическую составляющую ошибки.
Для одномодового ступенчатого и многомодового градиентного волокна используется эмпирическая формула Селмейера (Sellmeier, [4]): ) = A + B2 + C-2. Коэффициенты A, B, C являются подгоночными, и выбираются так, чтобы экспериментальные точки лучше ложились на кривую ), рис. 2.10. Тогда удельная хроматическая дисперсия вычисляется по формуле:
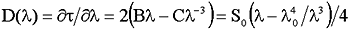 (2-20)
где 0 = (C/B)1/4 - длина волны нулевой дисперсии (zero dispersion wavelength), новый параметр S0 = 8B - наклон нулевой дисперсии (zero dispersion slope, его размерность пс/(нм2*км)), а - рабочая длина волны, для которой определяется удельная хроматическая дисперсия. (2-20)
где 0 = (C/B)1/4 - длина волны нулевой дисперсии (zero dispersion wavelength), новый параметр S0 = 8B - наклон нулевой дисперсии (zero dispersion slope, его размерность пс/(нм2*км)), а - рабочая длина волны, для которой определяется удельная хроматическая дисперсия.
Для волокна со смещенной дисперсией эмпирическая формула временных задержек записывается в виде ) = A + B + C ln, а соответствующая удельная дисперсия определяется как
со значениями параметров 0 = e-(1+B/C) и S0 = C/0, где - рабочая длина волны, 0 - длина волны нулевой дисперсии, и S0 - наклон нулевой дисперсии. Хроматическая дисперсия связана с удельной хроматической дисперсией простым соотношением chr() = D()·, где - ширина спектра излучения источника. К уменьшению хроматической дисперсии ведет использование более когерентных источников излучения, например лазерных передатчиков ( ~ 2 нм), и использование рабочей длины волны более близкой к длине волны нулевой дисперсии. В табл. 2.4 представлены дисперсионные свойства различных оптических волокон. |
Вопрос 24.
| Межмодовая дисперсия и полоса пропускания | |

| Межмодовая дисперсия возникает вследствие различной скорости распространения у мод, и имеет место только в многомодовом волокне (рис. 2.3 а, б). Для ступенчатого многомодового волокна и градиентного многомодового волокна с параболическим профилем показателя преломления (2-9) ее можно вычислить соответственно по формулам:
 (2-14) / (2-15),
где Lc - длина межмодовой связи (для ступенчатого волокна порядка 5 км, для градиентного - порядка 10 км).
Изменение закона дисперсии с линейного на квадратичный связано с неоднородностями, которые есть в реальном волокне. Эти неоднородности приводят к взаимодействию между модами, и перераспределению энергии внутри них. При L > Lc наступает установившийся режим, когда все моды в определенной установившейся пропорции присутствуют в излучении. Обычно длины линий связи между активными устройствами при использовании многомодового волокна не превосходят 2 км и значительно меньше длины межмодовой связи. Поэтому можно пользоваться линейным законом дисперсии.
Вследствие квадратичной зависимости от значения межмодовой дисперсии у градиентного волокна значительно меньше, чем у ступенчатого, что делает более предпочтительным использование градиентного многомодового волокна в линиях связи.
На практике, особенно при описании многомодового волокна, чаще пользуются термином полоса пропускания. При расчете полосы пропускания W можно пользоваться формулой [1]:
W = 0,44 /
(2-17)
Измеряется полоса пропускания в МГц*км. Из определения полосы пропускания видно, что дисперсия накладывает ограничения на дальность передачи и верхнюю частоту передаваемых сигналов. Физический смысл W - это максимальная частота модуляции передаваемого сигнала при длине линии 1 км. Если дисперсия линейно растет с ростом расстояния, то полоса пропускания обратно пропорционально зависит от расстояния. (2-14) / (2-15),
где Lc - длина межмодовой связи (для ступенчатого волокна порядка 5 км, для градиентного - порядка 10 км).
Изменение закона дисперсии с линейного на квадратичный связано с неоднородностями, которые есть в реальном волокне. Эти неоднородности приводят к взаимодействию между модами, и перераспределению энергии внутри них. При L > Lc наступает установившийся режим, когда все моды в определенной установившейся пропорции присутствуют в излучении. Обычно длины линий связи между активными устройствами при использовании многомодового волокна не превосходят 2 км и значительно меньше длины межмодовой связи. Поэтому можно пользоваться линейным законом дисперсии.
Вследствие квадратичной зависимости от значения межмодовой дисперсии у градиентного волокна значительно меньше, чем у ступенчатого, что делает более предпочтительным использование градиентного многомодового волокна в линиях связи.
На практике, особенно при описании многомодового волокна, чаще пользуются термином полоса пропускания. При расчете полосы пропускания W можно пользоваться формулой [1]:
W = 0,44 /
(2-17)
Измеряется полоса пропускания в МГц*км. Из определения полосы пропускания видно, что дисперсия накладывает ограничения на дальность передачи и верхнюю частоту передаваемых сигналов. Физический смысл W - это максимальная частота модуляции передаваемого сигнала при длине линии 1 км. Если дисперсия линейно растет с ростом расстояния, то полоса пропускания обратно пропорционально зависит от расстояния.
|
Вопрос 25
| Поляризационная модовая дисперсия | |

| Поляризационная модовая дисперсия pmd (polarization mode dispersion) возникает вследствие различной скорости распространения двух взаимно перпендикулярных поляризационных составляющих моды. Коэффициент удельной дисперсии T нормируется в расчете на 1 км и имеет размерность (пс/км1/2), а pmd растет с расстоянием по законуpmd=T·L1/2. Для учета вклада в результирующую дисперсию следует добавить слагаемое 2pmd в правую часть (2-13). Из-за небольшой величины pmd может проявляться исключительно в одномодовом волокне, причем когда используется передача широкополосного сигнала (полоса пропускания 2,4 Гбит/c и выше) с очень узкой спектральной полосой излучения 0,1 нм и меньше. В этом случае хроматическая дисперсия становится сравнимой с поляризационной модовой дисперсией.
В одномодовом волокне в действительности может распространяться не одна мода, а две фундаментальные моды - две перпендикулярные поляризации исходного сигнала. В идеальном волокне, в котором отсутствуют неоднородности по геометрии, две моды распространялись бы с одной и той же скоростью, рис. 2.11 а. Однако на практике волокна имеют не идеальную геометрию, что приводит к различной скорости распространения двух поляризационных составляющих мод, рис. 2.11 б.
 Рис. 2.11. Появление поляризационной модовой дисперсии [11]
Избыточный уровень pmd, проявляясь вместе с чирпированным модулированным сигналом от лазера, а также поляризационной зависимостью потерь, может приводить к временным колебаниям амплитуды аналогового видеосигнала. В результате ухудшается качество изображения, или появляются диагональные полосы на телевизионном экране. При передаче цифрового сигнала высокой полосы (>2,4 Гбит/с) из-за наличия pmd может возрастать битовая скорость появления ошибок.
Главной причиной возникновения поляризационной модовой дисперсии является некруглость (овальность) профиля сердцевины одномодового волокна, возникающая в процессе изготовления или эксплуатации волокна. При изготовлении волокна только строгий контроль позволяет достичь низких значений этого параметра.
Рис. 2.11. Появление поляризационной модовой дисперсии [11]
Избыточный уровень pmd, проявляясь вместе с чирпированным модулированным сигналом от лазера, а также поляризационной зависимостью потерь, может приводить к временным колебаниям амплитуды аналогового видеосигнала. В результате ухудшается качество изображения, или появляются диагональные полосы на телевизионном экране. При передаче цифрового сигнала высокой полосы (>2,4 Гбит/с) из-за наличия pmd может возрастать битовая скорость появления ошибок.
Главной причиной возникновения поляризационной модовой дисперсии является некруглость (овальность) профиля сердцевины одномодового волокна, возникающая в процессе изготовления или эксплуатации волокна. При изготовлении волокна только строгий контроль позволяет достичь низких значений этого параметра.
|
Вопрос 26
Дата добавления: 2015-01-29; просмотров: 362; Мы поможем в написании вашей работы!; Нарушение авторских прав |


 (2-21)
(2-21)