
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ (РАСПРЕДЕЛЕНИЕ ГАУССА)
Наибольшее распространение получил нормальный закон распределения, называемый часто распределением Гаусса:
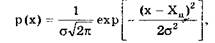 (6.6)
(6.6)
где σ — параметр рассеивания распределения, равный СКО; Хц — центр распределения, равный МО.
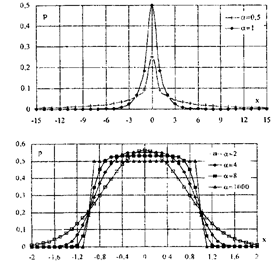
Рис. 6.6. Экспоненциальные распределения
Широкое использование нормального распределения на практике объясняется центральной предельной теоремой теории вероятностей, утверждающей, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.
Вид экспоненциальных распределений при различных значениях показателя а приведен на рис. 6.6.
При введении новой переменной t = (х-Хц)/σ из (6.6) получается нормированное нормальное распределение, интегральная и дифференциальная функции которого соответственно равны:
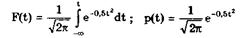
Нормирование приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения интегральной и дифференциальной функций нормированного нормального распределения сведены в таблицы, которые можно найти в литературе по теории вероятностей.
Определенный интеграл с переменным верхним пределом

называют функцией Лапласа.
Равномерное распределение. Непрерывная случайная величина Х называется равномерно распределенной на отрезке 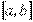 (a<b), если ее функция плотности распределения (рис. 1.6, а) имеет вид :
(a<b), если ее функция плотности распределения (рис. 1.6, а) имеет вид :
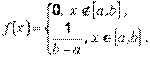
Соответственно функция распределения на отрезке  (рис. 1.6, б):
(рис. 1.6, б):
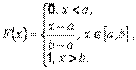
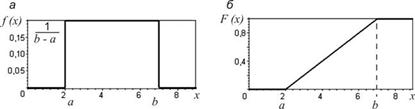
Рис. 1.6. Функции случайной величины, распределенной равномерно на [a,b]: а – плотности вероятностей f(x); б – распределения F(x)
Математическое ожидание и дисперсия данной СВ определяются выражениями:
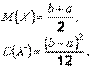
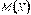 , в силу симметрии функции плотности, совпадает с медианой. Моды равномерное распределение не имеет.
, в силу симметрии функции плотности, совпадает с медианой. Моды равномерное распределение не имеет.
Показательное распределение. Распределение непрерывной случайной величины Х называется показательным (экспоненциальным), если плотность вероятности этой величины описывается функцией (рис. 1.7, а):
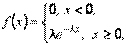
где λ – положительное число.
Соответственно функция распределения вероятностей имеет вид (рис. 1.7, б):
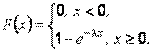

Рис. 1.7. Функции случайной величины, распределенной по показательному закону: а – плотности вероятностей f(x); б – распределения F(x)
Математическое ожидание и дисперсия равны соответственно
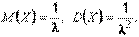
Распределение х2 . Сумма квадратов стандартных нормальных случайных величин имеет распределение, которое называется х2 -распределением с числом степеней свободы ν, равным числу независимых слагаемых в этой сумме [3]. Строгое определение требует указания плотности вероятности,
если 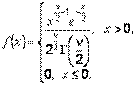
где  – число степеней свободы (число независимых слагаемых в используемой в знаменателе суммы квадратов);
– число степеней свободы (число независимых слагаемых в используемой в знаменателе суммы квадратов); 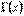 – гамма-функция, то случайная величина
– гамма-функция, то случайная величина 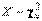 (рис. 1.9). Однако эта формула не столь наглядна, как формулы для равномерного и нормального распределений. Важно знать информацию, указанную в начале этого пункта, а также следующее: максимум плотности вероятности при
(рис. 1.9). Однако эта формула не столь наглядна, как формулы для равномерного и нормального распределений. Важно знать информацию, указанную в начале этого пункта, а также следующее: максимум плотности вероятности при 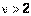 достигается при
достигается при  .
. 
Рис. 1.9. Функции плотности вероятностей c2-распределения с числом степеней свободы: а – ν = 1; б – ν = 3; в – ν = 10
Математическое ожидание и дисперсия равны соответственно: 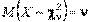
Распределение Стьюдента (t-распределение). Случайная величина  в виде отношения двух независимых случайных величин
в виде отношения двух независимых случайных величин  и
и 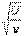 ,
, 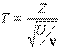 , где
, где 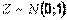 , а
, а 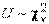 , имеет распределение Стьюдента
, имеет распределение Стьюдента
(t-распределение) с числом степеней свободы  . Функция плотности распределения имеет вид:
. Функция плотности распределения имеет вид:

Математическое ожидание и дисперсия 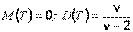
Распределение Фишера (Фишера-Снедекора, распределение дисперсионного отношения, F-распределение). Случайная величина 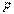 в виде отношения двух независимых случайных величин, распределенных как
в виде отношения двух независимых случайных величин, распределенных как 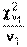 (числитель) и
(числитель) и 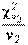 (знаменатель), имеет F-распределение с числами степеней свободы
(знаменатель), имеет F-распределение с числами степеней свободы  и
и 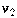 :
:
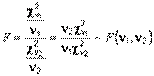
Иначе, случайная величина называется распределенной по F-распределению с параметрами 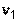 и
и  , если она имеет функцию плотности распределения
, если она имеет функцию плотности распределения
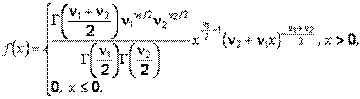
Математическое ожидание и дисперсия
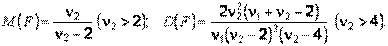
202. Какой закон распределения случайных погрешностей наиболее часто встречается в метрологии? Приведите его графическое изображение.
В практике электрических измерений одним из наиболее распространенных законов распределения случайных погрешностей является нормальный закон (Гаусса).
Математическое выражение нормального закона имеет вид

где f(D) – плотность вероятности случайной погрешности D = аi - A; s - среднее квадратическое отклонение. Среднее квадратическое отклонение может быть выражено через случайные отклонения результатов наблюдений Di (см. формулу Di = ai – A ):
σ=√((∆_1^2 )+∆_2^2+⋯+∆_n^2)/(n-1).
Характер кривых, описанных этим уравнением для двух значений s, показан на рис. 4.4. Из этих кривых видно, что чем меньше s, тем чаще встречаются малые случайные погрешности, т.е. тем точнее выполнены измерения. В практике измерений встречаются и другие законы распределения, которые могут быть установлены на основании статистической обработки.

203. Приведите уравнение закона нормального распределения?
См. вопрос №202
204. Что такое СКП случайной величины?
Средняя квадратическая погрешность (среднее квадратическое отклонение (Sд)) – характеристика рассеяния результатов измерений одной и той же величины вследствие влияния случайных погрешностей. Применяется для оценки точности первичных и вторичных эталонов. Она представляет среднюю квадратическую погрешность результата измерений, состоящую из случайных и неисключенных систематических погрешностей.
Наилучшим критерием оценки точности измерений принято считать среднюю квадратическую погрешность (СКП) измерения, определяемую по формуле Гаусса:
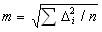
где Δi=li-X (Х - истинное значение измеряемой величины, а li - результат измерения).
Так как, в большинстве случаях истинное значение неизвестно, то СКП определяют по формуле Бесселя:
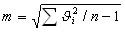
где ϑi=li-х (х - средняя арифметическое значение или вероятнейшее значение измеряемой величины, а li - результат измерения).
СКП арифметической середины:
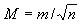
Эта формула показывает, что СКП арифметической середины в √n раз меньше СКП отдельного измерения.
205. Что характеризует СКП случайной величины?
Средняя квадратическая погрешность (среднее квадратическое отклонение (Sд)) – характеристика рассеяния результатов измерений одной и той же величины вследствие влияния случайных погрешностей. Применяется для оценки точности первичных и вторичных эталонов. Она представляет среднюю квадратическую погрешность результата измерений, состоящую из случайных и неисключенных систематических погрешностей.
206. Какие свойства закона нормального распределения вытекают из его симметричности?
График функции плотности f(x) симметричен относительно прямой, проходящей через точку а: х = а. Из этого свойства следует равенство для нормально распределенной случайной величины моды, медианы и математического ожидания.
207. Каким погрешностям соответствуют точки перегиба кривой нормального распределения?
208. Чему равна амплитуда кривой нормального распределения?
209. Какие погрешности при нормальном распределении считаются грубыми?
210. Как определить вероятность попадания случайной погрешности в симметричный интервал, при нормальном распределении?
211. Как определить вероятность попадания случайной погрешности в несимметричный интервал при нормальном распределении?
212. Как определит вероятность попадания случайной погрешности в несимметричный интервал при нормальном распределении и наличии систематической погрешности?
213. Что такое наблюдение при измерении?
Наблюдение при измерении - операции, проводимые при измерении и имеющие целью своевременно и правильно произвести отсчет.
214. Какие наблюдения называются равноточными?
Равноточные измерения — ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях с одинаковой тщательностью.
215. В чем отличие между СКП результатов наблюдений и СКП результата измерения?
216. Как вычисляется СКП результатов наблюдений?
217. Что характеризует СКП результатов наблюдении?
218. Как вычисляется СКП результата измерения?
219. Что характеризует СКП результата измерения?
220. Какому закону распределения всегда подчиняется среднее арифметическое? Почему?
221. Как можно определить характер закона распределения ряда наблюдений?
222. Какие критерии используют для проверки гипотезы о принадлежности результатов наблюдений нормальному распределению?
223. Как вычисляют доверительные границы случайной погрешности результата измерения при большом числе наблюдений (n>20) и нормальном распределении?
224. Как вычисляют доверительные границы случайной погрешности результата измерения при малом числе наблюдений (n<20)?
225. Как оценивают доверительные границы неисключенной систематической погрешности результата измерения?
226. Как вычисляют доверительные границы погрешности результата измерения?
Дата добавления: 2015-01-29; просмотров: 1240; Мы поможем в написании вашей работы!; Нарушение авторских прав |