Соединение нелинейных звеньев

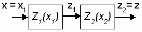
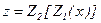
Одним из методов, позволяющих исследовать нелинейные системы, является метод фазовых траекторий, основополагающим понятием которого является фазовое пространство,т.е. такое пространство, в котором прямоугольными координатами точки являются величины, определяющие мгновенное состояние системы. Их называют фазовыми координатами.

Точка фазового пространства, соответствующая состоянию системы в данный момент времени, называется изображающей точкой. Изменение состояния системы во времени будет соответствовать движению изображающей точки в фазовом пространстве по определенной траектории, которая называется фазовой траекторией.

Лекция 14. Устойчивость нелинейных систем. Критерий Попова.

При исследовании устойчивости нелинейных систем исследуют отдельные виды движе-ния – состояние равновесия и автоколебания.

Одним из точных методов (критериев) анализа устойчивости нелинейных САР, не утративших свою актуальность и в настоящее время, является критерий абсолютной устойчивости В.М. Попова.

В этом критерии нелинейная САР условно разделена на чисто линейную часть, обычно расположенную в прямой цепи, и чисто нелинейную часть, обычно расположенную в цепи обратной связи (рис. 1).

В «классическом» варианте доказательства данного критерия принят ряд допущений:

1. Нелинейная часть – безинерционна.

2. Статическая характеристика нелинейной части является однозначной (без гистерезиса) и вписывается в Гурвицев угол К (0 < K < ).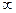

3. Линейная часть должна быть устойчивой, или в особых случаях иметь не более 2-х полюсов, расположенных на мнимой оси, при всех остальных полюсах передаточной функции, расположенных в левой полуплоскости.

4. В особых случаях должна иметь место предельная устойчивость.

В.М. Попов ввел понятие видоизмененной АФЧХ, обозначаемой обычно и определяемой соотношениями: ,

где 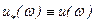; ; ; 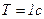, 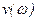– действительная и мнимая части АФЧХ линейной части, соответственно.

Существуют аналитическая и геометрическая формулировки абсолютной устойчивости по В.М. Попову. Более наглядной является геометрическая формулировка.

Для того, чтобы имела место абсолютная устойчивость в угле [0; К] в основном и в угле [eps; К] (где eps – бесконечно малое положительное число) в особых случаях, достаточно, чтобы в плоскости можно было выбрать прямую, проходящую через точку действительной оси с абсциссой –1/K так, чтобы годограф весь лежал строго справа от этой прямой и чтобы, кроме того, в особых случаях имела место предельная устойчивость.

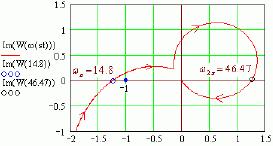
На рис. 2 представлена графическая иллюстрация критерия Попова при анализе устойчивости нелинейной САР, где пунктирной линией представлен традиционный годограф Найквиста (годограф АФЧХ) для линейной части САР (W_лин), сплошной линией представлен видоизмененный годограф Попова, а точка на оси абсцисс с координатой -1/K (K – Гурвицев угол) расположена левее точки пересечения годографа Попова с осью абсцисс.

Очевидно, что через точку -1/К можно провести бесчисленное множество прямых.

На рис. 2 одна из множества прямых проведена так, что видоизмененный годограф Попова лежит строго справа от этой прямой.

Резюме: нелинейная САР абсолютно устойчива.

Следует отметить, что условие устойчивости, вытекаю-щее из критерия устойчивости Попова, являются достаточным, но не необходимым.

Иными словами: если выполняются условия критерия Попова, то система гарантировано устойчива. Но, если условие Попова не выполняется, то система может быть как устойчива, так и неустойчива.

Лекция 15. Импульсные САУ.

Импульсными называются САУ, в которых наряду с непрерывными действуют ипульсно-модулированные сигналы. Импульсно-модулированные сигналы представляют собой последовательность импульсов, у которых один или несколько параметров меняются по определенному временному закону. Такими параметрами являются:

- амплитуда импульсов;

- длительность импульса;

- период повторения импульсов.

Импульсный элемент это элемент, который преобразует непрерывный сигнал в дискретный, т.е. в последовательность коротких импульсов, амплитуда (или площадь) которых пропорциональна текущему значению величины непрерывного сигнала.

Квантование (по уровню) это приближенная замена непрерывно изменяющегося во времени сигнала ступенчатой последовательностью.Как только непрерывный сигнал достигает некоторого, заранее заданного уровня из набора возможных, квантованному сигналу присваивается значение этого уровня:

Шаг квантования – разность значений соседних уровней квантования. Величина шага определяет точность аппроксимации исходного сигнала. Шаг может быть фиксированным или зависеть от уровня. Часто бывает достаточно 8 – 16, реже 256 уровней во всем диапазоне изменения исходного сигнала. В некоторых случаях бывает достаточно всего трех уровней ( ).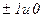

Достоинство квантования: возможность замены непрерывного сигнала последовательностью чисел, соответствующих уровням квантования в некоторые моменты времени. Отсюда высокая помехозащищенность при передаче по каналам с шумами. Вместо передачи самого сигнала можно передавать соответствующее текущему значению число в двоичной форме. Это и дает высокий выигрыш в помехозащищенности.

Недостаток– изменение уровня квантования происходит в произвольные моменты времени. Кроме того, квантование сопровождается ошибками, которые могут быть минимизированы уменьшением шага квантования.

Дискретизация (по времени) это преобразование непрерывногосигнала в последовательность коротких импульсов, с амплитудой(или шире, с другим параметром, например площадью или шириной импульса), равной значению сигнала в моменты стробирования, т.е. считывания значения непрерывного сигнала. Качество представления непрерывного сигнала амплитудным дискретным определяется частотой стробирования (отсчитывания значений) непрерывного сигнала: чем выше частота, тем выше качество.

Достоинство совместной дискретизации и квантования в том, что непрерывный сигнал можно заменить последовательностью следующих друг за другом через равные промежутки времени чисел. Их удобно хранить на компьютерных носителях, обрабатывать на числовых процессорах и передавать по линиям связи с высокой надежностью.

Теорема Котельникова определяет частоту стробирования (считывания) непрерывного сигнала с ограниченным спектром, такую, при которой непрерывный сигнал может быть совершенно точно восстановлен по амплитудам, импульсов считанным с частотой Котельникова – частота дискретизации должна быть не менее чем вдвое выше самой верхней частоты спектра 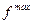дискретизируемого сигнала ( ).

Иллюстрация возможных вариантов дискретизации

Лекция 16. Автоколебательные системы.

В учебниках по ТАУ, в отличие от учебников по электронике, теории цепей и некоторым другим предметам, обычно не рассматривается физический смысл механизма, приводящего к неограниченному возрастанию амплитуды колебаний на выходе неустойчивой САР. Неустойчивая САР при этом превращается в автоколебательную. Чтобы восполнить этот пробел, рассмотрим процессы, происходящие в контуре неустойчивой САР.

Пусть имеется САР с управлением по отклонению:

Возникновение на выходе неустойчивой САР колебаний с возрастающей амплитудой, и частотой, примерно равной частоте 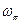, обусловлено тем, что возвращаемая обратной связью и инвертируемая сумматором синусоида частоты 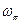совпадает по фазе с входным сигналом звена прямой связи САР. Действительно, синусоида частоты 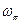задерживается по фазе в звене прямой связи на угол , да еще инвертирование в сумматоре следует рассматривать как дополнительную задержку на , что дает в итоге задержку на . Кроме того, проходя очередной раз контур, синусоида усиливается звеном прямой связи (в рассматриваемом примере в 1.2 раза). Этот своеобразный резонанс с подкачкой энергии в звене прямой связи и ведет к возрастанию амплитуды колебаний частоты 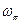по экспоненциальному закону.

Колебания с частотой, отличающейся от частоты 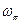, ввиду того, что они возвращаются с выхода САР на вход звена прямой связи не в фазе, в конечном итоге подавляются. Поэтому из всего спектра входного сигнала, в данном случае ступенчатой функции, неустойчивой системой выделяется и развивается в дальнейшем только компонента с частотой 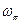. Ответ на вопрос: «Откуда взялась на входе звена прямой связи синусоида частоты ωπ?» прост. Такая компонента есть в непрерывном спектре ступеньки. Но даже если не подавать на вход реальной САР никаких сигналов, то и в этом случае возникнут и начнут развиваться колебания выходной величины. Дело в том, что в реальности существуют шумы различной природы. Они есть и на входе звена прямой связи. В спектре шумов имеется и, пусть малая по величине, компонента с частотой .

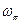Физический механизм развития колебаний может рассматриваться как резонанс, при котором в процессе этих колебаний добавляется энергия большая, чем теряется на трение. Это

эквивалентно колебательному звену с отрицательным декрементом затухания.

Отрицательный декремент физически означает превышение поступающей в систему энергии над энергией, рассеиваемой в течение периода колебаний.

Из проведенного рассмотрения следует, что для возникновения в контуре САР колебаний с возрастающей амплитудой требуется, чтобы хотя бы на одной частоте были выполнены условия:

- контурное усиление превышает 1;

- фазовая задержка в контуре с учетом инвертирования сигнала в сумматоре кратна .

В устойчивой САР эти условия одновременно не выполняются. Контурное усиление на частоте 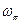меньше 1, что и приводит к затуханию колебаний, если они возникают в переходном процессе.