Движение неньютоновских жидкостей в трубах

При движении вязкой ньютоновской жидкости по круглой трубе в соответствии с законом вязкого трения Ньютона (1.9) касательное напряжение t пропорционально градиенту скорости и(r ), т.е.

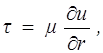(10.1)

где r — текущий радиус.

Величина h = ¶ u/¶ r называется скоростью сдвига и уравнение (10.1) записывается в виде

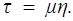(10.2)

При этом считается, что при температуре Т = const динамический коэффициент вязкости m = const.

Уравнение (10.2) представляет собой простейший пример реологи­ческого уравнения жидкости. Это уравнение содержит единственный реологический параметр - динамический коэффициент вязкости. Наи­более простой классификацией неньютоновских жидкостей является классификация, в которой неньютоновские жидкости группируются по трем основным категориям.

1. Неньютоновские вязкие жидкости, для которых скорость сдвига зависит только от приложенных напряжений, т.е.

h = f(t). (10.3)

2. Жидкости, для которых скорость сдвига определяется не только величиной касательного напряжения, но и продолжительностью его действия.

3. Вязкоупругие жидкости, проявляющие одновременно вязкость и упругость.

Неньютоновские вязкие жидкости делятся на две группы:

а) жидкости, обладающие начальным напряжением сдвига t₀, т.е. жидкости, которые начинают течь лишь после того, как каса­тельное напряжение превысит некоторый предел t₀;

б) жидкости, не обладающие начальным напряжением сдви­га t₀.

Примером жидкости группы а) является вязкопластичная жид­кость. Ее реологическое уравнение имеет вид

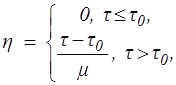(10.4)

т.е. при t £ t₀ среда ведет себя как твердое тело.

Величина m называется коэффициентом пластической вязкости.

Примером жидкостей группы б) являются степенные или нелиней­но-вязкие жидкости. Их реологическое уравнение имеет вид

t = k hⁿ,

где k — консистентность; n —индекс течения.

Зависимость касательного напряжения от скорости сдвига называет­ся кривой течения.

Кривые течения степенных жидкостей проходят через начало коор­динат. При п < 1 жидкость называется псевдопластичной, а при п > 1 - дилатантной.

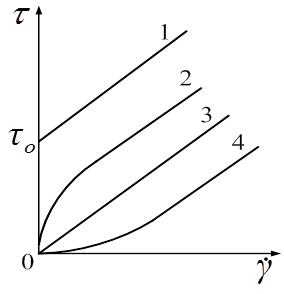
Рис. 10.1. Кривые течения неньютоновских вязких жидкостей

На рис. 10.1 приведены кривые течения неньютоновских вязких жидкостей. Кривая 1 соответствует вязкопластичной жидкости, кривая 2 —псевдопластичной, кривая 4 —дилатантной; кривая 3 соответствует случаю п = 1, т.е. представляет собой кривую течения для вязкой жид­кости.

Для неньютоновских вязких жидкостей вводится понятие кажу­щейся вязкости

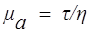(10.5)

и текучести

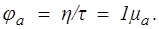(10.6)

В отличие от ньютоновской жидкости величины m_а и j_а — не конс­танты, а функции касательного напряжения.

При движении неньютоновской вязкой жидкости по трубе радиусом а и длиной l под действием перепада давления Dp распределение каса­тельного напряжения по радиусу, как и в случае ньютоновской жидкос­ти, имеет вид

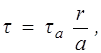(10.7)

где t_а — касательное напряжение на стенке трубы, определяемое из соотношения:

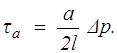
Распределение скорости по сечению трубы определяется по формуле

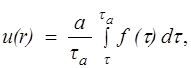(10.8)

где f(t) определяется по формуле (10.3).

Расход неньютоновской вязкой жидкости определяется при любом виде функции f(t) из соотношения

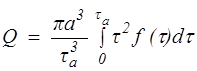. (10.9)

Формулы (10.6) и (10.7) справедливы при отсутствии пристенного скольжения. При вращательном течении неньютоновской вязкой жид­кости между двумя соосными цилиндрами распределение касательного напряжения по радиусу имеет вид

(10.10)

где М — момент сил трения, действующих на единицу длины цилиндра.

Угловая скорость наружного цилиндра W при отсутствии пристен­ного скольжения и неподвижном внутреннем цилиндре определяется по формуле

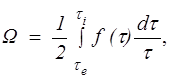(10.11)

где t_i , t_e — напряжения сил трения на поверхностях внутреннего и наружного цилиндра соответственно.

Вопросы по теме 10.

1. Как определяется неньютоновская жидкость?

2. Какая жидкость называется неньютоновской вязкой?

3. Каким реологическим уравнением описывается течение вязко-пластичной жидкости?

4. Сколько реологических параметров определяют модель степенной жидкости?

5. Как распределяется касательное напряжение по радиусу кольце­вого зазора при вращательном течении жидкости?

6. К каким особенностям в распределении скорости по сечению тру­бы приводит наличие начального напряжения сдвига в модели вязко-пластичной жидкости?