Приборы для измерения давления. 1) Пьезометр – простейшее устройство для измерения давления (рис

1) Пьезометр – простейшее устройство для измерения давления (рис. 2.9). Представляет собой вертикальную стеклянную трубку, верхний конец которой открыт в атмосферу, а нижний присоединён к ёмкости, в которой измеряется давление. По пьезометру можно определить пьезометрическую высоту, равную , представляющую собой высоту столба жидкости, соответствующую данному давлению Р (абсолютному или избыточному).

, где

Р_абс. – абсолютное давление в жидкости на уровне присоединения пьезометра; Р_а – атмосферное давление.

Отсюда, высота подъёма жидкости в пьезометре:

, где

Р_изб. – избыточное давление на уровне присоединения пьезометра.

Если на свободную поверхность покоящейся жидкости действует атмосферное давление, то пьезометрическая высота для любой точки рассматриваемого объёма жидкости равна глубине расположения этой точки.

Простейшим устройством для измерения вакуума может служить стеклянная трубка, показанная на рис.2.6 в двух вариантах. Вакуум в жидкости А можно измерять при помощи U-образной трубки или перевёрнутой U-образной трубки, один конец которой опущен в сосуд с жидкостью.

Для измерения давления жидкостей и газов в лабораторных условиях помимо пьезометра пользуются жидкостными и механическими манометрами (рис.2.11).

Так называемый U-образный манометр (рис.2.11.а) представляет собой изогнутую стеклянную трубку, содержащую ртуть. При измерении наибольших давлений газа вместо ртути применяют спирт, воду и иногда тетрабромэтан (ρ=2,95).

Рис.2.9. Пьезометр, присоединённый к баку

Рис.2.10. Простейшие вакууметры

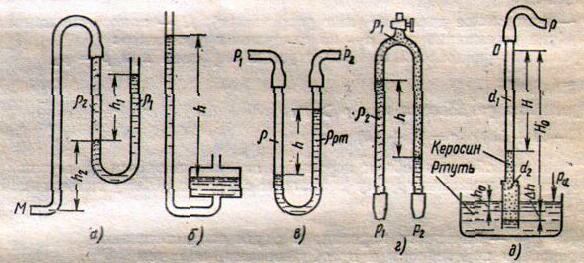
Рис. 2.11. Схемы жидкостных манометров

Если измеряется давление жидкости в точке М, и соединительная трубка заполнена этой же жидкостью, то следует учитывать высоту расположения манометра над точкой М. Так, избыточное давление в точке М:

Чашечный манометр (рис.2.11,б) удобнее описанного выше тем, что при пользовании им необходимо фиксировать положение лишь одного уровня жидкости (при достаточно большом диаметре чашки по сравнению с диаметром трубки уровень жидкости в чашке можно считать неизменным).

Для измерения разности давлений в двух точках служат дифференциальные манометры, простейший из которых - U-образный манометр показан на рис.2.11,в. Если при помощи такого манометра, обычно заполняемого ртутью, измерена разность давлений Р₁ и Р₂ в жидкости плотностью ρ,которая полностью заполняет соединительные трубки, то:

Для измерения малых перепадов давления воды применяют двухжидкостный микроманометр, представляющий собой перевёрнутую U-образную трубку с маслом или керосином в верхней части (рис.2.11,г). Для этого случая:

Двухжидкостный чашечный манометр (рис.2.11,д) предназначен для измерения давлений или разрежений воздуха в интервале от 0,01 до 0,05 МПа, когда спиртовой или водяной манометр даёт чрезмерно высокий столб спирта или воды, а потому неудобен для пользования, а ртутный манометр не даёт необходимой точности из-за недостаточной высоты столба ртути. Таким манометром, например, пользуются при опытах в скоростных аэродинамических трубах. В чашке – ртуть, в трубке – спирт, керосин или иная жидкость. Соответствующим подбором диаметров верхнего d₁ и нижнего d₂ участков трубки можно получить любую условную плотность ρ_усл. ,входящую в формулу Р = Hρ_усл.g , где Р– измеряемое давление (или разряжение); Н – показание манометра.

Наряду с механическими манометрами применяют электрические манометры. В качестве чувствительного элемента (датчика) в электроманометре используют мембрану. Под действием измеряемого давления мембрана деформируется и через передаточный механизм перемещает движок потенциометра.

Иллюстрации к Лекции 3: ОСНОВЫ ГИДРОДИНАМИКИ

Гидродинамика - раздел гидравлики, в котором изучаются законы движения жидкости и её взаимодействие с неподвижными и подвижными поверхностями.

Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения.

Рис. 3.1. Живые сечения: а - трубы, б - клапана

Смоченный периметр χ("хи") - часть периметра живого сечения, ограниченное твердыми стенками (рис.3.2, выделен утолщенной линией)

Рис. 3.2. Смоченный периметр

Средняя скорость потока υ - скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω:

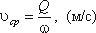
Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной. Трубка тока - трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока, называется элементарной струйкой.

Рис.3.4. Труба с переменным диаметром при постоянном расходе

Рис.3.5. Схема к выводу уравнения Бернулли для идеальной жидкости

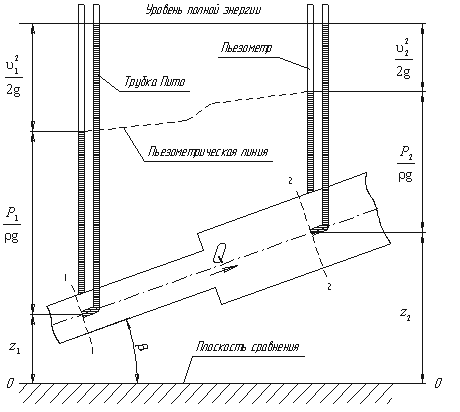
Рис.3.6. Схема к выводу уравнения Бернулли для реальной жидкости

Рис. 3.7. Трубка Пито и

pасходомер

Вентури

Иллюстрации к Лекции 4: ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ

Рис. 4.1. Схема установки Рейнольдса

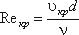
где ν - кинематическая вязкость; - скорость потока жидкости; d- внутренний диаметр трубы.

Рис. 4.2. Схема трубки для демонстрации кавитации

Рис. 4.3. Схема для рассмотрения ламинарного потока

-

формула Вейсбаха-Дарси,

где λ - коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению: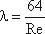

При ламинарном режиме для определения коэффициента гидравлического трения λ Т.М. Башта рекомендует при Re < 2300 применять формулу: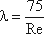

Рис. 4.6. Модель турбулентного режима движения жидкости

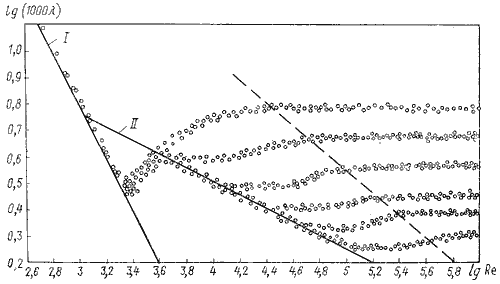
Рис. 4.7. График Никурадзе

Табл. 4.8

Таблица для

определения коэффи-

циента гидравличес-кого трения

Рис. 4.9. Номограмма Колбрука-Уайта для определения коэффициента гидравлического трения

Рис. 4.9. Внезапное расширение трубы

Рис. 4.10. Постепенное расширение трубы

Рис. 4.11. Внезапное сужение трубы

Рис. 4.12. Конфузор Рис. 4.13. Сопло

ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ, НАСАДКОВ

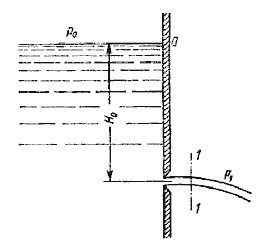
Рис. 5.1. Истечение из резервуара через малое отверстие

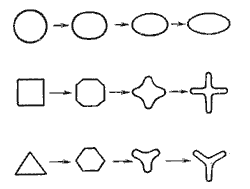
Рис. 5.2. Истечение через круглое отверстие

Несовершенное сжатие наблюдается в том случае, когда на истечение жидкости через отверстие и на формирование струи оказывает влияние близость боковых стенок резервуара (рис.5.5).

Рис. 5.5. Схема несовершенного сжатия струи

Рис. 5.6. Истечение под уровень

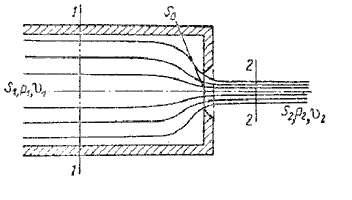
Рис. 5.7. Истечение через насадок

Рис. 5.8. Истечение жидкости через насадки: а - расширяющиеся конические; б - сужающиеся конические;

в - коноидальные; г - внутренние цилиндрические

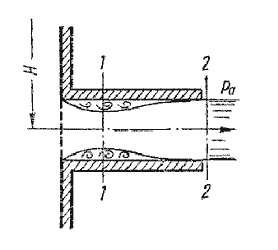
Рис. 5.10. Истечение из-под затвора через незатопленное отверстие

Рис. 5.11. Взаимодействие струи жидкости с неподвижной поверхностью

Рис. 5.12. Составные части

свободной струи

РАСЧЕТ ПРОСТЫХ ТРУБОПРОВОДОВ

Рис. 6.1. Схема простого трубопровода

Рис.6.2. Зависимости потребных напоров от расхода жидкости в трубопроводе

Рис. 6.3. Последовательное соединение трубопроводов

Рис. 6.4. Параллельное соединение трубопроводов

Разветвлённым соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение - место разветвления (или смыкания) труб.

Рис. 6.5.

Разветвленный трубопровод

Рис. 6.6. Схемы сложных трубопроводов

трубопровода

Рис. 6.8. Трубопроводы

с насосной подачей жидкости

Рис. 6.9. Графическое нахождение рабочей точки

Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока рабочей жидкости.

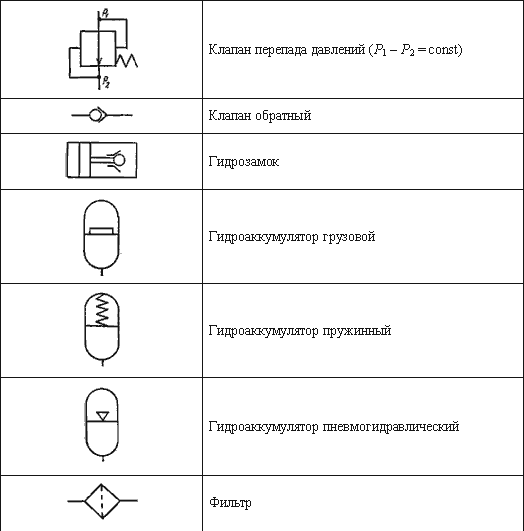
Таблица 6.11. Условные обозначения основных гидроэлементов