
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет всасывающей магистрали.
Диаметр трубопровода всасывающей магистрали 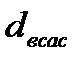 , м равен диаметру первого участка сети
, м равен диаметру первого участка сети 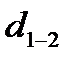 , м или диаметру всасывающей магистрали насоса
, м или диаметру всасывающей магистрали насоса  , м.
, м.
Потери напора во всасывающей магистрали  , м определяется формулой:
, м определяется формулой:
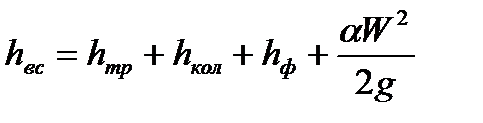 , (1.8)
, (1.8)
где 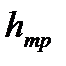 - потери на трение, м;
- потери на трение, м;
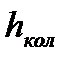 - потери в колене, м;
- потери в колене, м;
 - потери на фильтре, м;
- потери на фильтре, м;
α – коэффициент Дарси (α =1,05);
W – скорость воды во всасывающей магистрали.
Потери на трение 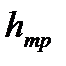 , м определим по формуле (1.2):
, м определим по формуле (1.2):
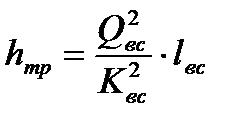 ,
,
где 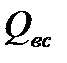 - расход воды во всасывающей магистрали (
- расход воды во всасывающей магистрали ( 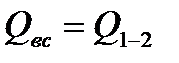 );
);
 - квадрат модуля расхода для трубы, всасывающей магистрали;
- квадрат модуля расхода для трубы, всасывающей магистрали;
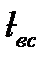 - длина всасывающей магистрали, м.
- длина всасывающей магистрали, м.
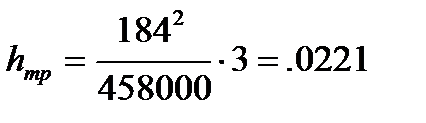 м,
м,
2) Потери в колене 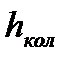 , определим по формуле Вейсбаха:
, определим по формуле Вейсбаха:
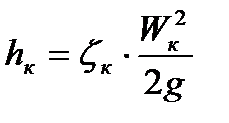 , (1.9)
, (1.9)
где 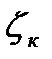 - коэффициент местного сопротивления колена. Определяется из таблицы 4;
- коэффициент местного сопротивления колена. Определяется из таблицы 4;
Колена Таблица 4
| Вид | а | б | в | г |
| ζк | 4,01 | 4,51 | 2,705 | 0,996 |
| а) |
| б) |
| в) |
| г) |
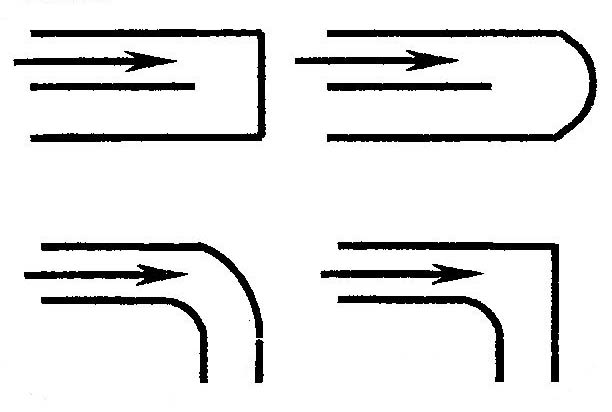
Рис 1.2. Колена.
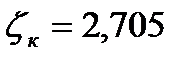 (определяем из таблицы 4).
(определяем из таблицы 4).
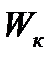 - скорость воды в колене, м/с. Определяется из уравнения неразрывности (1.2):
- скорость воды в колене, м/с. Определяется из уравнения неразрывности (1.2):
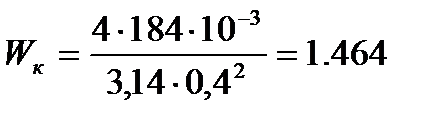 м/с.
м/с.
Подставляем полученные значения скорости воды в колене и коэффициента местного сопротивления колена в формулу Вейсбаха:
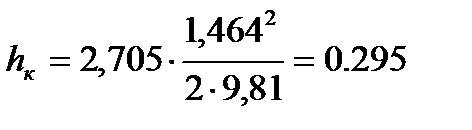 м.
м.
Определяем потери в фильтре:
| 3d |
| 2d |
Рис. 1.3. Фильтр
Коэффициент местного сопротивления фильтра 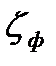 :
:
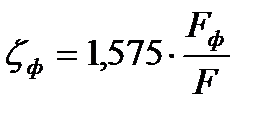 , (1.10)
, (1.10)
где Fф – площадь фильтра, м2;
F – суммарная площадь отверстий фильтра, м2.
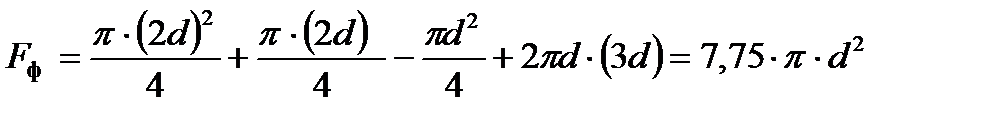 ,
,
 м2.
м2.
Определим площадь отверстий фильтра F, м2;
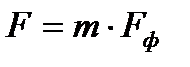 ,
,
где 
a – размер ячейки сетки фильтра в «свету» а = 5мм;
t – размер ячейки сетки фильтра по осям t = 6мм (шаг сетки);
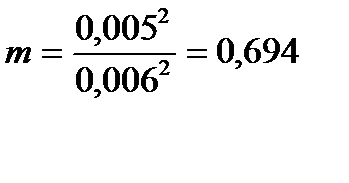
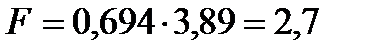 м2.
м2.
Рассчитываем коэффициент местного сопротивления фильтра 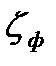 :
:
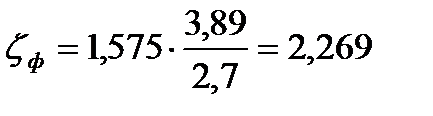 .
.
Определим скорость воды в фильтре 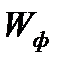 , м/с по уравнению:
, м/с по уравнению:
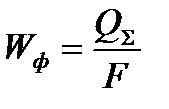 ,
,
где 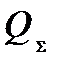 - суммарный расход воды, м3;
- суммарный расход воды, м3;
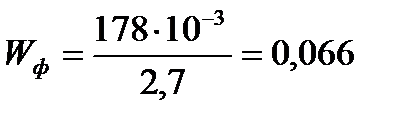 м/с.
м/с.
Потери на фильтре 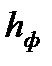 , определяем по формуле Вейсбаха:
, определяем по формуле Вейсбаха:
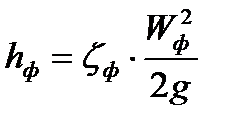 ,
,
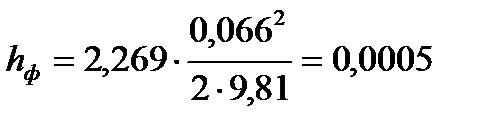 м.
м.
4) Потери напора во всасывающей магистрали  , м:
, м:
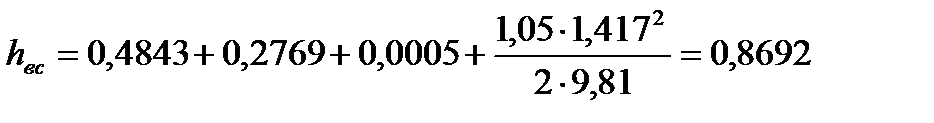 м.
м.
Дата добавления: 2015-04-18; просмотров: 311; Мы поможем в написании вашей работы!; Нарушение авторских прав |