ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Гидродинамикой называется раздел гидравлики, в котором изучают законы движения жидкости. Для выполнения гидродинамических расчетов применяют уравнение неразрывности потока, которое является первым основным уравнением гидродинамики. Уравнение неразрывности потока связывает такие величины как средняя скорость потока и расход.

Расходом называется количество жидкости, протекающее через живое сечение потока (струйки) в единицу времени. Это ко­личество можно измерять в единицах объема, веса и массы, по­этому различают расходы: объемный Q, 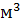/с; весовой , Н/с; массовый Qm, кг/с.

Объемный расход жидкости:

Q= V/t, (44)

где V - объем жидкости, 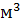; t - время, с.

Весовой расход жидкости

= mg/t, (45)

где m - масса жидкости, кг; g - ускорение свободного падения, равное 9,81 м/с2.

Массовый расход жидкости

Qm = m/t (46)

Между весовым и объемным расходами жидкости существует следующая зависимость:

= pgQ. (47)

Средняя скорость потока , м/с, определяется как объемный расход жидкости через единицу живого сечения потока:

= Q/ω. (48)

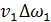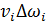= = = = const (49)

Произведение площади поперечного сечения труб­ки тока и скорости течения несжимаемой жидкости есть величина постоянная для данной трубки тока. Так формулируется теорема о неразрывности струи, а уравнение (49) называется уравнением постоянства объемного расхода элементарной струйки.

Для потока конечных размеров

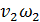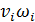= = = = const

Из уравнения (49) следует

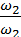= (50)

т. е. средние скорости в потоке несжимаемой жидкости обратно пропорциональны площади живых сечений.

Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее зависимость между скоростью и давлением в различных сечениях одной и той же струйки.

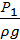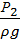+ + = + + (51)

z + + 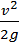= const (52)

Для потока реальной жидкости уравнение Бернулли имеет вид:

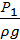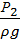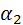
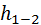+ + = + + + (53)