
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример. Выполнить гидравлический расчет трубопровода, схема которого прилагается.
Выполнить гидравлический расчет трубопровода, схема которого прилагается.
Данную схему можно разбить на 4 простых трубопровода, причем трубопровод l1d1 является всасывающим и рассчитывается отдельно от сложного трубопровода, состоящего из трубы 2 (l2d2), трубы 3 (l3d3) и трубы 4 (l4d4).
Составим уравнение Бернулли для трубопровода 1, относительно плоскости отсчета, проведенной через свободную поверхность жидкости в первом резервуаре. При этом начальное сечение соответствует свободной поверхности жидкости в первом резервуаре, а конечное сечение – на входе в насос.
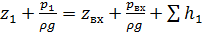 , (1)
, (1)
где z1 – высотная отметка начального сечения;
р1 – избыточное давление на свободной поверхности в первом резервуаре;
zвх – высотная отметка входа в насос;
рвх – избыточное давление на входе в насос;
Σh1 – суммарные потери напора в первом трубопроводе.
Это уравнение позволяет определить рвх при известном расходе или, при известном рвх, определить расход (задача второго типа на расчет простого трубопровода).
Если, по заданным условиям, неизвестными являются и рвх и расход Q, то тогда нужно в первую очередь определить расход Q, выполнив предварительно расчет разветвленной части трубопровода, и, зная Q, определить рвх из уравнения (1).
Составим систему уравнений Бернулли и уравнений расходов для разветвленной части трубопроводной сети.
Для трубопровода 2:
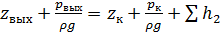 ,
,
Обозначая 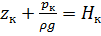 , преобразуем уравнение к виду:
, преобразуем уравнение к виду:
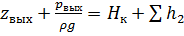 ,
,
или
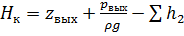 . (2)
. (2)
Для трубопровода 3:
 . (3)
. (3)
Для трубопровода 4:
 . (4)
. (4)
Уравнения расходов:
Q1 = Q2 = Q
Q = Q3 + Q4 (5)
Полученные уравнения сведем в систему:

Для решения полученной системы уравнений рассчитаем гидравлические характеристики каждого трубопровода.
Если известен общий расход Q в системе, то задаваясь значениями расходов от нуля до ≈ 1,2Q, рассчитаем потери напора в каждой из труб по формуле Дарси-Вейсбаха:
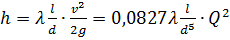 (6)
(6)
Для каждого значения расхода Q рассчитываем число Рейнольдса:
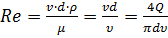 ,
,
где ρ – плотность жидкости,
v – средняя скорость движения,
d – диаметр трубопровода,
μ – динамическая вязкость,
υ – кинематическая вязкость.
Сравнивая полученное число Рейнольдса с критическим Reкр = 2320 и граничными (переходными) числами  и
и 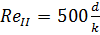 , определяем режим движения (ламинарный или турбулентный) и, в случае турбулентного режима, зону гидравлического сопротивления (гладких труб, смешанного трения, шероховатых труб).
, определяем режим движения (ламинарный или турбулентный) и, в случае турбулентного режима, зону гидравлического сопротивления (гладких труб, смешанного трения, шероховатых труб).
Далее выбираем формулу для расчета коэффициента гидравлического сопротивления λ:
- если рассчитанное число Рейнольдса Re < Reкр = 2320, то режим движения ламинарный, и λ определяем по формуле Стокса:
 ;
;
- если Reкр < Re < ReI, то режим движения турбулентный, зона гидравлически гладких труб, и λ определяем по формуле Блазиуса:
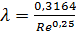 ;
;
- если ReI < Re < ReII, то режим движения турбулентный, зона смешанного трения, и λ определяем по формуле Альтшуля:
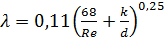 ;
;
- если Re > ReII, то режим движения турбулентный, зона шероховатых труб, и λ определяем по формуле Шифринсона:
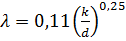 .
.
Результаты вычислений сводим в соответствующие для каждого трубопровода таблицы. Для расчета следует брать 5…7 значений расхода.
Таблица 1 – Гидравлический расчет i-го трубопровода
| № | Расход, Q, м3/ч | Расход, Q, м3/с | Скорость, v, м/с | Re, Зона трения | λ | Σh |
| … |
Далее решаем полученную выше систему уравнений, либо аналитически, либо графоаналитически, в зависимости от условий задачи.
Если в какой-либо из труб известен расход, то уравнение для данной трубы решается аналитически. Далее идет графоаналитическое решение. Рассмотрим графоаналитическое решение для заданной схемы трубопроводов в общем случае.
Графический способ основан на построении графиков функций левой и правой частей уравнений системы и нахождении соответствующих точек их пересечения.
Построим график уравнений (2), (3), (4), (5) в координатах Н-Q.
По оси ординат отложим величину статического напора 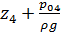 , и добавим к ней гидравлическую характеристику трубопровода 4. Построенная кривая является графическим изображением уравнения (4) Нк(Q4). Далее, на оси ординат отложим величину статического напора в трубопроводе 3, и от нее построим гидравлическую характеристику трубопровода 3. Получим графическое изображение уравнения (3), т.е. Нк(Q3).
, и добавим к ней гидравлическую характеристику трубопровода 4. Построенная кривая является графическим изображением уравнения (4) Нк(Q4). Далее, на оси ординат отложим величину статического напора в трубопроводе 3, и от нее построим гидравлическую характеристику трубопровода 3. Получим графическое изображение уравнения (3), т.е. Нк(Q3).
Далее, на основании уравнения (5), сложим графически кривые (4) и (3) путем добавления расхода в трубопроводе 3 к расходу в трубопроводе 4 при одинаковом значении напора (показано отрезками). Полученная пунктирная кривая представляет собой эквивалентную гидравлическую характеристику трубопроводов 3 и 4, т.е. Нк(Q3 + Q4).
Откладываем по оси ординат величину гидродинамического напора на выходе из насоса 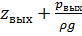 и из него вычитаем рассчитанную ранее гидравлическую характеристику трубопровода 2. Получаем графическое построение уравнения (2), т.е. Нк(Q). Точка А пересечения кривых (2) и (5) дает графическое решение относительно напора в узле К и расхода Q.
и из него вычитаем рассчитанную ранее гидравлическую характеристику трубопровода 2. Получаем графическое построение уравнения (2), т.е. Нк(Q). Точка А пересечения кривых (2) и (5) дает графическое решение относительно напора в узле К и расхода Q.
Так как кривая (5) получена путем сложения расходов в трубопроводах 3 и 4, то, проводя горизонтальную прямую от точки А до пересечения с кривыми (3) и (4), получим значения расходов Q3 и Q4.
Таким образом, при постановке вопроса об определении расхода в трубах, задача решена.
Если, при заданной схеме трубопроводов, надо определить диаметры трубопроводов 3 и 4, то при этом будет задано значение общего расхода в сети и давление на выходе из насоса рвых. В этом случае составляется уравнение Бернулли для трубопровода 2:
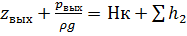 ,
,
из которого аналитически определяем величину напора в узле К, т.е. Нк. Далее, как было показано выше, записываем уравнения Бернулли для труб 3 и 4 (уравнения (3) и (4)). В соответствии с этими уравнениями решаем задачу третьего типа на расчет простого трубопровода (определение диаметра).
Тогда, задаваясь значениями диаметров (5…7 значений), рассчитываем потери напора в трубопроводах 3 и 4, и представляем их в табличном виде:
| № п/п | d | Re | λ | Σhi |
| … |
Далее строим график зависимости по уравнениям, полученным из (3) и (4):
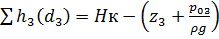 ,
,
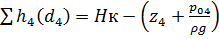 .
.
На оси ординат откладываем величину 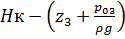 и
и 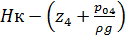 , и проводя горизонталь до пересечения с построенной кривой Σhi(di), получаем соответствующее значение диаметра.
, и проводя горизонталь до пересечения с построенной кривой Σhi(di), получаем соответствующее значение диаметра.
Все расчеты могут быть выполнены в прикладных компьютерных программах, например, Excel и др., или вручную. При этом значение одной параметрической точки (Qi или di) должно быть представлено в виде полного расчета.
На основании проведенного графоаналитического расчета должны быть сделаны выводы об искомых значениях расходов, диаметров, давлений и т.д. Если, при проведении расчетов, выясняется, что исходные данные противоречат реальным гидравлическим условиям течения жидкости (т.е. заданный напор слишком велик, диаметры либо слишком малы или велики, скорости течения жидкости резко отличаются от величин 1…5 м/с) следует обратиться к ведущему преподавателю для изменения исходных условий.
Рекомендуемая литература:
1. Сборник задач по машиностроительной гидравлике: Учеб. пособие для машиностроительных вузов / Д.А. Бутаев, З.А. Калмыкова, Л.Г. Подвизда и др.; Под ред. И.И. Куколевского, Л.Г. Подвизда. – 5-е изд., стереотипное. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. – 448с., ил.
2. Гидромеханика: учеб. пособие по решению задач / Л. Н. Раинкина - М.: Нефть и газ РГУ нефти и газа им. И.М. Губкина, 2005. - 131 с.
3. Гидравлика, гидромашины и гидроприводы: учеб. для втузов / Т. М. Башта, Б. Б. Некрасов, С. С. Руднев. - 2-е изд., перераб. - М.: Машиностроение, 1982. - 423 с.: ил.
Дата добавления: 2015-04-18; просмотров: 364; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Список использованных источников. 1. Гидравлика и гидравлические машины / Э | | | Основные определения |