Слов’янський державний педагогічний університет

Міністерство освіти та науки України

Слов’янський державний педагогічний університет

Технологічний факультет

Кафедра машинознавства і основ виробництва

Програма

і методичні рекомендації до вивчення курсу

“Гідравліка”

для студентів спеціальності 7.01.01.03.

“Педагогіка середньої освіти. Трудове навчання”

Слов’янськ, 2004 р.

Програма і методичні рекомендації до вивчення курсу “Гідравліка” для студентів спеціальності 7.01.01.02. “Педагогіка середньої освіти. Трудове навчання” складено відповідно до навчального плану підготовки спеціалістів.

Програма і методичні рекомендації затверджено на засіданні кафедри машинознавства і основ виробництва “___”_________ 2004р.

Затверджено вченою радою Слов’янського державного педагогічного університету від “___”___________ 2004 р.

Рекомендовано для студентів вищих навчальних закладів спеціальності 7.01.01.03 “ПМСО. Трудове навчання”.

Укладачі: доц. Лазаренко О. Я.

ст.. викл. Лазаренко Т.В.

Рецензенти: доц. Перепічаєнко Є.К.

доц. Шумілова Е.Д..

Слов’янський державний педагогічний університет

ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ

В основу методических указания положена программа Министерства просвещения СССР по курсу "Гидравлика к гидравлические машины" для специальности № 2120 "Общетехнические дисциплины и труд" педагогических ин­ститутов.

Курс "Гидравлика и гидравлические машины" состоит из следующих частей:

· гидравлики - основной теоретической части, при изучении которой студенты знакомятся с законами равновесия и движения несжимаемой жидкости;

· гидравлических машин, при изучении которых студенты знако­мятся с устройством, принципами действия, областью примене­ния различных гидравлических машин-преобразователей и гид­равлических двигателей.

Для изучения курса рекомендуются следующие учебники:

1. Башта Т.М., Руднев С.С., Некрасов Б.Б. и др. Гидравлика, гидравлические машины и приводы", М.,1970 г.

2. Угинчус А.А. "Гидравлика и гидравлические машины", Харьков,1970.

3. "Лабораторный курс гидравлики, насосов и гидропередач" под ред. Руднева С.С. Додвиза Л. Г., П., 1979.

4. Юшкин В.В. "Гидравлика и гидравлические машины", Минск,1974.

Для изучения курса достаточно иметь одну из первых двух книг. Библиотека института располагает учебником - Угинчус А.А. "Гидравлика и гидравлические машины" - в достаточном количестве.

Для лучшего усвоения учебного материала учебным планом предусматривается выполнение студентами лабораторных работ в лаборатории института икраткий курс лекций. Кроме того, предусматривается выполнение одной контрольной работы по изучае­мому курсу. Содержание контрольных заданий приводится далее.

Контрольную работу студент-заочник должен отправить инсти­туту не позже, чем за 10 дней до начала экзаменационной сессии. Контрольные задания, отправленные позже, проверяются лишь после экзаменационной сессии. Выполненные и оформленные лабораторные работы студент обязан защитить. Зачет по курсу "Гидравлика я гидравлические машины" выставляется после защиты всех лабора­торных работ иконтрольного задания.

Сроки сдачи зачетов определяются деканатом, однако во всех случаях зачет сдается очно.

Не останавливаясь, на общих требованиях четкости к аккуратности при выполнении контрольного задания ставится в извест­ность, что:

1. В контрольной работе обязательно пишется условие задачи.

2. Вычерчивается необходимая схема или рисунок.

3. Выписывается условие задачи только того варианта, который относится к исполнителю. (Согласно двум последним цифрам своего шифра. В случае несоответствия варианта контрольное задание не под­лежит рассмотрению).

4. Обязательно ставить размерности величин.

Ниже приводится программа по курсу "Гидравлика и гидравли­ческие машины", Просвещение, Москва, 1981 г.;

1. Введение (1 ч.)

Краткий обзор развития гидравлики и гидромашиностроения. Роль отечественных ученых в их эволюции. Значение гидромашино­строения, гидротехники в народном хозяйстве страны и перспектив вы развития в свете решений партии и правительства.

Связь курса гидравлики и гидравлических машин с технически­ми дисциплинами, программой трудового обучения в школе.

2. Основы гидростатики (8 ч.)

Жидкость. Физические свойства жидкости: плотность, сжимаемость, температурное расширение, вязкость, внутреннее трение в жидкости.

Силы, действующие на покоящуюся жидкость. Гидростатическое дав­ление и его свойства.

Дифференциальные уравнения равновесия жидкости. Основное урав­нение гидростатики. Закон Паскаля и его техническое применение. Закон Архимеда.

3. Основы гидродинамики (10 ч.)

Задачи гидродинамики. Основные определения. Уравнение неразрывнос­ти потока. Ламинарный и турбулентный режим движения. Число Рейнольдса и его критическое значение. Понятие о гидродинамическом подобии. Физический смысл числа Рейнольдса.

Напорное и безнапорное движение. Общие свойства равномерного движения. Ламинарное движение в круглой трубке. Поле скоростей. Формула Пуазейля.

Энергия элементарной струйки и потока жидкости. Уравнение Бернулли и его практическое применение. Потери по длине потока и местные потери.

Классификация трубопроводов. Расходные характеристики Гидравлический расчет простого водопровода.

Истечение жидкости через малое отверстие в тонкой стенке. Типы сжатия струи. Истечение жидкости через насадки. Типы на­садок и их гидравлические коэффициенты. Применение насадок в технике.

Явление гидравлического удара и его фазы. Н.Е. Жуковский -создатель теории гидравлического удара. Прямой и непрямой удары. Методы снижения ударного давления.

Классификация и принцип действия гидравлических машин.

4. Гидравлические машины (7 ч.)

Типы и принцип действия насосов. Основные параметры насо­сов - напор и производительность. Мощность и КПД насосов. Явление кавитации.

Объемные насосы: поршневые, пластинчатые, шестеренчатые,

вин­товые, диафрагменные. Устройство, характеристика, область примене­ния.

Лопастные насосы: центробежные и пропеллерные (осевые), устройство, характеристика, область применения.

Гидроэлеваторы (водоструйные насосы), принцип действия, об­ласть применения.

Гидравлический привод. Объемный гидропривод, общие понятия, достоинства, недостатки, область применения. Гидравлические передачи: типы передач, устройство, назначение, области применения. Краткая история гидропривода в Советском Союзе и перспектива развития.

5. Гидросиловые установки (4 ч.)

Гидроэнергетические, ресурсы (мировые и СССР). План ГОЭЛРО и роль гидростанций в электрификации СССР.

Классификация гидроэлектростанций: приплотинные, деривацион­ные, гидроаккумуляторные. Основные сооружение, оборудование, приму - щества производства электроэнергии на ГЭС. Приливные электро­станции.

Гидротурбины. Типы и принцип действия гидравлических турбин. Важнейшая характеристика, КПД и применение гидравлических турбин.

Важнейшие гидротехнические сооружения в СССР и за рубежом.

Перспективы гидроэнергетики.

Литература

Гидравлика, гидравлические машины и гидропривод. Под ред. Т.М.Вашты.М.,1970.

Лабораторный курс гидравлики, насосов и гидропередач. Под ред. С.С. Руднева, Л.Г. Подвиза. М., 1974.

Савин И.Ф., Сафонов П.В. Основы гидравлики и гидропривод. М., 1978.

Юшкин В.В Гидравлика и гидравлические машины. Минск, 1974.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

К ИЗУЧЕНИЮ КУРСА

Изучение курса "Гидравлика и гидравлические машины" рекомендуется начинать с определения его как научной дисциплины и установления его значения для преподавателя общетехнических дисциплин. При этом следует ознакомиться с историческим путем развития гидравлики, современным ее состоянием и перспективами развития. Следует особо отметить вклад русских и советских уче­ных и инженеров в разработку научных основ и инженерных вопро­сов гидравлики. Изучая историю развития гидравлики, следует уде­лить внимание задачам гидромашиностроения и гидроэнергетики в свете решений партии и правительства по развитию народного хо­зяйства СССР.

После этого можно перейти к изучению физических свойств жид­кости.

1. Жидкость и ее физические свойства.

Закон Ньютона для жидкости.

Жидкость - непрерывная среда, обладающая способностью изме­нять свою форму под действием малых сил.

Жидкое агрегатное состояние вещества - промежуточное между твердым и газообразным состоянием.

Наиболее характерным свойством жидкости является текучесть, т.е. легкоподвижность частиц.

При расчетах в гидравлике применяется техническая система единиц, а поэтому размерность:

массы кг∙сек²/м или кг (СИ)

плотность 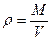кг∙сек²/м⁴ или кг/м³ (СИ)

удельный вес кг/м³ или н/м³ (СИ)

Сжимаемость, или свойство жидкости изменять свой объем под действием давления, характеризуется коэффициентом «ßρ» объёмного сжатия, который представляет собой относительное изменение объёма, приходящееся на единицу давления, т.е.

или см²/кг (1)

Температурное расширение жидкости - характеризуется коэффи­циентом «ß_T» объемного расширения, который представляет собой от­носительное изменение объема при изменении температуры на 1 °С, т.е.

(2)

Для воды коэффициент «ß_T» возрастает с увеличением давления и температуры.

Вязкость - представляет собой свойство жидкости сопротивлять­ся сдвигу (или скольжению) ее слоев. Вязкость есть свойство, про­тивоположное текучести: более вязкие жидкости (глицерин, смазоч­ные масла) являются менее текучими, и наоборот.

Вязкостью жидкостей обусловлена величина сил внутреннего тре­ния, возникающих в жидкости при перемещении слоев жидкости отно­сительно- других. Силы внутреннего трения, отнесенные к единице площади, дают величину касательных напряжений (τ).

Согласно гипотезе Ньютона, экспериментально обоснованной проф. Петровым, касательное напряжение внутреннего трения прямо пропор­ционально градиенту скорости в направлении, перпендикулярном дви­жению жидкости:

кг/м² или н/м²

Коэффициент пропорциональности «μ» зависит от свойств жидкости и называется динамическим коэффициентом вязкости жидкости:

μ [кг·сек/м²] или [н·сек/м²]

Отношение коэффициента динамической вязкости «μ» к плотности жидкости «ρ»называетеся коэффициентом кинематической вязкости:

м²/сек

При теоретическом изучении законов движения жидкостей важное значение имеет абстрактное понятие об идеальной жидкости, не обладающей вязкостью и не изменяющей своего объема под влиянием и температуры, т.е. имеющую постоянную плотность.

2. Основное уравнение гидростатики.

Эпюры гидростатического давления.

а) Силы, действующие в жидкости. Силы, действующие в жидкости, могут быть подразделены на силы поверхностные и силы массовые.

Поверхностные силы действуют на поверхностях, отделяющих рас­сматриваемый объем от окружающей среды. К этой категории сил от­носятся силы давления, являющиеся нормальными, силы внутреннего трения, являющиеся касательными. Массовые силы действуют на каждую частичку рассматриваемого объекта и пропорциональны, поэтому, его массе. К категории этих сил относятся сила тяжести и сила инерции.

б) Гидростатическое давление. Гидростатическим давлением в точке внутри жидкости называется сила, действующая на единицу площади по нормали к поверхности, если последняя стремится к нулю (т.е. при стягивании площадки в точку)

Так как касательные силы в покоящейся жидкости отсутствуют, то гидростатическое давление является результатом действия нормаль­ных сжимающих сил, т.е. поверхностных сил давления и массовых сил.

Гидростатическое давление в точке одинаково по всем направлениям (свойство жидкости) и зависит только от положения точки внутри жидкости и давления на свободной поверхности.

в) Гидростатическое давление покоящейся жидкости

,

где - давление на свободную поверхность;

h - глубина погружения донной точки;

- удельный вес жидкости.

Уравнение (4) называют основный уравнением гидростатики. Оно позволяет подсчитать давление в любой точке покоящейся жидкости. Это давление, как видно из урввнения, складывается из двух ве­личин: давления Р₀ на внешнюю (свободную) поверхность и давления, обусловленного весом вышележащих слоев жидкости ( h – избыточное давление).

Величина Р₀ является одинаковой для всех точек объема жид­кости, поэтому, на основании анализа уравнения, можно установить следующее: на сколько увеличивается давление на поверхность жидкости, на столько же увеличивается гидростатическое давление в рассматриваемой точке, или давление в жидкости передается во все стороны одинаково. Это положение носит название закона Паскаля о передаче давления внутри жидкости. На законе Паскаля основана работа широко распространенной гидравлической машины — гидравлического пресса.

Давление жидкости, как видно изформулы, растет с увеличением глубины по закону прямой и на данной глубине есть величина постоянная. Примеры эпюры давления на прямоугольную стенку приведены на рис. 1 "а" и "б"

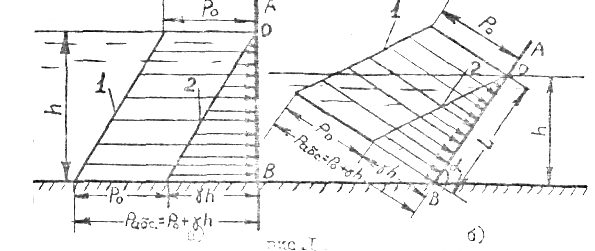
I - абсолютное давление; 2 — избыточное давление.

г) Для измерения давления применяются специальные приборы: пье­зометры жидкостные манометры, микроманометры, пружинные манометры и др.

Устройство и принцип работы их рассматривается на лабораторной работе по курсу «Гидравлика и гидравлические машины».

3. Уравнение непрерывности

(Уравнение расхода жидкости)

Основные параметры. Движение жидкости, при которой давление и ско­рость в любой точке пространства, заполненного жидкостью, с течением времени не изменяется, называется установившимся движением.

Путь, проходимый каждой точкой (частицей жидкости) при движении называют траекторией.

Линией тока называется такая кривая, в каждой точке которой в данный момент времени вектор скорости направлен по касательной. ( рис.2(а)). При установившемся движении линии тока совпадает с траекторией движения, частиц жидкости.

Если в поперечном сечении движущейся массы ходкости выцедить элементарную площадку ds и провести через все точки ее периметра линии тока, то совокупность линий тока образует так называемую трубку тока.

Количество жидкости, протекающее внутри такой: трубки тока по­стоянно, и образует так называемую элементарную струйку. (рис.2(б)).

Совокупность всех движущихся элементарных струек называется по­током жидкости.

Площадь поперечного сечения потока "S", нормального к направлению движения жидкости, называется живым сечением потока.

Уравнение непрерывности движения жидкости.

Расходом называется количество жидкости, протекающее через жи­вое сечение потока в единицу времени. Если рассматривать поток жидкости конечных размеров как совокупность бесконечно большого числа элементарных струек: с поперечным: сечением ds, то объемный расход потока Qбудет равен

(5)

где - истинная скорость, т.е. скорость в данной точке

Закон распределения скоростей по сечению потока зависит от ряда условий и часто представляет собой сложную функцию.

Вследствие этого практически оказалось удобным ввести поня­тие средней скорости потока (рис.3), являющейся фиктивной скоростью, при которой данное сечение пропускает тот же объемный расход, что и в действительности

Выражая объемный расход жидкости через среднюю скор ость, будем иметь

Q=V_cp·S (6)

рис. 3

Если в потоке несжимаемой жидкости произвольно выделить два поперечных сечения S₁ и S₂, причем средние скорости жидкости в этих сечениях будут соответствовать V_cp1 и V_cp2 (рис 4), то при установившемся движении все время будет иметь место соотношение

Q= V_cp1· S₁= V_cp2· S₂ = const (7)

Выражение (7), являющееся выражением материаль-ного баланса в установившемся потоке жидкости, называется уравнением постоянства расхода или уравнением непрерывности движения. Из него следует, что при установившемся движения несжимаемой жидкости расход ее в любом сечении потока постоянен.

(8)

Следовательно, средние скорости потока обратно пропорциональны площадям соответствующих живых сечений.

4. Уравнение Бернулли для потока вязкой жидкости

Графическое изображение.

Уравнение Бернулли устанавливает связь между давлением и скоростью в движущемся потоке жидкости и является основным уравне­нием гидравлики. Написанное для двух произвольных поперечных сечений элементарной струйки идеальной жидкости уравнение Бернулли имеет вид:

(9)

Координата "Z" [м], определяющая высоту положения частицы над какой-то плоскостью сравнения, называется геометрической высотой или геометрическим напором, и определяет запас потенциальной энергии, обусловленный положением частицы.

Величина (кг·м³/м²·кг) = [м], представляющая высоту столба жидкости,

уравновешивающего, действующее в данной точке давление, называется пьезометрической высотой или пьезометрическим напором, и определяет запас потенциальной энергии, обусловленный давлением.

Суммой этих двух величин называемой статической высотой, или статическим напором, определяется полный запас потенциальной энергии I кг жидкости относительно принятой плоскости сравнения.

Величина (м²·сек²/ сек²·м) = [м] представляет собой высоту столба жидкости, эквивалентную части статического напора, под действием которого происходит движение жидкости. Эта величина, называемая динамическим или скоростным напором, представляет собой удельную кинетическую энергия, т.е. кинетическую энергию, отнесен­ную к 1 кг жидкости.

Уравнение Бернулли показывает„что при установившемся движения идеальной жидкости сумма геометрического, пьезометрического и ди­намического напоров в каждом поперечном сечении элементарной струйки есть величина постоянная, т.е.

= const (10)

Физический (энергетический) смысл; этого уравнения заключается в том, что суммарная (полная) удельная энергия элементарной струйки идеальной жидкости при установившемся движении, состоящая из удельной потенциальной и удельной кинетической энергий, остает­ся посгоянной. Из уравнения Бернулли (10) и уравнения расхода (7) следует, что если площадь поперечного сечения струйки, уменьшается, т.е. струйка сужается, то скорость течения жидкости увеличивается, о давление уменьшается, и наоборот, если струйка расширяется, то скорость уменьшается, а давление возрастает.

Уравнение Бернулли для элементарной струйки вязкой (реальной) жидкости имеет вид:

+ H_пот (11)

где H_пот - дополнительный член в уравнении Бернулли, учитывающий потерю напора на участке между сечениями 1-1 и П-П.

При движении вязкой жидкости (реальной) часть энергии будет теряться на преодоление гидравлических сопротивлений и запас энергии Е во всяком последующем поперечном сечении струйки П-П будет меньше, чем в предыдущем 1-1, т.е.

E₁=E₂+ H_пот

Благодаря линейной размерности всех членов уравнения Бернулли, связь между напорами , чрезвычайно наглядно изображается графически

Линия А-А, характеризующая падение удель­ной энергии жидкости, называется линией энергии или напорной линией.

Отношение абсолютной величины потери напора H_пот к длине “l”, на которой она происходит, называется гидравлическим уклоном “i” т.е.

(12)

Линия Б-Б, характеризующая изменение; давления по длине струйки, называется пьезометрической линией.

Положение оси элементарной струйки В-В характеризует изменение геометрического напора вдоль трубки тока.

Плоскость 00, от которой производится отсчет геометрических высот, называется плоскостью сравнения.

Уравнение Бернулли для потока жидкости.

Чтобы практически использовать уравнение Бернулли, полученное для элементарной струйки, необходимо распространить его на целый поток, являющийся совокупностью элементарных струек, движущихся с различными скоростями.

При введении в уравнение Бернулли средней скорости потоке V_ср необходимо ввести в него поправочный коэффициент "α", т.к. кинетическая энергия потока, вычисленная по средней скорости, будет отличаться от истинной кинетической энергии потока.

Таким образом, уравнение Бернулли, написанное для установивше­гося потока реальной жидкости, имеет следующий вид:

(13)

Коэффициент Кориолиса "α" характеризует неравномерность распределения скоростей в поперечном сечении потока и представ­ляет собой отношение истинной энергии (кинетической) потока к кинетической энергии, вычисленной по средней скорости.

При равномерном движении воды в трубах и каналах небольшого поперечного сечения коэффициент "α" обычно близок к единице.

С помощью уравнения Бернулли решается большое количество за­дач, связанных с движением жидкости. На основании этого уравнения сконструирован ряд приборов и устройств, таких как водомер Вентури, водоструйный насос.

На рис.6 показан трубопровод диаметром “D”,на котором устроено сужение: диаметром "d"

В нормальной и суженной частях установлены два пьезометра (сечения 1, П). Пренебрегая величиной потерь напора между сечениями 1 и П, а также неравномерностью распределения скоростей по сечении (α=1), и принимая, что плоскость сравнения ОС проходит через ось трубопровода, можем записать уравнение Бернулли в таком виде:

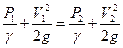(14)

Отсюда следует, что с увеличением скорости движения давление долж­но уменьшаться, и, наоборот, с уменьшением скорости давление должно увеличиваться. Это положение используется в водомере Вентури, где по разности показаний пьезометров “h” (см. рис. 6), зная диаметры "D"и “d”, можно определить расход.

В водоструйном насосе (рис.7) вода из бака "I" поступает в трубопровод, имеющий сужение. В узком сечении скорость струи воз­растает, и вода увлекает за собой воздух в коробке (смесительной камере), благодаря чему происходит подсасывание жидкости по трубке, опущенной в бак "2". При больших скоростях движение жидкости будет подсасываться из бака "2" непрерывно

По этому же принципу работают эжекторы и гидроэлеваторы.

5. Трубки полного и статического напоров

Труба Вентури

Если в каком-либо сечении потока жидкости (рис.8) установить две трубки - пьезометрическую "I" и скоростную (трубка Пито) "2", нижний изогнутый конец которой направлен против течения, то каждая из них покажет соответственно: статический напор и пол­ный .

Отсюда и их названия. В скоростной трубке создается дополнитель­ное давление от воздействия скорости движущейся жидкости. Высота подъема жидкости в скоростной трубке боль­ше высоты подъема жидкости в пьезометри­ческой трубке на величину скоростного напора . Для определения скорости движения жидкости необходимо измерить разницу между уровням жидкости в трубке полного гидродинамического напора "2" и пьезометре "I", т.е. высоту

Таким образом, скорость движения жидкости определяется по формуле:

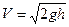(15)

Для удобства при измерении скорости потока с помощью скоростной трубки применяют совмещенную конструкцию (трубка в трубке) (рис .9).

Трубкой полного напора в этом случае является внутренняя трубка "А", воспринимающая полный гидродинамический напор .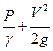

Об устройстве и назначении трубы Вентури см.§4, рис.6. 0тметим при этом, что в суженной части трубы Вентури возможно возникновение явления кавитации. Нарушение непрерывности потока жидкости, обусловленное появлением в ней пузырьков или полостей, заполненных паром или газом, называется кавитацией. Кавитация возникает при понижении давления, в результате чего жидкость закипает или из жидкости выделяется растворенный газ.

В потоке жидкости такое падение давления происходит обычно в области повышенных скоростей.

6. Режим движения вязкой жидкости, число Рейнольдса.

Потери напора при движении жидкости в трубе.

Предположение о существовании двух режимов движения жидкости было высказано великим русским ученым Д.И. Менделеевым еще в 1880г., В 1863 г. это предположение было подтверждено экспериментально английским ученым

0. Рейнольдсом. Рейнольдс пропускал воду через стеклянные трубки разного диаметра, регулируя скорость движения воды в них кранами "1" и "2" (рис.10) По тонкой трубке "3"с заостренным концом по входу в стеклянную трубку "4" подводилась окрашенная жид­кость из сосуда "5". Средняя скорость в трубке "4" площадью сечения "S"оп­ределялась по объему воды "V", посту­пившей в сосуд "6" за время "t" сек.

Опыты, проводившиеся при постоянном

напоре (для его поддержания была использована сливная труба "7"), показали, что при малых ско­ростях движения воды в трубке "4" краска движется в ней в виде тонкой струйки, не перемешиваясь с водой. После достижения опреде­ленной для данных условий опыта средней скорости движения воды, когда движение частиц жидкости приобретает как бы беспорядочный характер, струйка краски начинает размываться, отчего вся вода в трубке окрашивается.

Таким образом, поток жидкости в трубке может характеризоваться двумя режимами: I) ламинарным и 2) турбулентным (беспорядочным).

Опыты 0.Рейнольдса, а также исследования других ученых показа­ли, что основным критерием для определения режима движения жид­кости служит безразмерный параметр "R_е" (число Рейнольдса):

(16)

где - кинематический коэффициент вязкости.

Число Рейнольдса, при котором ламинарный режим переходит в турбулентный, называют критическим. По исследованиям Рейнольдса R_{е кр} = 2320. При R_е < 2320 движение жидкости происходит при ламинарном режиме, при R_е < 2320 движение жидкости происходит при турбулентном режиме. Скорость, соответствующую критическому числу Рейнольдса называют критической скоростью:

(17)

Решение многих практических задач гидравлики сводится к уста­новлению зависимости, определяющей изменения скорости и давления по длине потока. Для этого могут быть использованы:

уравнение постоянства расхода

Q=υ·s=const

и уравнение Бернулли

Эти уравнения обычно имеют три неизвестных: V, P, H_пот , поэтому для их решения необходимо третье уравнение. В качестве третьего уравнения используют зависимость потерь напора от скорости "V" и ряда другие факторов Потери напора (энергии) вызываются сопротивлениями двух видов:

1. Сопротивлениями по длине, обусловленными силами трения;

2. Местными сопротивлениями, обусловленными изменениями скорости

потока по величине кнаправлению.

Потери напора по длине трубопровода обычно определяют по фор­муле Дарси-Вейсбаха

(18)

а местные потери - по формуле Вейсбаха

(19)

где - коэффициент гидравлического трения;

l - длина трубопровода;

d - диаметр трубопровода;

V - средняя скорость потока;

S - коэффициент местного сопротивления.

Коэффициенты " " и "S" безразмерны. Экспериментальные иссле­дования показали, что эти коэффициенты зависят от многих факторов, в частности, от режима движения и шероховатости стенок.

Например, при ламинарном движении коэффициент трения " " определяется по формуле:

(20)

7. Водопроводы, их классификация и гидравлический расчет.

Явление гидравлического удара.

Трубопровод, по которому вода подается потребителю, называется водопроводом.

Водопровод, у которого диаметр трубы постоянен по всей длине и который не имеет боковых ответвлений, называется простым, водо­проводом; (рис 2, а). На простом водопроводе обычно имеется известное количество фасонных частей, создающих местные сопротивления

Водопровод, имеющей разветвления, а также со­ставленный из труб разных диаметров, называется сложным (рис. 2, б).

Различают короткие водопроводы, в кото­рых потери напора на местные сопротивления относительно велики и соизмеримы с потерями капора по длине (всасывающие трубы центробежных насосов), и длинные водопроводы, в которых потери напора на местные сопротивления составляют незначительную часть от потерь по длине (не более 5-10%).

Рассчитать водопровод - значит, определить, одну из трех вели­чин - расход "Q", потери напора "H_w" или диаметр трубы "d" по двум другим заданным. При гидравлическом расчете исходными со­отношениями являются уравнение Бернулли (9) и? уравнение постоян­ства расхода (7).

При движении воды по простому водопроводу потерю напора опре­деляют по формуле Дарси (18)

Учитывая, что в напорном потоке, когда труба работает полным сечением d=4R (где R - гидравлический радиус), можно переписать таким образом

(21)

Из этой формулы можно определить среднюю скорость потока

(22)

Гидравлическим радиусом "R" называет отношение площади живого сечения потока "S" к смоченному периметру, "f", т.е. R=S/f

Смоченным периметром называют длину контура живого сечения, которой жидкость соприкасается с твердыми стенками.

В формулу (22) введем обозначения:

гидравлический уклон

- скоростной множитель

Тогда получим так называемую формулу Шези

(23)

Умножив обе части уравнения (23) на площадь поперечного сечения трубы, получим выражение для расхода жидкости в трубе

Q=S·V=S·С (24)

Для упрощения расчётов произведение S·С обозначают через "K", тогда определения расхода воды получают формулу

(25)

где l – длина водопровода.

Величина "К" называется расходной характеристикой сечения. Она измеряется в тех же единицах, что и расход (м³ /сек).

Значения "К" приводятся в гидравлических справочниках в зависимости от диаметра и шероховатости трубы.

Для определения напора, теряемого по длине трубы, уравнение (25) решают относительно Н_w:

(26)

Для определения диаметра трубы уравнение (25) решают относи­тельно "К"

(27)

Вычислив "K²" , по таблицам получаем диаметр трубы.

Уравнения (25), (26), (27) применимы для решения водопроводов, работающих при турбулентном режиме в так называемой области квадратического сопротивления, когда V > 1,2 м/сек.

В правильно рассчитанных водопроводах могут возникать гидравлические удары. Явление резкого изменения давления в напорном трубопроводе, возникающее при быстром изменении скорости потока, назы­вается гидравлическим ударом.

Такое изменение давления в трубопроводе иногда превышает в де­сятки раз (и даже в сотни раз) обычное давление в нем, что оказы­вается опасным для прочности трубы и даже может вызвать ее разрыв.

Гидравлический удар возникает при внезапном закрытии задвижки на напорном трубопроводе и сопровождается резким увеличением дав­ления (кинетическая энергия движущейся массы жидкости преобразуется в энергию давления - потенциальную).

Согласно теории гидравлического удара, разработанной русским ученым, Н.Е. Жуковским, повышение давления, возникающее в жидкости при мгновенном закрытии задвижки, может быть определено по формуле

∆p= ·c·V (28)

где - плотность жидкости;

с - скорость распространения ударной волны в трубе;

V - скорость движения жидкости в трубе до закрытия задвижки.

Для ослабления гидравлического удара на водопроводных трубах устанавливается медленно закрывающиеся задвижки, воздушные кол­паки и предохранительные клапаны, автоматически открывающиеся при повышении давления выше нормального

8. Истечение жидкости через малые отверстия ив насадки

Малым отверстием будем считать такое, вертикальный размер ко­торого мал по сравнению с напором.

Чтобы исключить влияние толщины стенки и считать ее тонкой, кромки отверстия заостряются. (В технике часто приходится встре­чаться с истечением жидкости через различные отверстия)

Рассмотрим случай истечения жидкости в атмосферу при постоян­ном напоре через малое отверстие, в тонкой стенке. На рис. 1.2 показан в разрезе резервуар, в боковой стенке которого имеется отверстие диаметром "d" истечения из малых отверстий является наличие сжатого сечения расположенного на расстоянии 0,5 d от стенки. От­ношение площади сжатого сечения площади отверстия "S" называется коэффициентом сжатия струи

Для круглых отверстий =0,64 .Проведем плоскость сравнения 0-0 через центр тяжести отверстия и напишем урав­нение Бернулли для сечений 1-1 (свободная поверхность, жидкости в резервуаре) и П-П (сжатое сечение)

При постоянном напоре V₁=0; P₁=P₂=P_атм; Z₁=H; Z₂=0

Потеря напора определяется местным сопротивлением отверстия, т.е.

где - коэффициент потерь, равный 0,06.

Таким образом, уравнение Бернулли примет вид:

Отсюда скорость истечения , где - коэффициент скорости, равный, в среднем, 0,97.

Зная величину средней скорости истечения в сжатом сечении струи и величину площади сжатого сечения струи S_сж определим величину расхода

жидкости:

Q= S_сж·V₂

или, подставив значения S_сж, V₂:

(29)

где - коэффициент расхода;

S – площадь отверстия в тонкой стенке, м²

Среднее значение = 0,64 · 0,97 = 0,62

Насадком нааываедся короткий патрубок, присоединлемый к отверстию в гонкой стенке. Длина насадка обычно составляет (3 4)d, где d - диаметр выходного отверстия в стенке. Насадки применяют, главным образом, для увеличения пропускной способности отверстия.

В технике применяются следующие типы насадки (рис.1З):

а) цилиндрические - внешние;

б) цилиндрические внутренние;

в) конические сходящиеся;

г) конические расходящиеся;

д) коноидальнные.

Расход Q при истечении через насадки определяется по формуле (29): , где S - площадь, сечения выходного отверстия насадка; μ -коэффициент расхода, величина которого зависит от вида насадка или его конфигурации (рис. 13)

Увеличение расхода жидкости при истечении через цилиндрическийнасадок по сравнению с отверстием объясняется возникающими при входе в насадок сжатием струна затем постепенным ее расширением, с заполнением всего сечения насадка. Вследствие сжатия струи в насадке возникает вакуум. В результате этого происходит подсасы­вание жидкости и тем самым увеличивается пропускная способность насадка.

Внешний цилиндрический наездок имеет следующие истечения, отнесенные к расчетному выходному сечению:

ξ =1,0; φ=0,82; μ=φ=0,82.

Так как для круглого отверстия в тонкой стенке μ=0,62, то очевидно, что внешний цилиндрический наседок увеличивает расход в среднем в

раза

Конически сходящееся насадки широко применяют в технике, (в пожар­ных брандспойтах, в соплах гидромониторов и т. д.) для увеличения кинетической энергии струи.

Наибольшую пропускную способность при всех прочих равных условиях имеют коноидальные насадки (μ = 0,95 0,97).

9. Центробежные и осевые насосы.

Устройство и принцип работы.

Основным рабочим элементом цент­робежного насоса (рис.14) является рабочее колесо "I", расположен­ное на валу внутри корпуса "З", с изогнутыми лопастями "2". Корпус на­соса соединен со всасывающим "4" и нагнетательным "5" трубопроводами. Перед пуском насоса корпус его и всасывающий трубопровод заполняют жидкостью. При вращении рабочего ко­леса жидкость, находящаяся между ло­пастями, под действием центробежной силы отбрасывается к периферии, выходит в спиральную камеру и далее в нагнетательный трубопровод. В центральной части насоса, перед входом в рабочее колесо возникает разряжение, и вода под действием атмосферного давления направляется из источника по всасывающему тру­бопроводу в насос.

Центробежные насосы классифицируют по ряду признаков.

По напору различают насосы низконапорные: (до 20 м), средненапор­ные (от 20 до 60м) и высоконапорные (более 60 м).

По числу колес насосы делят на одноколесные и многоколесные. Многоколесными, как правило, делают высоконапорные насосы.

Для нормальной работы центробежных насосов вакуум в их всасывающем патрубке не должен превышать определенной величины - до­пустимой вакуумметрической высоты всасывания. Допустимая вакуумметрическая высота всасывания указывается в каталогах насосов и обычно не превышает 6-7 м.

При проектировании насосных установок различают геометрическую высоту всасывания Н_г.в. и вакуумметрическую высоту всасывания Н_вак Геометрическая высота всасывания - это разность отметок центра колеса и уровня воды в источнике. Вакуумметрическая высота всасывания складывается из геометрической высоты всасывания потерь напора во всасывающем трубопроводе h_nbи скоростного напора при входе в насос

Вакуумметрическая высота всасывания во избежание кавитации не должна превышать допустимой вакуумметрической высоты всасывания, т.е.

(30)

Полный напор H, который должен создавать центробежный насос, складывается из следующих величин (рис.15):

геометрической высоты всасывания Н_г.в.

геометрический высоты нагнетания Н_г.н.

потерь напора во всасывающем трубопроводе (с арматурой)

потерь напора в напорном трубопроводе (с арматурой) h_nн