Коэффициент продуктивности скважины.

формула радиального при­тока жидкости к скважине ; Из формулы видно, что дебит жидкости q зависит от депрессии , которая является независимым аргументом. Группу постоянных величин, входящих в эти фор­мулы, можно обозначить K. Таким образом, ; тогда дебит будет равен 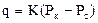- где q — дебит скважины при стандартных условиях, т/сут; K — коэффициент продуктивности, т/(сут-Па). Формула получила название формулы притока. Из нее видно, что приток линейно зависит от депрессии или при постоянном давлении на контуре от давления на забое сква­жины. Тогда 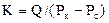; Графическое изображение зависимости 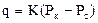называется индикаторной линией. Видно, что индикаторная линия должна быть наклон­ной прямой с угловым коэффициентом К. Чтобы построить ин­дикаторную линию, необходимо иметь несколько фактических значений дебитов и соответствующие этим дебитам забойные давления. Искривле­ние индикаторной линии в сторону оси давления означает увеличение фильтрационного сопротивления по сравнению со случаем фильтрации, описы­ваемым линейным законом Дарси. Искривление в сторону оси дебитов объясняется неодновре­менным вступлением в работу отдельных прослоев или пропластков и разными значениями в них пластовых давлений. Зная К, можно определить гидропроводность ε = kh/μ. Для этого надо решить формулу относительно kh/μ. Зная по геофизическим данным или по результатам глубинной дебитометрии h, а по лабораторным данным μ, можно опреде­лить проницаемость k в районе данной скважины. Обычно вме­сто R_к берут половину среднего или средневзвешенного по углу расстояния до соседних скважин. Для одиночно работающих скважин R_к принимают равным 250—400 м, исходя из физиче­ских представлений о процессах фильтрации.