Исходные данные задачи №1.02

Бригада	Производительность бригад, шт/ч	Фонд рабочего времени, ч
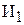
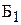
			9,5
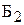
Заказ, шт

Ограничения по заказу изделий имеют следующую содержательную форму записи

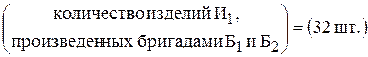
и

.

Математическая форма записи имеет вид

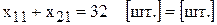и

.

Ограничение по фондам времени имеет содержательную форму

и

.

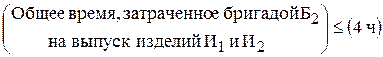Проблема заключается в том, что в условии задачи прямо не задано время, которое тратят бригады на выпуск одного изделия 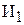или , т.е. не задана трудоемкость производства. Но имеется информация о производительности каждой бригады, т.е. о количестве производимых изделий в 1 ч. Трудоемкость Тр и производительность Пр являются обратными величинами, т.е.

.

Поэтому используя табл.1.2, получаем следующую информацию:

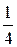® ч тратит бригада 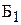на производство одного изделия ;

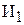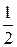® ч тратит бригада 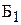на производство одного изделия ;

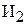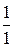® ч тратит бригада 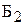на производство одного изделия ;

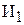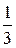® ч тратит бригада 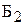на производство одного изделия .

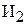Запишем ограничения по фондам времени в математическом виде

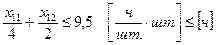
и

.

Неотрицательность объемов производства задается как

.

Таким образом, математическая модель этой задачи имеет вид

,

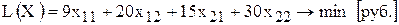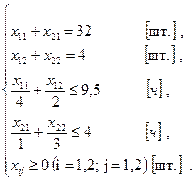
Задача №1.03*

Для пошива одного изделия требуется выкроить из ткани 6 деталей. На швейной фабрике были разработаны два варианта раскроя ткани. В табл.1.3 приведены характеристики вариантов раскроя 10 ткани и комплектность, т.е. количество деталей определенного вида, которые необходимы для пошива одного изделия. Ежемесячный запас ткани для пошива изделий данного типа составляет 405 . В ближайший месяц планируется сшить 90 изделий.

Постройте математическую модель задачи, позволяющую в ближайший месяц выполнить план по пошиву с минимальным количеством отходов.

Таблица 1.3

Характеристики вариантов раскроя отрезов ткани по 10

Вариант раскроя	Количество деталей, шт./отрез	Отходы, /отрез
1	2	3	4	5	6
							0,5
							0,35
Комплектность, шт./изделие