Средняя скорость жидкости в трубе круглого сечения с гидравлическим радиусом, равным 1 м, при расходе 5 м3/с, равна ____ м/с.

			0,4
			0,2
			0,5

Пример: Гидравлический радиус определяется по формуле: 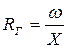(м)

R_Г – гидравлический радиус;

ω – площадь живого сечения потока (м²);

Х – смоченный периметр.

Для круглой трубы R_г = d/4. Определим диаметр трубы d = 4R_г = 1 х 4 = 4 м.

Рассчитаем площадь трубы ω = πd²/4, она равняется 12,56 м²/с.

Определим скорость движения жидкости 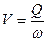, подставив данные получим V = 0,4 м/с.

8. Укажите на рисунке между сечениями 1–1 и 3–3 напорную линию.

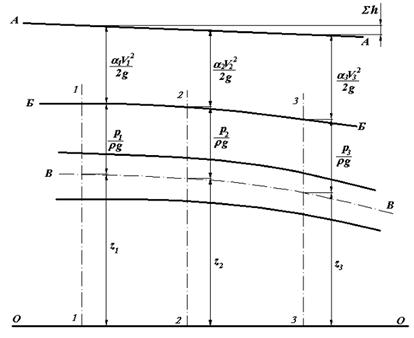
			А–А
			Б–Б
			В–В
			О–О

9. Коэффициент местных потерь на входе потока в трубу из бассейна или бака, равен …

			0,5
			1,0
			2,0
			5,0

Коэффициент гидравлического трения для потока жидкости при расходе жидкости равном 40 см³/с, диаметре трубы 0,03 м и коэффициентом вязкости 10^–6 м²/с составляет …

			0,038
			0,38
			0,076
			0,76

Пример: Выбор формулы для расчета коэффициента гидравлического трения λ производится в зависимости от величины числа Рейнольдса .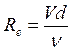

Рассчитаем скорость движения жидкости 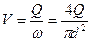. Переведя величину расхода в м³/с = 40·10^-6 м³/с. Определив скорость, подставим данные в формулу числа Рейнольдса и определим его величину R_е= 1699 т.е. меньше критического 2320, т.е. режим ламинарный. Для ламинарного режима λ вычисляется 64/R_е, подставив, получим 0,038.