Разрешение коллизий с помощью цепочек и открытой адресации

Подбор хеш-функции, обеспечивающей взаимную однозначность преобразования значения ключа в индекс элемента массива, в общем случае весьма трудная задача. На практике её можно решить только для постоянных таблиц с заранее известным набором значений ключа. Такие таблицы широко используются в трансляторах.

Поскольку взаимную однозначность преобразования значения ключа в индекс элемента массива в общем случае обеспечить практически невозможно (при соизмеримых значениях n и m), от требования взаимной однозначности отказываются. Это приводит к тому, что для некоторых различных значений ключа значение хеш-функции может быть одно и то же, т.е. H(ki)=H(kj). Это означает, что два элемента таблицы должны быть размещены в одном элементе массива, что невозможно. Такую ситуацию называют коллизией. Для разрешения коллизий используют различные методы. Наиболее часто используют для этого алгоритмы из двух основных групп, а именно: открытая адресация (методы двойного хеширования и линейного опробования) и метод цепочек.

В методе открытой адресации в качестве дополнительной СД используется массив, элементы которого могут содержать элементы таблицы. Каждый элемент массива имеет признак: содержит ли элемент массива элемент таблицы, содержал ли элемент массива элемент таблицы или элемент массива свободен. Для разрешения коллизий используется две хеш-функции: H1(k) и H2(a). Для выполнения операций поиска, включения, исключения, чтения и изменения элемента таблицы с ключём kj в этом случае применяется следующий алгоритм:

1.Вычислить ai=H1(kj).

2.Если при включении в таблицу новой записи элемент массива ai или содержал ранее элемент таблицы, но в настоящее время не содержит, а при исключении содержит элемент таблицы с ключём kj, то поиск завершён. В противном случае перейти к следующему пункту.

3.Вычислить ai= H2(ai) и перейти к пункту 2.

При включении новых элементов таблицы алгоритм остаётся конечным до тех пор, пока есть хотя бы один свободный элемент массива. При исключении элемента из таблицы алгоритм конечен, если таблица содержит элемент с заданным ключом. При невыполнении этих условий произойдёт зацикливание, против которого нужно принимать специальные меры. Например, можно ввести счётчик числа просмотренных позиций, если это число станет больше n, то закончить алгоритм.

Время выполнения операций над хеш-таблицей зависит от числа коллизий и времени вычисления значения хеш-функции, уменьшить которое можно путём использования “хорошей” хеш-функции. В случае целочисленного ключа в качестве хеш-функции часто применяется функция H1(k)=(C1*k+C2) mod n, где C1 и C2 - константы, взаимно простые числа. Если ключ нецелочисленный, то одним из простых методов получения хеш-функции является выделение части цифрового кода ключа. Например, пусть m£256, тогда H1(k) в качестве значения может иметь целочисленное представление первого или последнего байта ключа или какие-либо восемь разрядов из середины ключа. Для улучшения равномерности распределения значений хеш-функции применяют складывание кода ключа: первая половина кода складывается со второй и из результата выбираются какие-либо восемь разрядов. Можно также разделить код ключа на байты, а затем сложить их по модулю 28.

В качестве функции H2(a), называемой функцией рехеширования, может быть использована H2(a)=(a+C) mod n, где C - целочислен-ная константа. Если C=1, то метод разрешения коллизий называется методом линейного опробования, иначе – методом двойного хеширования. Недостатком метода линейного опробования является эффект первичного скучивания, который заключается в том, что при возникновении коллизии заполняются соседние элементы массива, увеличивая число проб при выполнении операции поиска. Особенностью хеш-таблиц является то, что время поиска элемента с заданным ключём не зависит от количества элементов в таблице, а зависит только от заполненности массива.

В методе цепочек элемент массива T с индексом ai содержит цепочку элементов таблицы, ключи которых отображаются хеш-функцией в значение ai. Для хранения таких цепочек элементов может быть использована дополнительная СД – линейный список (ПЛС или ОЛС), т.о. элемент массива T представляет собой линейный список. Алгоритмы включения и исключения элементов в такую таблицу очень просты.

Алгоритм включения/исключения элемента с ключём kj в таблицу:

1. Вычислить ai=H(kj).

2. Включить/исключить элемент в линейный список T[ai].

Для ускорения поиска элементов таблицы, ключи которых отображаются хеш-функцией в одно и тоже значение ai, в качестве элемента массива может быть использована СД типа БД.

25. Структуры данных бинарное дерево. Операции включения, исключения. Алгоритмы поиска и прохождения.

Бинарное дерево – конечное множество элементов, которое может быть пустым, состоящее из корня и двух непересекающихся бинарных деревьев, причем поддеревья упорядочены: левое поддерево и правое поддерево.

Между деревьями общего вида (узел дерева может иметь более двух сыновей) и бинарными деревьями существует взаимно однозначное соответствие, поэтому бинарные деревья часто используют для представления деревьев общего вида. Для такого представления используют следующий алгоритм:

1. изображаем корень дерева;

2. по вертикали изображаем старшего сына этого корня;

3. по горизонтали вправо от этого узла представляем всех его братьев;

4. пп. 1, 2, 3 повторяем для всех его узлов.

		Таким образом, получаем, что вертикальные ребра изображают левые поддеревья, а горизонтальные – правые. Данный алгоритм можно распространить и для леса.

Теорема. Число бинарных деревьев с n вершинами можно выразить формулой: 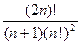. Например, для n=3 имеем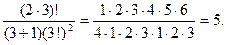

Проиллюстрируем этот пример графически: