Методы анализа рисков инвестиционного проекта

В мировой практике финансового менеджмента используются следующие методы анализа рисков инвестиционных проектов:

1) метод корректировки нормы дисконта;

2) метод достоверных эквивалентов (коэффициентов достоверности);

3) анализ чувствительности критериев эффективности (NPV, IRR и др.);

4) метод сценариев;

5) анализ вероятностных распределений потоков платежей;

6) деревья решений;

7) метод Монте-Карло (моделирование).

В общем случае можно выделить две составляющие риска инвестиционного 1) его стоимости (NPV) к изменениям значений ключевых 2) величину диапазона возможных изменений показателей, определяющую их вероятностные распределения. Поэтому все перечисленные методы количественного анализа инвестиционных рисков базируются на концепции временной стоимости денег и вероятностных подходах.

Метод корректировки нормы дисконта с учетом риска

Основная идея данного метода заключается в корректировке некоторой базовой нормы дисконта, которая считается безрисковой или минимально приемлемой (например, ставка доходности по государственным ценным бумагам, предельная или средняя стоимость капитала для фирмы), Корректировка осуществляется путем прибавления величины требуемой премии за риск, после чего производится расчет критериев эффективности инвестиционного проекта - NPV, IRR PI - по вновь полученной таким образом норме. Решение принимается согласно правилу выбранного критерия,

В общем случае, чем больше риск, ассоциируемый с проектом, тем выше должна быть величина премии, которая может определяться по внутрифирменным процедурам, экспертным путем или по формальным методикам. (Например, в качестве ориентира для установления премии за риск может приниматься коэффициент вариации. Чем больше этот коэффициент, тем большей должна быть величина премии за риск).

Метод достоверных эквивалентов (коэффициентов достоверности)

В данном методе, в отличие от предыдущего, осуществляется корректировка не нормы дисконта, а ожидаемых значений потока платежей CFt путем введения специальных понижающих коэффициентов аt для каждого периода реализации проекта. Теоретически значения коэффициентов at могут быть определены из соотношения

,

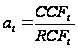где CCFt – величина чистых поступлений от безрисковой операции в периоде t (например, периодический платеж по долгосрочной государственной облигации, ежегодная сумма процентов по банковскому депозиту и др.); RCFt – ожидаемая (запланированная) величина чистых поступлений от реализации проекта в периоде t; t- номер периода.

Тогда достоверный эквивалент ожидаемого платежа может быть определен как

CCFt=at*RCFt, at≤1

Таким образом осуществляется приведение ожидаемых (запланированных)к величинам платежей, получение которых практически не вызывает сомнений и значения которых могут быть определены абсолютно точно (достоверно).

Однако в реальной практике для определения значений коэффициентов чаще всего прибегают к методу экспертных оценок. В этом случае коэффициенты отражают степень уверенности специалистов-экспертов в том, что поступление ожидаемого платежа осуществится (т.е. в достоверности его величины).

После того, как значения коэффициентов тем или иным путем определены, рассчитывают критерий NPV (IRR, РI) для откорректированного потока платежей по формуле

.

Предпочтение отдается проекту., скорректированный поток платежей которого обеспечивает получение большей величины NPV. Используемые при этом множители at получили название коэффициентов достоверности, или определенности.

Анализ чувствительности критериев эффективности

В общем случае этот метод сводится к исследованию зависимости некоторого результирующего показателя от вариации значений показателя, участвующих в его определении, Другими словами, этот метод позволяет получить ответы на вопросы типа: что будет с результирующей величиной, исходной величины? Отсюда его второе название - анализ «что будет, если».

Как правило, проведение подобного анализа предполагает выполнение следующих шагов:

задают взаимосвязь между исходными и результирующими показателями в виде математического уравнения или неравенства;

определяют наиболее вероятные значения для исходных показателей и возможные диапазоны их изменений;

путем изменения значений исходных показателей исследуют их влияние на конечный результат.

Обычная процедура анализа чувствительности предполагает изменение одного исходного показателя, в то время как значения остальных считаются постоянными величинами.

В EXCEL для моделирования подобных задач реализовано специальное средство - Таблица подстановки. Применение таблиц подстановки позволяет быстро рассчитать, просмотреть и сравнить влияние на результат любого количества вариаций одного показателя. В EXCEL два типа

с одним входом – для анализа влияния одного показателя;

с двумя входами - для анализа влияния двух показателей одновременно.

Метод сценариев

В отличие от трех предыдущих метод сценариев позволяет совместить исследование чувствительности результирующего показателя с анализом вероятностных оценок его отклонений. В общем случае процедура использования данного метода в процессе анализа инвестиционных рисков включает выполнение следующих шагов:

определяют несколько вариантов изменений ключевых исходных показателей (например, пессимистический, наиболее вероятный и оптимистический);

каждому варианту изменений приписывают его вероятностную оценку;

для каждого варианта рассчитывают вероятное значение критерия NPV (IRR, PI), а также оценки его отклонений от среднего значения;

проводят анализ вероятностных распределений полученных результатов.

Проект с наименьшим стандартным отклонением (у) и коэффициентом вариации (CV) считается менее рисковым.

В EXCEL реализовано специальное средство, которое позволяет создавать и сохранять в виде сценариев наборы входных значений, используемых для анализа различных ситуаций. Сценарий в EXCEL - это множество изменяемых ячеек, которое сохраняется под именем, указанным пользователем. Каждому такому набору соответствует своя модель предположений. Это позволяет проследить, как значения изменяемых ячеек влияют на модель в целом. Для каждого сценария можно определить до 32 изменяемых ячеек. Как правило, в качестве изменяемых ячеек используются те ячейки, от значений которых зависят ключевые формулы.

Для формирования сценария необходимо выбрать в главном тему Сервис пункт Сценарии. В появившемся диалоговом окне Диспетчер сценариев задаем операцию Добавить. Результатом выполнения указанных действий будет появление диалогового окна Добавление сценария. Вводим имя сценария, например Вероятный. При этом в поле Изменяемые ячейки автоматически будет поставлен выделенный пользователем блок ячеек (или вводим в это поле координаты входного блока), Поле Примечание заполняется по усмотрению пользователя. После нажатия ОК появится диалоговое окно Значения ячеек сценария, содержащее данные выделенного ранее блока. Завершив формирование сценария после нажатия Отчет (Итоги), указываем операцию Структура (Итоги сценария), и EXCEL сформирует отчет на отдельном листе рабочей книги под именем Структура сценария.

Анализ вероятностных распределений потоков платежей

Зная распределения вероятностей для каждого элемента потока платежей, можно определить ожидаемую величину чистых поступлений наличности M(CFt) в соответствующем периоде, рассчитать по ним чистую современную стоимость проекта NPV и оценить ее возможные отклонения. Проект с наименьшей вариацией доходов считается менее рисковым.

Проблема, однако, заключается в том, что количественная оценка вариации напрямую зависит от степени корреляции между отдельными элементами потока платежей. Рассмотрим два противоположных случая:

элементы потока платежей не зависят друг от друга во времени

(т.е. корреляция между ними отсутствует);

значение потока платежей в периоде t сильно зависит от значения потока платежей в предыдущем периоде (t-1) (т.е. между элементами потока платежей существует тесная корреляционная
связь).

Независимые потоки платежей

В случае отсутствия корреляции между элементами потока платежей ожидаемая величина NPV и ее стандартное отклонение у могут быть определены из следующих соотношений:

; ;

; ,

где M(CFt) - ожидаемое значение потока платежей в периоде i; CFit - i-и вариант значения потока платежей в периоде t; m - количество предполагаемых значений потока платежей в периоде t; pit - вероятность i-го значения потока платежей в периоде t; уt - стандартное отклонение потока платежей от ожидаемого значения в периоде t.

Сильно зависимые (идеально коррелированные) потоки платежей

В случае существования тесной корреляционной связи между элементами потока платежей их распределения будут одинаковы. Например, если фактическое значение поступлений от проекта в периоде отклоняется от ожидаемого на п стандартных отклонений, то все остальные элементы потока платежей в последующих периодах будут также отклоняться от ожидаемого значения на эту же величину. Другими словами, между элементами потока платежей существует линейная зависимость. Такие потоки платежей называют идеально коррелированными. В этом случае формулы расчетов существенно упрощаются:

; ;

.

Деревья решений обычно используются для анализа рисков проектов, имеющих обозримое или разумное число вариантов развития. Они особенно полезны в ситуациях, когда решения, принимаемые в момент времени t =n, сильно зависят от решений, принятых ранее, и, в свою очередь, определяют сценарии дальнейшего развития событий.

Дерево решений имеет вид нагруженного графа, вершины его представляют собой ключевые состояния, в которых возникает необходимость выбора, а дуги (ветви дерева) - различные события (решения, последствия, операции), которые могут иметь место в ситуации, определяемой вершиной. Каждой дуге (ветви) дерева могут быть приписаны числовые(нагрузки), например, величина платежа и вероятность его осуществления.