
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Жидкость находится в равновесии, т.е. действующие силы равны нулю.

Рис. 7. Схема для основного уравнения гидростатики
Определим силу давления Ра в точке М. Ро – давление на свободную поверхность. Угол a - произвольный наклон плоскости АВ, проходящий через точку М.
Выделим произвольный объем CDFE в жидкость и из условия равновесия рассмотрим действующие на объем силы.
Сила давления на поверхность CD равна
 ,
,
где dw - элементарная площадка
Сила давления на поверхность EF
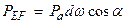
Вес жидкости в выделенном объеме жидкости

Из условия равновесия сумма проекции на ось Z

Сократив уравнение на общий множитель, получим уравнение
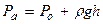
Вывод: давление на жидкость не зависит от угла наклона площадки, на которых оно действует.
4.2. Закон Паскаля. Гидравлический пресс
Из основного уравнения гидростатики следует, что давление в любой точке жидкости равно суммарному давлению, состоящему из давления, приложенного к свободной поверхности жидкости и веса жидкости.
Следовательно, давление, действующее на свободную поверхность, передается во все точки жидкости без изменения.
Паскаль установил, что жидкость (или газы) передают производимое на них давление во все стороны одинаково.
Различают следующие виды давлений:
- атмосферное (барометрическое)
- абсолютное
- избыточное (манометрическое)
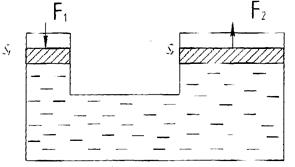
Рис. 8. Схема гидропресса
Принцип работы гидравлического пресса основан на законе Паскаля. Давление производимое на жидкость:
 ,
,
тогда по закону Паскаля
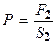
из соотношения  =
=  определяются искомые величины.
определяются искомые величины.
4.3. Уравнение неразрывности (сплошности) жидкости
Одной из задач гидродинамики является установление зависимости для основных показателей движения жидкостей. Внешние силы, действующие на жидкость предполагаются известным, искомым являются давление и скорость частиц жидкости. Плотность принимается постоянной.
Различают установившееся и неустановившееся движение жидкости. Установившееся – при котором скорость и давление в любой гидравлической точке не изменяются со временем. Неустановившееся – при котором скорость и давление изменяется с течением времени.
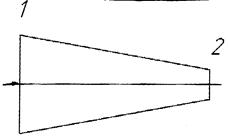
| |
Рис. 9. Участок трубопровода. (1 и 2 - живые сечения)
Рассмотрим установившийся поток жидкости между сечениями 1 и 2.
Объемный расход, проходящий через сечение 1

где u - средняя скорость потока
w - живое сечение
Так как втекаемый в сечение 1 объем жидкости равен вытекаемому из сечения 2, то имеет место равенство Q1 = Q2, тогда по аналогии

или
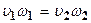
средние скорости потока обратно пропорциональны площадям соответствующих живых сечений.
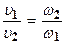 .
.
Примечание. Для газов используются массовые расходы, так как газ сжимаем.

следовательно М1 = М2 или


| |
Рис. 10. Уравнение Бернулли
Выберем в трубопроводе с движущейся жидкостью два произвольных сечения 1 и 2, в общем случае с разными живыми сечениями. Принимаем, что движение потока установилось. Под уровнением Бернулли понимается уравнение энергии движущейся жидкости. Тогда для сечения 1 имеем:
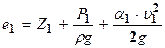 ,
,
где Z1 – удельная энергия положения
 - удельная энергия давления
- удельная энергия давления
 - удельная энергия скоростного напора
- удельная энергия скоростного напора
По аналогии, для сечения 2:

из – за потерь в магистрали е1 > l2 , следовательно
 ,
,
где a - коэффициент Кориолиса.
Так как скорости в сечениях 1 и 2 различны, то a учитывает неравномерность распределения скоростей в различных поперечных сечениях. Принято для ламинарного режима a »2, для турбулентного режима a » 1.
4.5. Уравнение Вентури
Уравнение устанавливает зависимость изменения скорости и давления движущейся жидкости в разных сечениях трубопроводов.
Рассмотрим участок трубопровода состоящего из двух колен, где диаметр D1, больше диаметра D2; живые сечения w1 больше w2. Применим уравнение неразрывности и уравнение Бернулли. Из u1w1 = u2w2 следует, что скорость u1 меньше u2.
 Рис. 11. Схема для вывода уравнения Вентури
Рис. 11. Схема для вывода уравнения Вентури
Уравнение Бернулли

В данном случае потери, коэффициент Кориолиса не учитываем сократив левую и правую часть на Z, т.к. Z1 = Z2, получим
 ,
,
откуда
 <
<  >
> 
То есть, при уменьшении площади живого сечения, давление Р уменьшается, а скорость u увеличивается.
4.6. Число Рейнольдса
Режимы течения жидкостей подразделяются на ламинарные – при котором жидкость движется слоями, не перемешиваясь, и турбулентное, при котором частицы жидкости перемешиваются.
Число Рейнольдса (Re) является критерием (показателем) режима течения жидкости.
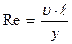 ,
,
где u - средняя скорость потока жидкости;
I – линейный (характерный) размер;
Y – кинематическая вязкость.
Следовательно, Rе – это безразмерная величина, отношение произведения средней скорости жидкости и линейного (характерного) размера к кинематической вязкости.
При напорном движении в круглых трубах за характерный размер l принимается внутренний диаметр D, в остальных случаях – гидравлический радиус

экспериментально установлено, что ламинарный режим устойчив при условии  < 2300
< 2300
Переход от ламинарного режима к турбулентному зависит кроме скорости, вязкости и размеров живого сечения, от возмущения источника питания гидросистемы, шероховатости стенок и др. Практически для турбулентного режима справедливо соотношение
 > 2300
> 2300
критическим числом Reкрит - является 2300 (граница раздела ламинарного и турбулентного режимов течения жидкости)

Рис. 12. Режимы течения жидкости
4.7. Уравнение энергии жидкости
Жидкостями называются тела, которые имеют определенный объем, но не имеют упругости формы, то есть, отсутствует модуль сдвига. Жидкости отличаются сильным межмолекулярным воздействием и, в следствие этого, малой сжимаемостью. Коэффициент сжимается для жидкостей изменяется в пределах от 2 · 10-6 до 2 · 10-4 отм-1. Для простых жидкостей, состоящих из симметричных сферических молекул, может быть получено уравнение состояния воды

где P – давление
u - средний объем одной частицы жидкости
k - постоянная Больцмана
Т – абсолютная температура
G (r) - радиальная функция распределения
u (r) – величина потенциала
d (r) – число частиц в шаровом слое (на расстоянии r)
4.8. Удельная энергия жидкости
В принципе понятие «энергия» – это способность тела совершать работу, обозначается символом Е.
Удельной называется энергия (е), приходящаяся на единицу силы тяжести.

где Е – общая энергия;
G – сила тяжести.
Удельная энергия е состоит из трех составляющих: 1 – энергия положения, 2 – энергия давления, 3 – кинетической энергии.
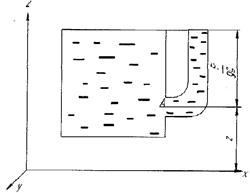 Рис. 13. Схема для расчета потенциальной удельной энергии
Рис. 13. Схема для расчета потенциальной удельной энергии
 Приведенный рисунок состоящий из емкости с жидкостью, выведенным пьезометром и системы координат, предназначен для определения удельной потенциальной энергии жидкости.
Приведенный рисунок состоящий из емкости с жидкостью, выведенным пьезометром и системы координат, предназначен для определения удельной потенциальной энергии жидкости.
Рис. 14. Схема для расчета кинетической
удельной энергии
1. 

Удельная энергия епол равна геометрической высоте точки жидкости над координатной плоскостью.
2 Удельная энергия давления. От уровня точки А выводится пьезометр


3. Удельная энергия скоростного напора жидкости - екин
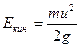


Следовательно, удельная энергия жидкости

5. ГИДРАВЛИКА ТРУБОПРОВОДОВ
Участок магистрали (трубопровода), соединяющий насос с резервуаром (баком), принято называть всасывающей магистралью (линией); участок трубопровода, по которому жидкость от насоса поступает в гидравлический двигатель, — напорный (рабочий или нагнетательный), и участок трубопровода, по которому жидкость отводится из нерабочей полости гидравлического двигателя в резервуар, называется сливной магистралью. К напорной магистрали относятся также все трубопроводы, находящиеся под рабочим давлением.
5.1. Расчет сечения трубопровода
Расход Q жидкости через данный трубопровод, площадь f его сечения и средняя по сечению скорость uтечения жидкости связаны соотношением

Сечения прочих каналов гидроагрегатов, по которым течет жидкость, рассчитываются на основе закона неразрывности потока (постоянства расхода), согласно которому расходы в различных сечениях потока при установившемся движении одинаковы:

или
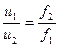
где и1 и и2  — средние скорости потока в сечениях f1 и f2 каналов.
— средние скорости потока в сечениях f1 и f2 каналов.
При выборе величины скорости потока (течения жидкости) в трубопроводе и каналах арматуры необходимо учитывать, что повышение скорости приводит к увеличению сопротивления (потерь) систем, а снижение — к увеличению веса трубопроводов и арматуры. Увеличение площади поперечно сечения каналов (трубопроводов) приводит к неблагоприятным конструкциям элементов гидропривода, а также повышает влияние сжимаемости жидкости, что ухудшает характеристики привода по показателям жесткости. Допустимая скорость течения жидкости является также функцией рабочего давления.
На основании практических данных можно рекомендовать для напорных трубопроводов следующие величины скоростей:
Давление в кГ/см2 ………..............10 25 50 100 150 200
Допустимая скорость жидкости
в см/сек ………………………..130 200 300 450 550 600
В гидросистемах станков при коротких трубопроводах (l/d < 100, где l и d – соответственно длина и диаметр сечения трубопровода) скорость жидкости обычно находится с следующих пределах (в м/сек):
Всасывающие трубопроводы……………………..0,5 – 1,5
Сливные трубопроводы открытых систем…………..2
Нагнетательные трубопроводы……………..……… 3-5
Для длинных трубопроводов (l/d > 100) эти данные уменьшают на 30 – 50%.
В общем случае скорость выбирают такой, чтобы потери напора в трубопроводе не превышали 5 – 6 % рабочего давления.
В авиационных гидросистемах скорости в напорной и сливной магистралях доводят до 30 м/сек.
Скорости (в м/сек) движения жидкости по рекомендации некоторых иностранных фирм следующие:
Магистраль:
всасывающая………………………………………….1,2
сливная…………………………………………………2
нагнетательная при давлении в кГ/см2:
25…………………………………………………...3
50…………………………………………………...4
100…………………………………………………...5
150……………………………………………….более 5
Скорости применяемые в общем машиностроении США, приведены ниже.
Элементы гидросистемы Скорость
в м/сек
Линия всасывания диаметром 12,7 – 25,4 мм………………..0,6-1,2
То же диаметром больше 32 мм…………………………………1,5
Линия нагнетания диаметром от 12,7 до 50,8 мм ……………...3,0
То же диаметром больше 50 мм…………………………………3,6
Клапаны управления и прочие короткие участки с зажатым
сечением………………………………………………………6,0
Переливные и предохранительные клапаны…………………...30,0
5.2. Режимы течения жидкости
Течение реальных (вязких) жидкостей по трубопроводам гидросистемы и каналам ее агрегатов сопровождается гидравлическими потерями.
Различают потери, обусловленные трением, в зависимости от длины трубопровода, его диаметра, скорости рабочей жидкости и ее вязкости, а также потери в местных сопротивлениях, обусловленные в основном деформацией и изменением скорости (ускорением) потока жидкости.
Различают два режима течения жидкости в трубопроводах: ламинарный и турбулентный, причем переход от ламинарного к турбулентному режиму наступает при определенных условиях, характеризуемых числом Рейнольдса - Rе. Для труб круглого сечения этот критерий имеет вид

где и — скорость потока жидкости;
d — внутренний диаметр трубопровода;
 — кинематический коэффициент вязкости жидкости.
— кинематический коэффициент вязкости жидкости.
Для труб (каналов) некруглого и кольцевого сечений

где  гидравлический радиус сечения потока, представляющий собой отношение площади F сечения потока к смачиваемому периметру
гидравлический радиус сечения потока, представляющий собой отношение площади F сечения потока к смачиваемому периметру  . Для кольцевого трубопровода (щели) значение r обычно вычисляется
. Для кольцевого трубопровода (щели) значение r обычно вычисляется
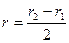
где r1 и r2 — внешний и внутренний радиусы щели.
Значения всех величин, входящих в приведенные выражения можно брать в любых согласованных размерностях.
Моменту перехода ламинарного режима в турбулентный и обратно соответствуют при данных условиях определенные критические значения Rе. Для ламинарного потока жидкости в гидравлически гладких металлических трубах круглого сечения это значение Rе ≤ 2200 ÷ 2300 и для турбулентного Rе ≥ 2200 ÷2300.
Для гидросистем, в которых расход жидкости зависит от потери напора, следует избегать чисел Рейнольдса Rе = 2200 ÷ 2500, ввиду неустойчивости в этом интервале течения и возможности появления в системе колебательных процессов.
5.3. Расчет потерь напора при движении жидкости
по длине трубопровода
5.3.1. Ламинарный режим течения
Потеря напора (давления) Δр в цилиндрическом прямом отрезке трубы, обусловленная сопротивлением трения жидкости при течении ее в ламинарном режиме (Re < 2300), вычисляется по известным выражениям, полученным из уравнения Пуазейля:


где μ и ν – соответственно коэффициент абсолютной и кинематической вязкости жидкости;
γ и ρ – объемный вес и плотность жидкости;
g – ускорение силы тяжести;
L и d – длина и диаметр внутреннего сечения рассматриваемого отрезка трубы;
р1 и р2 – давление в начале и в конце этого отрезка трубы;
Q и u – средние значения расхода и скорости жидкости в трубе.
В том случае, если искомой величиной является расход жидкости или диаметр сечения трубы, предпочтительнее пользоваться преобразованными выражениями
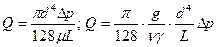 *
*
Для удобства вычислений последнее уравнение можно представить с учетом распространенных в практике единиц:


или

Для практических расчетов часто также пользуются приведенными ниже выражениями с неоднородной размерностью входящих в них величин:


и

где L и d – в см; Q – в см3/сек; ν – в ссm (мм2/сек);
р – в кГ/см2; γ – в г/см3.
Путем введения коэффициента  и соответствующих преобразований выражение (*) можно привести к виду
и соответствующих преобразований выражение (*) можно привести к виду

или

где Н и Δp – потеря напора (давления) соответственно в единицах столба (Н) жидкости и удельного давления Δp;
 λ – коэффициент сопротивления трения.
λ – коэффициент сопротивления трения.
Рис. 15. Зависимость коэффициента гидравлического
сопротивления λ от числа Рейнольдса и шероховатости трубы
Расчетное значение этого коэффициента для ламинарного течения (Re < 2300; рис. 6) равно

С учетом дополнительных сопротивлений, вызываемых, в основном, сужением и прочими искажениями сечения труб, а также охлаждением наружных слоев жидкости, соприкасающихся со стенками трубы, значение λ при практических расчетах труб следует принимать для ламинарного режима

Потери напора Н и давления Δp связаны для несжимаемой жидкости соотношением
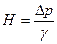
При расчетах гидравлических систем с низким давлением и особенно потоков жидкости со свободной поверхностью обычно пользуются выражением напора Н. В настоящем пособии рассматриваются, в основном, системы высокого давления, для которых сопротивления (потери напора) обычно не выражаются в виде разности уровней, ввиду чего будем пользоваться выражением для давления и применять при вычислении потерь напора (энергии) размерности удельного давления.
Приведенные выражения справедливы для отрезков труб такой длины, потери на входе которых являются по сравнению с потерями по их длине пренебрежимо малыми. К подобным отрезкам труб относится подавляющее большинство таких трубопроводов, которые в практике относят к «коротким».
Для очень коротких труб, потери на входе которых не являются по сравнению с потерями по длине пренебрежимо малыми, пользуются выражением

где ζвх – коэффициент сопротивления входа в трубу; для коротких отрезков круглых труб можно принимать ζвх = 0,5 ÷ 1,0.
5.3.2. Турбулентный режим течения
Потеря напора при турбулентном режиме течения жидкости рассчитывается по выражению, причем коэффициент сопротивления λ для гидравлической гладкой трубы вычисляется для условий 2300 < Rе < 8000 по полуэмпирической формуле Блазиуса 
Гидравлически гладкой трубой принято считать такую трубу, в которой выступы шероховатости скрыты в толще ламинарного граничного слоя жидкости у стенок.
Ввиду того, что с увеличением числа Рейнольдса толщина ламинарного пограничного слоя уменьшается, выступы шероховатостей трубы могут оголиться, в результате труба перестанет быть гидравлически гладкой. В соответствии с этим на величину коэффициента λ при турбулентном потоке может оказывать в этом случае влияние величины шероховатости поверхности стенок трубопровода.
Для значения Rе < 100 000 толщина этого пограничного слоя в трубе круглого сечения может быть определена по следующей эмпирической зависимости:

где d — внутренний диаметр трубы,
Принято считать трубу гладкой, относительная шероховатость внутренней поверхности которой, равная отношению средней высоты выступов (величина абсолютной шероховатости k к внутреннему диаметру трубы d, составляет
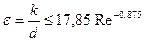
Ниже приведены величины Rе, при которых трубы перестают быть гидравлически гладкими:
ε …………...........0,01 0,005 0,002 0,001 0,0005
10-3 Re …………...5,2 11,5 32,75 72,3 160
Практически можно считать, что абсолютная шероховатость k цельнотянутых труб из меди, латуни, алюминия и свинца равна 0,01—0,015 мм, стальных цельнотянутых труб 0,04—0,08 мм новых чугунных труб 0,2—0,3 мм. Следовательно, цельнотянутые трубы из стали, латуни в меди можно принимать гидравлически гладкими на всем диапазоне чисел Рейнольдса, встречающихся в рассматриваемых гидросистемах.
При числах Рейнольдса ~ 80 тыс. и выше коэффициент сопротивления λ, становится независимым от числа Рейнольдса и является функцией лишь относительной шероховатости, в связи с чем потеря напора будет пропорциональной квадрату скорости потока жидкости. В частности для применяемых в гидравлических системах машин цельнотянутых стальных труб диаметром d > 6 мм коэффициент сопротивления при 2300, < Rе < 80 000 можно принять равным в среднем λ = 0,025.
При этом допущении формула для расчета гидравлических потерь в прямом отрезке такой трубы примет вид

Для стальных труб диаметром 4 мм расчетное значение
λ = 0,03; для труб диаметром 2 мм λ = 0,04.
При течении жидкости в изогнутых коленах (закруглениях труб) возникают дополнительные потери, обусловленные при ламинарном потоке нарушением параболического характера скоростного поля, и в общем случае – потери, обусловленные изменением направления (поворотом) движущейся жидкости. Однако при ламинарном потоке коэффициент сопротивления для трубы с углом изгиба α ≥ 900 и при отношении среднего радиуса R изогнутого участка трубы к внешнему диаметр D сечения трубы R/D ≥ 4 практически равен коэффициенту сопротивления в прямолинейной трубе. Для труб с изгибом, выполненным под углом α < 900, с отношением  < 4, коэффициент сопротивления составляет
< 4, коэффициент сопротивления составляет  .
.
5.4. Местные гидравлические потери
Местными гидравлическими потерями называется удельная энергия жидкости, идущая на преодоление сопротивлений при течении ее через гидроагрегаты и арматуру. Эти потери вызываются в основном деформацией потока и изменениями его скорости и направления течения, сопровождающимся закручиванием потока, образованием вихрей и пр.
Величины местных сопротивлений могут достигать больших значений. Так, например, потери напора а арматуре и изгибах трубопроводов могут в несколько раз быть выше, чем в прямых участках трубопровода; изгиб трубы под углом 900 с внутренним радиусом изгиба, равным диаметру трубы оказывает сопротивление, примерно равное сопротивлению прямой трубы длиной 40 диаметров.
Потери напора в местных сопротивлениях выражаются в долях скоростного напора и подсчитываются по выражениям

где  и Н – потери напора соответственно в единицах удельного давления и высота столба жидкости;
и Н – потери напора соответственно в единицах удельного давления и высота столба жидкости;
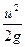 - удельная кинетическая энергия (скоростной напор) потока;
- удельная кинетическая энергия (скоростной напор) потока;
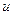 - средняя по сечению потока скорость жидкости;
- средняя по сечению потока скорость жидкости;
 - коэффициент местного сопротивления, учитывающий все потери напора, в том числе обусловленные трением, ускорениями, завихрениями и пр.
- коэффициент местного сопротивления, учитывающий все потери напора, в том числе обусловленные трением, ускорениями, завихрениями и пр.
Коэффициент  относится к условному проходу местного сопротивления (обычно к площади присоединительного канала) и показывает какая часть скоростного напора
относится к условному проходу местного сопротивления (обычно к площади присоединительного канала) и показывает какая часть скоростного напора 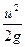 расходуется на преодоление данного местного сопротивления. Поскольку при движении жидкости через гидроагрегаты происходит интенсивная турбулизация потока, обусловленная чередующимися местными сопротивлениями связанными короткими каналами, значение критического числа Рейонльдса в большинстве случаев здесь не может быть примерно, ввиду чего им обычно пренебрегают, принимая приближенно величину его для данного местного сопротивления постоянной. Это позволяет считать потерю напора от местного сопротивления пропорциональной квадрату средней скорости жидкости на входе в рассматриваемое сопротивление.
расходуется на преодоление данного местного сопротивления. Поскольку при движении жидкости через гидроагрегаты происходит интенсивная турбулизация потока, обусловленная чередующимися местными сопротивлениями связанными короткими каналами, значение критического числа Рейонльдса в большинстве случаев здесь не может быть примерно, ввиду чего им обычно пренебрегают, принимая приближенно величину его для данного местного сопротивления постоянной. Это позволяет считать потерю напора от местного сопротивления пропорциональной квадрату средней скорости жидкости на входе в рассматриваемое сопротивление.
Средние значения коэффициента  для наиболее часто применяемых в гидросистемах местных сопротивлений приведены ниже:
для наиболее часто применяемых в гидросистемах местных сопротивлений приведены ниже:
| а) для распределительных золотников в зависимости от характера движения и количества поворотов потока жидкости ………………………………………………… | 2-4 |
| б) для распределительных и обратных (запорных) клапанов (без учета усилия пружины)…………………….. | 2-3 |
| в) для самозапирающихся соединений (муфт) ……….. | 1-1,5 |
| г) для штуцеров, присоединяющих трубы к агрегатам, и переходников, соединяющих отрезки труб …………. | 0,1-0,15 |
| д) для угольников с поворотом под прямым углом …... | 1,5-2 |
Коэффициенты плавных колен (отводов) трубопроводов под углом 900 с относительным радиусом изгиба  , где r - радиус изгиба и d – внутренний диаметр трубы приведены на рис. 16. и прямоугольных тройников с разделением потоков, а также угольников с поворотом под различными углами и проходных угольников – на рис. 17.
, где r - радиус изгиба и d – внутренний диаметр трубы приведены на рис. 16. и прямоугольных тройников с разделением потоков, а также угольников с поворотом под различными углами и проходных угольников – на рис. 17.
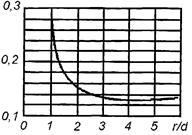
Рис. 16. Зависимость коэффициента местного сопротивления закругленной трубы под углом 900 от относительного радиуса изгиба r/d.

Рис. 17. Коэффициенты местных сопротивлений
5.4.1. Потери в золотниковых распределителях
Одним из наиболее распространенных видов местных сопротивлений являются золотниковые распределители. Данные исследований показывают, что вследствие возмущающего действия поворотов, а также сужений и расширений критическим числом для золотниковых распределителей является значение  , а следовательно, поток жидкости в распределителях является преимущественно турбулентными. В соответствии с этим можно считать, что гидравлические характеристики (потери напора Δр) распределителей весьма близки к параболе и могут быть определены зависимостью
, а следовательно, поток жидкости в распределителях является преимущественно турбулентными. В соответствии с этим можно считать, что гидравлические характеристики (потери напора Δр) распределителей весьма близки к параболе и могут быть определены зависимостью
 ,
,
где Q – расход жидкости;
s – площадь проходного сечения;
γ – объемный вес жидкости;
ζ – коэффициент сопротивления;
g – ускорение силы тяжести.
Значение ζ для золотниковых распределителей обычно колеблется в пределах ζ = 3 ÷ 5.
Потери напора в золотниковом распределителе зависят также от вязкости жидкости. Эта зависимость может быть достаточно точно выражена эмпирическим выражением
 ,
,
где ν – вязкость жидкости в сст;
и – скорость потока жидкости в м/сек;
g – ускорение силы тяжести в м/сек2.
Приведенные данные можно применять лишь для приближенных расчетов гидросистемы. Для точных расчетов требуются дополнительные данные испытания (проливки) конкретных местных сопротивлений в реальных условиях их работы.
5.4.2. Вход в трубу
Практический интерес представляет местное сопротивление, оказываемое при входе жидкости в трубу из большого объема, в качестве которого здесь служит жидкостный бак, силовой цилиндр, пневмогидравлический аккумулятор, фильтр и др. Под большим объемом понимается объем с площадью сечения в плоскости, перпендикулярной к оси отверстий (трубы) ≥ F ≈ 100 f, где f – площадь сечения отверстий. Расчет потерь для этого случая ведется по формуле, причем под и понимается средняя скорость жидкости в трубе.
Коэффициент ζ при острых кромках входного отверстия (рис. 18) можно принять равным 0,5. При входных кромках отверстия, закругленных по дуге круга, величина коэффициента ζ уменьшается, достигая при отношении r/D = 0,1 ÷ 0,2, где r – радиус закругления входной кромки и D – диаметр отверстия, значения 0,05 – 0,03. При заделке трубы в плоскую стенку коэффициент повышается до 0,5.
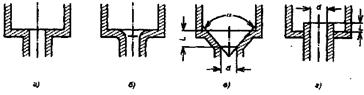 Рис. 18. Схема ввода жидкости в трубу
Рис. 18. Схема ввода жидкости в трубу
Уменьшить коэффициент сопротивления на входе жидкости из большого объема в трубу можно также выполнением на входе в нее фасок, причем значение коэффициента зависит от величины угла α конуса и относительной длины 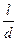 конуса, где l и d – параметры конуса. Для практического применения может быть рекомендован конус с относительной длиной
конуса, где l и d – параметры конуса. Для практического применения может быть рекомендован конус с относительной длиной  и с углом α =
и с углом α =  . Величина коэффициента сопротивления в этом случае составляет 0,1 – 0,15.
. Величина коэффициента сопротивления в этом случае составляет 0,1 – 0,15.
Если труба диаметром d заделана в резервуар так, что ее конец входит в резервуар находится на некотором расстоянии l от его стенки (дна), на величину коэффициента сопротивления будет, помимо прочего, влиять относительное расстояние 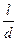 среза трубы от стенки; величина коэффициента для этого случая может быть принята равной ζ = 1.
среза трубы от стенки; величина коэффициента для этого случая может быть принята равной ζ = 1.
5.4.3. Внезапное сужение трубопровода
 В случае, если вход жидкости в трубу происходит из трубы большего сечения, имеют место условия течения жидкости с внезапным сужением трубопровода (рис. 19).
В случае, если вход жидкости в трубу происходит из трубы большего сечения, имеют место условия течения жидкости с внезапным сужением трубопровода (рис. 19).
Рис. 19. Расчетная схема внезапного сужения трубопровода
Величина потерь напора для этого случая с внезапным сужением может быть выражена общим уравнением
 ,
,
где и – скорость жидкости в трубе меньшего диаметра.
Коэффициент сопротивления ζ для этого случая зависит от отношения диаметров d2 и d1 труб малого и большого сечений (влиянием числа Re пренебрегаем).
Для практических расчетов можно пользоваться данными, проведенными ниже:
 ….. …..
| 3,5 | 2,5 | 2,0 | 1,5 | 1,25 | 1,1 | 1,0 | ||
| ζ…….. | 0,45 | 0,43 | 0,42 | 0,4 | 0,37 | 0,28 | 0,19 | 0,1 |
В общем случае коэффициент сопротивления при внезапном сужении трубопровода рассчитывается по выражению (в расчетах принимается скорость жидкости в трубе малого сечения)
 ,
,
где F и f – площадь сечений трубопровода соответственно до сужения и в месте сужения.
Для уменьшения вихреобразований и связанных с ним потерь напора, имеющих место при внезапных сужениях, переходную кромку закругляют или выполняют на ней фаску. Максимальный эффект достигается при постепенном (коническом) сужении с плавным сопряжением конического и цилиндрического участков. Для этого может быть рекомендован конус с углом α = 40 ÷ 600. Величина коэффициента ζ в этом случае может быть взята равной 0,1 – 0,15.
5.4.4. Внезапное расширение трубопровода
Условия, соответствующие внезапному расширению трубы, имеют место при вводе жидкости из трубы в баки, силовые цилиндры, пневмогидравлические аккумуляторы, фильтры и прочие емкости.
Величина потери напора для случая внезапного расширения трубы равна скоростному напору потерянной скорости (теорема Борда-Карно):

где  и
и  - скорости в трубах малого и большого сечений.
- скорости в трубах малого и большого сечений.
При истечении в трубу (резервуар и прочее) с большим поперечным сечением величина  практически равна нулю в соответствии с чем потеря напора составит
практически равна нулю в соответствии с чем потеря напора составит
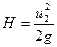 .
.
5.4.5. Сложение потерь
Общая потеря напора в магистрали равна сумме потерь в отдельных ее компонентах. Однако простое суммирование потерь допустимо лишь в том случае, если расстояние между местными сопротивлениями будет больше участка, необходимого для стабилизации потока после прохождения им каждого местного сопротивления. Так, например, жидкость, поступающая из трубы с турбулентным течением в трубу с ламинарным течением, должна протечь некоторый участок трубопровода, прежде чем установится профиль скоростей, соответствующий ламинарному течению. Этот участок называется входным (начальным). При нарушении ламинарного течения каким-либо местным сопротивлением течение стабилизируется также после прохождения жидкостью какого-то пути. Например, нарушение потока, возникающее в отводах, сохраняется на расстоянии около 50 диаметров трубы. Длина lст участка стабилизации может быть подсчитана по выражению

где d – внутренний диаметр трубы.
При тщательном закруглении входных кромок трубы длина начального участка, на котором заканчивается формирование ламинарного потока, уменьшается до ~ 0,029 Red.
Местные сопротивления стремятся по возможности разделить прямолинейными участками и расположить их друг от друга на расстоянии  . При необеспечении этого условия поток не успевает стабилизироваться и расчет потерь на местных сопротивлениях усложняется.
. При необеспечении этого условия поток не успевает стабилизироваться и расчет потерь на местных сопротивлениях усложняется.
Поскольку местные сопротивления магистралей гидравлических систем машин устанавливаются на произвольных расстояниях, потери в них можно учесть лишь приближенно. Трудно также учесть взаимное влияние друг на друга местных сопротивлений, обусловленное малыми расстояниями между ними. Поэтому при практических расчетах трубопроводов потерями на входе и взаимным влиянием местных сопротивлений ввиду их относительно небольшой величины в сравнении с общими потерями обычно пренебрегают.
6. КАВИТАЦИЯ ЖИДКОСТИ
Под кавитацией понимается местное выделение из жидкости в зонах пониженного давления ее паров и газов (вскипание жидкости) с последующим разрушением (конденсацией паровых и смыканием газовых) выделившихся парогазовых пузырьков при попадании их в зону повышенного давления. Это разрушение пузырьков сопровождается местными гидравлическими микроударами большой частоты и высокого уровня ударных давлений.
Кавитация нарушает нормальный режим работы гидросистемы, а в отдельных случаях может вызвать разрушение ее агрегатов. Разрушительному действию кавитации подвергаются насосы, золотники, клапаны и прочие гидроагрегаты, причем это действие проявляется зачастую в очень короткое время. Так, например, наблюдаются случаи выхода из строя аксиально-поршневых насосов, происходящие в результате кавитационного разрушения (износа) распределительной пары и сопровождающегося недопустимого падения производительности за время работы от 20 мин. до 1 ч.
Схематически механизм возникновения кавитации и его разрушительного действия сводится к следующему. При понижении давления жидкости в како – либо точке потока до некоторой величины жидкость вскипает (происходит ее разрыв), выделившиеся же пузырьки газа и пара увлекаются потоком и переносятся в область более высокого давления, в которой паровые пузырьки конденсируются, а газовые сжимаются (смыкаются). Так как процесс конденсации парового сжатия газового пузырька происходит мгновенно, частицы жидкости перемещаются к его центру с большой скоростью, в результате кинетическая энергия соударяющихся частиц вызывает в момент смыкания пузырьков местные гидравлические микроудары, сопровождающиеся высокими забросами давления и температуры в центрах пузырьков (по расчетам температуры могут достигать значений 1000 – 15000 С и выше в местное давление может достигать 1500 – 2000 кг/см2).
В том случае, если эти процессы протекают вблизи от стенок ограничивающих каналов, последние будут подвергаться непрерывным гидравлическим ударам (бомбардировкам), которые вызывают местные высокие температуры, развивающиеся в результате скачкообразности процесса и высокого уровня забросов давления. Указанные ударные действия частиц жидкости дополняются химическим воздействием на металл кислорода воздуха, выделяющегося из жидкости, а также воздействием электролитического характера.
 Под действием высоких температур в присутствии кислорода воздуха происходит активное окисление (коррозия) контактирующих поверхностей. Происходящие при этом окислительные процессы усугубляются тем, что растворенные в жидкости воздух содержит почти в полтора раза больше кислорода, чем атмосферный воздух. Кроме того, интенсивность окислительных процессов повышается в результате разрушения под действием гидравлических микроударов окислительной пленки, которая в обычных условиях замедляет окисление металлических поверхностей деталей.
Под действием высоких температур в присутствии кислорода воздуха происходит активное окисление (коррозия) контактирующих поверхностей. Происходящие при этом окислительные процессы усугубляются тем, что растворенные в жидкости воздух содержит почти в полтора раза больше кислорода, чем атмосферный воздух. Кроме того, интенсивность окислительных процессов повышается в результате разрушения под действием гидравлических микроударов окислительной пленки, которая в обычных условиях замедляет окисление металлических поверхностей деталей.
Рис. 20. Характер кавитационного разрушения плунжера
распределительного золотника следящей гидросистемы
В результате при длительной кавитации под действием указанных гидравлических ударов высокой повторяемости и одновременном воздействии высокой температуры происходит разрушение (эрозия) поверхностей деталей.
Кавитация наступает тем раньше, чем больше жидкость загрязнена твердыми частицами. Это обусловлено тем, что на поверхностях этих частиц адсорбируется тонкий слой воздуха, частицы которого при попадании в зону пониженного давления служат очагами, способствующими возникновению кавитации.
Разрушению подвергаются при развитой кавитации детали различных гидроагрегатов. На рис. 20 показан плунжер распределительного золотника (клапан) следящей гидросистемы, работавший в условиях значительного дросселирования жидкости. Кавитационному разрушению подвергаются также торцы блока цилиндров и межоконные перемычки распределительного диска аксиально-поршневых насосов, на поверхности которых образуются глубокие питинги и выколы.
При возникновении кавитации в трубопроводах сопротивление их значительно возрастает, а пропускная способность соответственно уменьшается. При небольших сечениях трубопровода, образуются газовые пробки и движение жидкостно-газовых фаз происходит чередующимися импульсами.
Кавитация жидкости в насосах наступает при условия, когда жидкость при всасывании отрывается по тем или иным причина от рабочего элемента насоса — поршня, лопасти, зубьев или прочих вытеснителей. Возможность отрыва зависит от вязкости жидкости и величины давления на входе в насос, а также от числа оборотов и конструктивных особенностей насосов. В частности кавитация возникает, если давление на входе во всасывающую камеру насоса окажется недостаточным для обеспечения неразрывности потока жидкости в процессе изменения скорости дальнейшего ее движения.
Предельно допустимым, с этой точки зрения, числом оборотов насоса является такое число, при котором абсолютное давление жидкости на входе в насос будет способно преодолеть без разрыва потока потери напора во всасывающей камере, обусловленные ее сопротивлением и силами инерции. В случае шестеренного и пластинчатого (лопастного) насосов к этим потерям добавляются потери, обусловленные центробежной силой, действующей на жидкость, вращающуюся вместе с ротором насоса.
6.1. Способы борьбы с кавитацией
Основным способом борьбы с кавитацией является максимальное снижение разрежения в зонах возможной кавитации, которое частично может быть достигнуто за счет повышения окружающего давления. В частности, в борьбе с кавитацией во всасывающей камере насосов основным является обеспечение на всасывании такого давления, которое способно было бы преодолеть без разрыва потока жидкости гидравлические потери во всасывающей магистрали и в самой камере всасывания, включая сопротивление, обусловленное инерцией жидкости.
Очевидно, что для того, чтобы жидкость развила в рабочей камере насоса (в цилиндре и пр.) необходимое ускорение, требуемое для предотвращения отрыва ее от всасывающего элемента (поршня и пр.), к ней необходимо приложить соответствующее давление. Сила Р инерции жидкости при этом определится так:

где m – масса рассматриваемого объекта движущейся жидкости;
j – максимальное ее ускорение.
Для преодоления этой силы на входе во всасывающую камеру насоса должно действовать давление  , где F – сечение потока.
, где F – сечение потока.
Повышение давления достигается наддувом бака гидросистемы газом (поддавливанием), а также установкой подкачивающих насосов, эжекторов и прочими средствами.
В общем случае условие бескавитационной работы насоса можно выразить уравнением

где Рб – давление в жидкостном баке, питающем насос;
h – разность между уровнем жидкости в баке и выходным штуцером насоса;
Σрn – сумма потерь напора во всасывающей магистрали;
Рi – потеря напора, обусловленная ускорением жидкости во всасывающих каналах насоса и подводящем трубопроводе;
uвх- скорость жидкости во входном окне (канале) насоса;
γ – объемный вес жидкости;
Рк – критическое давление, при котором наступает активное выделение из жидкости пузырьков воздуха; это давление зависит от вязкости жидкости и ее температуры, а также от степени насыщения жидкости воздухом.
Ввиду трудности вычисления величины инерционной потери-напора рi она обычно учитывается запасом ра, значение которого обычно принимается для распространенных насосов и режимов их работы равным 300—400 мм рт. ст.
С целью снижения потерь напора во всасывающем трубопроводе необходимо устанавливать насос как можно ближе к питающему баку и ниже уровня жидкости в нем, а также увеличивать сечение трубопровода и уменьшать количество местных гидравлических сопротивлений на пути течения жидкости от бака к насосу.
Для обеспечения бескавитационных условий работы насосов применяют также различные конструктивные усовершенствования. Одним из радикальных способов борьбы с кавитацией в насосах является повышение давления на входе в насос, достигаемое применением вспомогательных насосов для подкачки или искусственного наддува газом жидкостных резервуаров, а также применением прочих средств, одним из которых является использование энергии потока жидкости в сливной магистрали гидросистемы с помощью эжекторов (рис. 21).
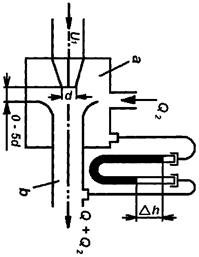 Рис. 21. Расчетная схема эжектора
Рис. 21. Расчетная схема эжектора
Расчет эжектора (при q = Q1/Q2 = 0 ÷ 1,5) обычно производят по эмпирической формуле (без учета потерь)
 ,
,
где q = Q2/Q1 – коэффициент смешения жидкостей (Q1 и Q2 – объемный расход эжектирующей и эжектируемой жидкости);
Δh – разность давлений в смесительной камере а и на выходе из диффузора b, в мм рт. ст.;

 - скоростной напор эжектируемого потока в мм. рт. ст.;
- скоростной напор эжектируемого потока в мм. рт. ст.;
u1 – скорость эжектируемого потока в м/сек;
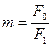 - коэффициент, характеризующий отношение площади F0 сечения смесительного трубопровода к площади F1 сечения сопла нам выходе.
- коэффициент, характеризующий отношение площади F0 сечения смесительного трубопровода к площади F1 сечения сопла нам выходе.
Длина смесительного трубопровода принимается равной (8 ÷ 10)d. При предварительных расчетах пользуются также упрощенной эмпирической формулой

Для уменьшения действия кавитации применяют коррозионно-стойкие материалы (стали с добавкой хрома и никеля) при одновременной тщательной обработке их поверхностей, омываемых кавитируемой жидкостью. Применяют также покрытия деталей материалом, стойким против кавитационного разрушения (бронзой, хромом и пр.).
Как правило, стойкость материалов кавитационному разрушению повышается с увеличением механической и химической (окислительной) стойкости, причем лучшие результаты дают материалы, в которых совмещаются оба эти качества. Наименьшую стойкость имеют чугун и углеродистая сталь и наибольшую стойкость — бронза и нержавеющая сталь. Наиболее стойким из известных материалов является титан.
Увеличение твердости материала повышает, как правило, антикавитационную стойкость. Так, например, увеличение твердости нержавеющей стали от НВ 150 до НВ 400—420 повышает ее антикавитационную стойкость в 10 раз и более. Увеличением твердости можно также несколько повысить антикавитационную стойкость углеродистых сталей, однако детали из этих сталей не могут обеспечить приемлемый ресурс времени при возможных твердостях.
Полностью устранить разрушительное действие кавитации путем применения стойких против коррозии материалов не представляется возможным. Разрушению, хотя и менее интенсивному, подвергаются при известных условиях детали из таких материалов как стекло, золото и пр., что свидетельствует о преобладании в рассматриваемом процессе их разрушения механических факторов.
6.2. Практическое использование эффекта кавитации.
 Эффект кавитации часто используют для практических целей. В частности он используется в устройствах для стабилизации расхода жидкости. Устройство (рис. 22а) состоит из дроссельной шайбы 1, измеряющей расход жидкости, и осесимметричной дроссельной иглы 2, служащей для введения устройства в кавитационный режим работы.
Эффект кавитации часто используют для практических целей. В частности он используется в устройствах для стабилизации расхода жидкости. Устройство (рис. 22а) состоит из дроссельной шайбы 1, измеряющей расход жидкости, и осесимметричной дроссельной иглы 2, служащей для введения устройства в кавитационный режим работы.
Рис. 22, а. Принципиальная схема кавитационного устройства для стабилизации расхода жидкости

Рис. 22, б. Кривая, характеризующая стабильность расхода
через кавитационное устройство.
При понижении давления Рвых на выходе, в данном случае из сопла Вентури, при постоянном давлении рвх на входе в него скорость потока жидкости будет повышаться, в соответствии с чем давление в суженном сечении сопла будет понижаться. После достижения этого давления до величины, соответствующей началу кавитации жидкости, последняя вскипает. Поскольку сопротивление сопла после этого будет увеличиваться пропорционально интенсивности кавитации, которая, в свою очередь, будет повышаться с увеличением перепада давления, расход через сопло после возникновения кавитации стабилизируется, сохраняясь постоянным независимо от дальнейшего снимания давления на выходе из сопла. При уменьшении этого давления будет лишь расширяться зона кавитации по диффузорной части, начиная от суженного сечения.
Подобные кавитационные устройства (сопла) используют для стабилизации расхода при колебаниях давления на выходе (при колебаниях нагрузки). Они обеспечивают регулирование расхода жидкости в большом диапазоне (≥ 10) при одновременной стабилизации расхода на каждом режиме.
На рис. 22, б показаны кривые зависимости регулируемого расхода Q жидкости от перепада давления на сопла при различных значениях (от 10 до 30 кГ/см2) давления рех на входе и давления Рвых выходе, изменяющегося от 0 до входного (30 кГ/см2). Измерения проведены при расходе жидкости от 500 до 40 000 см3/сек при давлениях Рвх = 10; 20; 25 и 30 кГ/см2.
Из графика следует, что расход жидкости сохранялся в постоянным (коэффициент расхода μ изменялся от 0,96 до 0,97) в широком диапазоне режимов. Нарушение стабилизированного расхода происходит практически при значениях критического давления на выходе Рвых ≈ Рвх, где Рвх – давление потока на входе в сопло.
Следует отметить, что заметного кавитационного разрушения поверхностей деталей при этом не происходит.
7. ГИДРАВЛИЧЕСКИЙ УДАР В ГИДРОУЗЛАХ
В связи с применением высоких скоростей течения жидкостей трубопроводах гидросистем современных машин (в ряде случаев эти скорости достигают 30 м/сек), а также в связи с распространением в них быстродействующих. распределительных устройств (скорости переключения доведены до тысячных долей секунды) важное значение приобретают вопросы, связанные с эффектом гидравлического удара, при котором забросы давления могут достигать четырехкратной величины рабочего давления в гидросистеме. Подобные забросы снижают ресурс работы трубопроводов и агрегатов, а в отдельных случаях могут вызвать их разрушение; в частности при гидроударах наблюдаются случаи разрушения охлаждающих радиаторов, корпусов фильтров и прочих гидроагрегатов. Кроме того, ударные забросы давления служат ложными сигналами, вызывающими нежелательные срабатывания датчиков и реле различных автоматических гидравлических приборов.
Гидравлическим ударом в общем случае называют забросы давления, сопровождающие всякий переходный процесс в жидкости от одного установившегося режима в жидкости к другому, обусловленный, к примеру, пуском и остановкой гидравлического механизма или иным изменением режима его работы. В частности, переходные процессы в гидросистемах с насосами постоянной производительности в основном обусловлены периодическими срабатываниями автомата разгрузки насоса, переключающими насосы на рабочий или холостой режим.
Аналогичное явление наблюдается и при переключении распределителей. Испытания показали, что при переключении распределителей с положительным перекрытием и клапанной разгрузкой насоса забросы при рабочих давлениях 100 кГ/смгдостигали значений 150 кГ/см2и выше (максимальное давление достигало 250 кГ/см2). Увеличение длины сливного трубопровода повышает заброс давления при срабатывании автомата разгрузки.
Из всего многообразия возможных форм, задающих возмущений, вызывающих гидравлический удар, нами будут рассмотрены лишь случаи возмущения, вызванные скачкообразным изменением скорости жидкости, при котором гидравлический удар достигает максимального значения.
Расчет величины ударного давления производят, пользуясь уравнением живых сил, согласно которому кинетическая энергия движущейся жидкости преобразуется в работу упругой деформации стенок трубы и сжатия жидкости. Для случая мгновенного полного перекрытия прямолинейного отрезка простого трубопровода, заполненного движущейся жидкостью, ударное повышение давления может быть вычислено по уравнению Н. Е. Жуковского
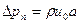
где ρ – плотность жидкости;
а – скорость ударной волны (скорость распространения импульса давления) в жидкости, заключенной в трубе;
u0 – начальная скорость движения в трубе (до начала перекрытия трубопровода).
Приведенное выражение будет справедливо, если перекрытие трубопровода произошло «мгновенно», т. е. для случая, когда время t перекрытия трубопровода меньше значения так называемого периода трубопровода (фазы удара) τ, под которым понимается время пробега ударной водной двойной длины рассматриваемого участка трубопровода (от задвижки до источника расхода и обратно):
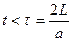
где L – длина участка трубопровода от источника расхода до задвижки.
При этом условии перекрытие трубопровода заканчивается до того, как обратная ударная волна, отраженная от источника расхода, вернется к задвижке. Гидравлический удар при этом определится полной потерей жидкостью скорости, в соответствии с чем повышение давления будет максимальным. Подобный гидравлический удар принято называть полным или прямым.
Из сказанного следует, что заброс давления при прямом гидравлическом ударе достигнет предельного значения лишь на том участке трубопровода, считая от задвижки (перекрывного крана), по которому успеет распространиться, прямая ударная волна, возникающая в момент полного закрытия задвижки, до встречи ее с обратной волной, отраженной от источника расхода.
Очевидно, что максимально возможное для возникновения прямого гидравлического удара значение времени перекрытия трубопровода (закрытия крана) равно  . Предельное ударное давление, равное по величине ударному давлению при мгновенном перекрытии трубы, будет наблюдаться при этом значении t лишь у самой задвижки. В остальных же сечениях по мере приближения к источнику расхода повышение давления снижается до значения давления в последнем.
. Предельное ударное давление, равное по величине ударному давлению при мгновенном перекрытии трубы, будет наблюдаться при этом значении t лишь у самой задвижки. В остальных же сечениях по мере приближения к источнику расхода повышение давления снижается до значения давления в последнем.
При условии  т. е. при более медленном, чем рассмотрено выше, перекрытии трубопровода, ударное повышение (заброс) давления определится лишь той частью начальной скорости жидкости
т. е. при более медленном, чем рассмотрено выше, перекрытии трубопровода, ударное повышение (заброс) давления определится лишь той частью начальной скорости жидкости  , которая будет потеряна (погашена) за время, равное периоду трубопровода τ. При этом условии обратная волна, отразившись от источника расхода, возвратится к задвижке (крану) раньше, чем трубопровод будет полностью перекрыт. Подобный удар принято называть непрямым или неполным.
, которая будет потеряна (погашена) за время, равное периоду трубопровода τ. При этом условии обратная волна, отразившись от источника расхода, возвратится к задвижке (крану) раньше, чем трубопровод будет полностью перекрыт. Подобный удар принято называть непрямым или неполным.
Ударное повышение давления в этом случае определится выражением

где  - уменьшение (потеря скорости жидкости в трубе), вызванное частичным перекрытием ее задвижкой, за время, равное периоду трубопровода τ;
- уменьшение (потеря скорости жидкости в трубе), вызванное частичным перекрытием ее задвижкой, за время, равное периоду трубопровода τ;
 - начальная скорость движения жидкости (скорость до начала перекрытия трубы);
- начальная скорость движения жидкости (скорость до начала перекрытия трубы);
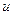 - измененная скорость жидкости (скорость к моменту прихода к задвижке обратной ударной волны, отраженной от источника, расхода).
- измененная скорость жидкости (скорость к моменту прихода к задвижке обратной ударной волны, отраженной от источника, расхода).
Допустив, что изменение скорости потока в трубе протекает равномерно, расчетное значение потери скорости  за время можно приближенно вычислить по выражению
за время можно приближенно вычислить по выражению

Заброс давления  при непрямом (неполном) ударе
при непрямом (неполном) ударе  может быть вычислен также по выражению
может быть вычислен также по выражению
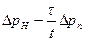
С учетом предыдущих уравнений последняя зависимость может быть представлена в виде
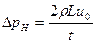
7.1. Скорость ударной волны
Входящая в приведенные выражения скорость а ударной волны (импульс давления) в упругой жидкости, заключенной в упругий трубопровод, определяется по уравнению
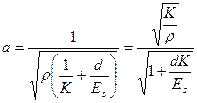
где  - плотность жидкости;
- плотность жидкости;
d и s – внутренний диаметр и толщина стенки трубы;
К – объемный модуль упругости жидкости; для деаэрированного минерального масла можно принять К = 1,6 · 104 кГ/см2;
Е – модуль упругости материала трубы; для труб из стали 1Х18Н9Т можно принимать Е = 2 · 106 кГ/см2.
Эта скорость для воды (плотность
Дата добавления: 2015-04-18; просмотров: 417; Мы поможем в написании вашей работы!; Нарушение авторских прав