Билет № 13

1. Механические колебания: основные характеристики гармонических колебаний; уравнение гармонических колебаний; свободные и вынужденные колебания; резонанс. Превращения энергии при гармонических колебаниях.

Колебание- движение, при котором тело (материальная точка) поочередно смещается то в одну, то в другую сторону. Условия, необходимые для наличия колебаний:

1)наличие возвращающей силы, возникшей в системе в результате выведения ее из положения равновесия;

2)отсутствие трения в системе (или очень мало);

3)система должна обладать инертностью.

Силу, под действием которой происходит колебательный процесс, называют возвращающей силой.

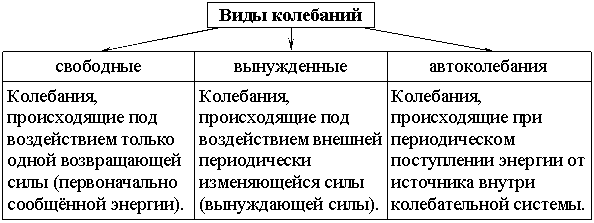
Колебания делятся также на периодические и непериодические

Простейшим видом периодических колебаний являются гармонические колебания, происходящие по закону синуса или косинуса.

Гармоническая колебательная система (система тел, совершающих колебания) обычно имеет одно положение, в котором может пребывать сколь угодно долго – положение равновесия О.

Отклонения от положения равновесия называют смещением, и обозначается Х, а наибольшее смещение (точки В или С) называется амплитудой колебания и обозначается А.

Периодические колебания совершаются циклично. Движение в течение одного цикла (когда тело, пройдя все промежуточные положения, возвращается в исходное) называется полным колебанием (О-С-О-В-О). Время одного полного колебания называется периодом колебания (обозначается Т).

Число колебаний в единицу времени называется частотой колебаний.

Число колебаний за 2π единиц времени называется циклической (круговой) частотой и обозначается ω:

График гармонических колебаний:

Математическая запись гармонических колебаний:

где – фаза колебания (физическая величина, определяющая положение колебательной системы в данный момент времени),

φ₀ – начальная фаза колебания.

При гармонических колебаниях скорость и ускорение тела также могут изменятся по закону синуса или косинуса.

Простейшими колебательными системами являются:

а) математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания под действием силы тяжести.

Период колебания определяется уравнением:

.

Период Т зависит лишь от длины маятника и местоположения (удалённости от центра Земли или другого небесного тела), которое определяется величиной ускорения свободного падения ;

б) пружинный маятник – материальная точка, закреплённая на абсолютно упругой пружине.

Период колебания определяется уравнением:

,

где m – масса материальной точки,

к – коэффициент упругости пружины.

Характерной особенностью колебательного движения является периодическое превращение кинетической энергии тела в потенциальную и обратно.

2. Принципы радиосвязи: амплитудная модуляция и детектирование. Развитие средств связи. Радиолокация. Радиосвязь на ж/д транспорте.

Ток высокой частоты создает в антенне электромагнитную волну, которая распространяется в пространстве. Электромагнитная волна, достигнув, приемную антенну

создает в ней ток такой же частоты, которую излучил передатчик.

Генератор незатухающих колебаний, изобретенный в 1913году, позволил осуществлять надежную и качественную радиотелефонную связь на большие расстояния.