Регулирование потоком возбуждения

Примем в уравнении ω=−(Rя+Rд)·M/(KΦ)^2 U=Uн=const,Rд=0,Φ=var, т.е. поток может уменьшаться от номинального. Тогда, переходя к относительным единицам, получим:

ν=1/f−μ/f2, (2.33)

где f=Φ/Φн – относительное значение потока.

При регулировании скорости примем μ=const. Тогда выражение (2.33) можно считать регулировочной характеристикой, которая является существенно нелинейной. Общий вид регулировочных характеристик представлен на рис. 2.7.а. Из рисунка видно, что характеристика имеет перегиб. Максимальное значение скорости соответствует точке перегиба, определим, как и ранее, известным поиском экстремума функции, т.е. из уравнения dν/df=0. В результате получим νm=1/(4μ) при значении регулирующего параметра fm=2μ.

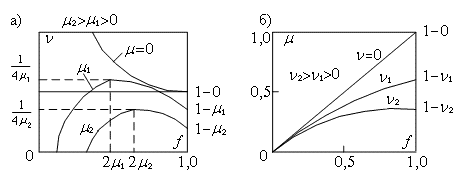Рис. 2.7. Регулировочные характеристики при изменении потока

Передаточный коэффициент для режима малых отклонений определяется по выражению

kν=dν/dff=f0=(f0−2(f0−μ))/f03, (2.34)

где f0 – значение управляющей координаты, относительно которой рассматриваются отклонения.

Обычно работают справа от точки перегиба, при уменьшении потока увеличивается скорость двигателя. Тогда диапазон регулирования скорости равен ν [(1−μ),1/(4μ)] при изменении регулирующего параметра в диапазоне f [1,2μ].

Для описания характеристики регулирования момента в (2.33) примем ν=const и перепишем уравнение в виде

μ=f·(1−νf). (2.35)

Регулировочная характеристика имеет вид (рис. 2.7.б). Координаты точки перегиба определим тем же способом. Они равны μm=1/(4ν), fm=1/(2ν). Регулирование момента можно осуществлять в диапазоне μ [0,1/(4ν)] при изменении регулирующего параметра в диапазоне f [0,1/(2ν)]. Передаточный коэффициент регулирования в режиме малых отклонений

kμ=1−2νf0. (2.36)

Для оценки энергетических показателей регулирования найдем, как связаны относительные скорости ν и ϖ в данном случае. Эту связь просто найти из соотношения

ν=ωω0/(ω0ω0н)=ϖ×Uн/(KΦ)×KΦн/Uн=ϖ/f. (2.37)

Подставляя ν из (2.37) в (2.33) с учетом (2.24), получаем:

ηэ= 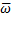=νf=1−μ/f. (2.38)

Подставляя в (2.38) полученные ранее предельные значения регулирующей координаты при известных значениях относительного момента, мы можем определить диапазон изменения к.п.д. двигателя.