
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Гидравлические потери по длине.
Потери напора по длине, иначе их называют потерями напора на трение 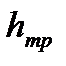 , в чистом виде, т.е. так, что нет никаких других потерь, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят и в шероховатых трубах, и в гладких. Величина этих потерь выражается зависимостью
, в чистом виде, т.е. так, что нет никаких других потерь, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят и в шероховатых трубах, и в гладких. Величина этих потерь выражается зависимостью
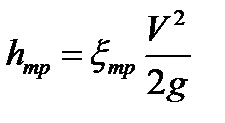 ,
,
где 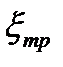 - коэффициент сопротивления, обусловленный трением по длине.
- коэффициент сопротивления, обусловленный трением по длине.
При равномерном движении жидкости на участке трубопровода постоянного диаметра d длиной l этот коэффициент сопротивления прямо пропорционален длине и обратно пропорционален диаметру трубы
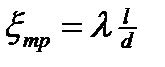 ,
,
где l– коэффициент гидравлического трения (иначе его называют коэффициент потерь на трение или коэффициент сопротивления трения).
Из этого выражения нетрудно видеть, что значение l - коэффициент трения участка круглой трубы, длина которого равна её диаметру.
С учетом последнего выражения для коэффициента сопротивления потери напора по длине выражаются формулойДарси
 .
.
Эту формулу можно применять не только для цилиндрических трубопроводов, но тогда надо выразить диаметр трубопровода d через гидравлический радиус потока 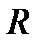
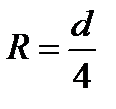 или
или 
где, напомним, ω – площадь живого сечения потока,
χ - смоченный периметр.
Гидравлический радиус можно вычислить для потока с любой формой сечения, и тогда формула Дарси принимает вид
 .
.
Эта формула справедлива как для ламинарного, так и для турбулентного режимов движения жидкости, однако коэффициент трения по длине λ не является величиной постоянной.
Запишем формулу Дарси-Вейсбаха в виде:
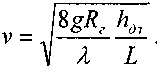
Величину 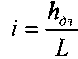 называют гидравлическим уклоном, а величину
называют гидравлическим уклоном, а величину 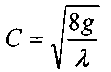 называют коэффициентом Шези.
называют коэффициентом Шези.
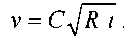
Величина  имеет размерность скорости и носит название динамической
имеет размерность скорости и носит название динамической
скорости жидкости.
Тогда коэффициент трения (коэффициент Дарси): 
Потери напора на трение в турбулентном потоке жидкости. При исследовании вопроса об определении коэффициента потерь напора на трение в гидравлически гладких трубах можно прийти к мнению, что этот коэффициент целиком зависит от числа Рей-нольдса. Известны эмпирические формулы для определения коэффициента трения, наиболее широкое распространение получила формула Блазиуса:
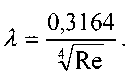
По данным многочисленных экспериментов формула Блазиуса подтверждается в пределах значений числа Рейнольдса от 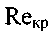 до 1-10 5. Другой распространённой эмпирической формулой для определения коэффициента Дарси является формула П.К. Конакова:
до 1-10 5. Другой распространённой эмпирической формулой для определения коэффициента Дарси является формула П.К. Конакова:

Формула П.К. Конакова имеет более широкий диапазон применения до значений числа Рейнольдса в несколько миллионов. Почти совпадающие значения по точности и области применения имеет формула Г.К. Филоненко:
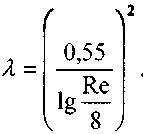
Изучение движения жидкости по шероховатым трубам в области, где потери напора определяются только шероховатостью стенок труб,  и не зависят от скорости движения жидкости, т.е. от числа Рейнольдса осуществлялось Прандтлем и Никурадзе. В результате их экспериментов на моделях с искусственной шероховатостью была установлена зависимость для коэффициента Дарси для этой так называемой квадратичной области течения жидкости:
и не зависят от скорости движения жидкости, т.е. от числа Рейнольдса осуществлялось Прандтлем и Никурадзе. В результате их экспериментов на моделях с искусственной шероховатостью была установлена зависимость для коэффициента Дарси для этой так называемой квадратичной области течения жидкости:
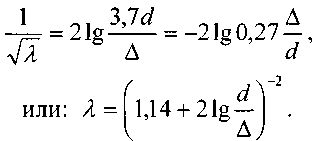
Для труб с естественной шероховатостью справедлива формула Шифринсона

где: 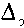 - эквивалентная величина выступов шероховатости. Ещё более сложная обстановка связана с изучением движения жидкости в переходной области течения, когда величина потерь напора зависит от обоих факторов,
- эквивалентная величина выступов шероховатости. Ещё более сложная обстановка связана с изучением движения жидкости в переходной области течения, когда величина потерь напора зависит от обоих факторов,
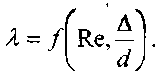
Наиболее приемлемых результатов добились Кёллебрук - Уайт:
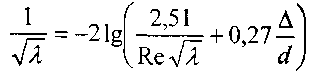
Несколько отличная формула получена Н.З. Френкелем:

Формула Френкеля хорошо согласуется с результатами экспериментов других авторов с отклонением (в пределах 2 - 3%). Позднее А.Д. Альтшуль получил простую и удобную для расчётов формулу:
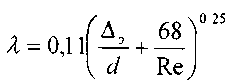
Обобщающие работы, направленные на унификацию результатов экспериментов, проведенных разными авторами, ставили перед собой цель связать воедино исследования потоков жидкости в самых разнообразных условиях.
Дата добавления: 2015-04-18; просмотров: 311; Мы поможем в написании вашей работы!; Нарушение авторских прав |