Уравнение Бернулли для стационарного потока жидкости

Уравнение Бернулли представляет собой закон сохранения энергии (другими словами, первый закон термодинамики) для потока жидкости.

Стационарным называется неускоренный поток жидкости, нестационарным – ускоренный.

Уравнение Бернулли справедливо для потока между двумя поперечным потоку сечениями жидкости:

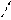
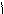
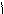
где 1 – индекс первого сечения; 2 – индекс второго сечения (рис. 5); P – абсолютное давление в сечении, Па; ρ·g·z- геометрическое давление в сечении, Па; a × r × u²/2– динамическое давление в сечении, Па; Р + r × g × z + a × r × u²/2 – полное давление в сечении (в первом всегда выше, чем во втором), Па; z – геометрическая высота центра сечения (вертикальная) над произвольной горизонтальной плоскостью, называемой плоскостью сравнения, м; α - коэффициент Кориолиса (для турбулентных потоков можно принять α = 1, а для ламинарных и структурных α = 2); u – средняя скорость потока в сечении, м/с; Р_тр – потеря давления на трение между сечениями, Па; Р_мех – механическое давление (давление, расходуемое жидкостью на работу забойного гидродвигателя, гидроударной машины, на вынос шлама из скважины и др.), Па.

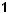
Рис. 5. Поток жидкости между сечениями 1 - 1 и 2 - 2:

а) – произвольный; б) – горизонтальный, постоянной площади сечения;
0 - 0 – плоскость сравнения; Н – длина потока.

В произвольном потоке (рис. 5а) соотношение давлений может быть различным: Р₁ > P₂, Р₁ = P₂ или Р₁ < P₂. Для случая, представленного на рис. 5б: Р₁ > P₂; u₁ = u₂.