Преобразование непрерывных сигналов в дискретные, их передача в виде цифровых сигналов.

ОТВЕТ:

Преобразование непрерывных сигналов в дискретные по амплитуде и времени сигналы (импульсно-кодовая модуляция). НВА – непрерывные по времени и амплитуде; ДАВ – дискретные по амплитуде и времени. Преобразование непрерывных сигналов в дискретные по амплитуде называется АЦП. 10→0123456789, 2→01. Дискретизация сигналов по амплитуде и времени позволяет передавать сигналы с помощью двоичного кода, обладающего

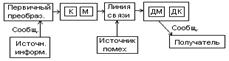
высокой помехоустойчивостью и обеспечивающего высокое качество передачи информационных сигналов. . Цифровой сигнал – последовательность 0 и 1. . Цифровые сигналы более помехоустойчивые

Ряд Фурье для периодической последовательности импульсов и его мощность. Амплитудно-частотная (АЧХ) и фазочастотная (ФХЧ) характеристики периодической последовательности импульсов.

ОТВЕТ:

Ряд Фурье – спектр сигналов. τ – длительность импульса, Т – период. . U(t)=U₀+U₁cos(w₁t+φ₁)+U₂cos(2w₁t+φ₂)+U₃cos(3w₁t+φ₃)+…+U_Ncos(nw₁t+φ_N). , n – номер гармоники, - круговая частота одной гармоники, U₀ – постоянная составляющая ряда Фурье. С увеличение номера гармоники амплитуда уменьшается. Чем больше взято членов разложения в ряд Фурье, тем ближе к идеальной форме прямоугольных импульсов будет предвычисленное значение. Ряд Фурье является аналитической формой представления периодических сигналов. . . . . . . . . В_N=0. φ_N=0. . , θ – скважность. , следовательно, . АЧХ – зависимость амплитуды выходного сигнала устройства от частоты входного сигнала, при постоянной амплитуде. ФЧХ – зависимость фазового сдвига между входным и выходным сигналом от частоты входного сигнала.