Магнитные цепи постоянного тока и методы их расчета

Расчет нелинейных магнитных цепей постоянного тока

Пусть задана нелинейная магнитная цепь (рис. 4.21). Габариты магнитной цепи заданы: сечение магнитопровода S, длина средней силовой линии l. Ток намагничивающей катушки I и ее число витков W также заданы

напряженность магнитного поля:

.

Если принять постоянной напряженность магнитного поля на всей длине L, то HL = IW или H = IW/L. магнитного потока: и учитывая, что магнитная индукция неизменна во всем сечении S, получим:

.

По характеристике намагничивания находим магнитную индукцию B.

Подставляем эту индукцию в формулу магнитного потока и находим его величину.

Таким образом, поставленная задача решена.

Рассмотренную магнитную цепь можно представить эквивалентной электрической цепью (рис. 4.23). В этой цепи F_m = IW – источник (магнитодвижущая сила). Магнитное сопротивление r_m можно определить по закону Ома:

.

1. Прямая” задача для неразветвленной магнитной цепи

Решение задач подобного типа осуществляется в следующей последовательности:

1. Намечается средняя линия (см. пунктирную линию на рис.1), которая затем делится на участки с одинаковым сечением магнитопровода.

2. Исходя из постоянства магнитного потока вдоль всей цепи, определяются значения индукции для каждого 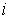-го участка:

.

3. По кривой намагничивания для каждого значения 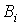находятся напряженности на ферромагнитных участках; напряженность поля в воздушном зазоре определяется согласно

4. По второму закону Кирхгофа для магнитной цепи определяется искомая НС путем суммирования падений магнитного напряжения вдоль контура:

,

где -длина воздушного зазора.

2. “Прямая” задача для разветвленной магнитной цепи

Расчет разветвленных магнитных цепей основан на совместном применении первого и второго законов Кирхгофа для магнитных цепей. Последовательность решения задач данного типа в целом соответствует рассмотренному выше алгоритму решения “прямой” задачи для неразветвленной цепи. При этом для определения магнитных потоков на участках магнитопровода, для которых магнитная напряженность известна или может быть вычислена на основании второго закона Кирхгофа, следует использовать алгоритм

по

В остальных случаях неизвестные магнитные потоки определяются на основании первого закона Кирхгофа для магнитных цепей.

В качестве примера анализа разветвленной магнитной цепи при заданных геометрии магнитной цепи на рис. 2 и характеристике ферромагнитного сердечника определим НС , необходимую для создания в воздушном зазоре индукции .

Алгоритм решения задачи следующий:

1. Задаем положительные направления магнитных потоков в стержнях магнитопровода (см. рис. 2).

2. Определяем напряженность в воздушном зазоре и по зависимости для - значение .

3. По второму закону Кирхгофа для правого контура можно записать

откуда находим и по зависимости - .

4. В соответствии с первым законом Кирхгофа

.

Тогда , и по зависимости определяем .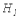

5. В соответствии со вторым законом Кирхгофа для искомой НС имеет место уравнение

.

Графические методы расчета

Графическими методами решаются задачи второго типа - “обратные” задачи. При этом в качестве исходных данных для расчета заданы конфигурация и геометрические размеры магнитной цепи, кривая (кривые) намагничивания ферромагнитного материала, а также НС обмоток. Требуется найти значения потоков (индукций) на отдельных участках магнитопровода.

Данные методы основаны на графическом представлении вебер-амперных характеристик линейных и нелинейных участков магнитной цепи с последующим решением алгебраических уравнений, записанных по законам Кирхгофа, с помощью соответствующих графических построений на плоскости.

Дата добавления: 2015-04-21; просмотров: 10; Нарушение авторских прав