
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основное уравнение МКТ
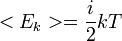 , где k является постоянной Больцмана (отношение универсальной газовой постоянной R к числу Авогадро NA), i — число степеней свободы молекул (
, где k является постоянной Больцмана (отношение универсальной газовой постоянной R к числу Авогадро NA), i — число степеней свободы молекул ( 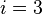 в большинстве задач про идеальные газы, где молекулы предполагаются сферами малого радиуса, физическим аналогом которых могут служить инертные газы), а T - абсолютная температура.
в большинстве задач про идеальные газы, где молекулы предполагаются сферами малого радиуса, физическим аналогом которых могут служить инертные газы), а T - абсолютная температура.
Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) газовой системы с микроскопическими (масса молекул, средняя скорость их движения).
[править]Вывод основного уравнения МКТ
Пусть имеется кубический сосуд с ребром длиной 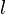 и одна частица массой
и одна частица массой  в нём.
в нём.
Обозначим скорость движения  , тогда перед столкновением со стенкой сосуда импульс частицы равен
, тогда перед столкновением со стенкой сосуда импульс частицы равен  , а после —
, а после —  , поэтому стенке передается импульс
, поэтому стенке передается импульс  . Время, через которое частица сталкивается с одной и той же стенкой, равно
. Время, через которое частица сталкивается с одной и той же стенкой, равно  .
.
Законы идеал-ого газа: 1) Бойля-Марриота- темпер-ра неизменна, изотер-ий процесс; 2) Гей-Люссака- изохорный, при постоянном объеме; 3) изобарный, при неизменном давлении газа. Закон Авогадро: При одинаковых условиях 1 моль любого газа занимает одинаковый объем; В одном моле любого вещ-ва содержится одинаковое число молекул. Закон Дальтона: Давление смеси газов, равно сумме порциональных давлений каждой составляющей в отдельности.
Б-5
| |
|
ИДЕАЛЬНЫЙ ГАЗ В ПОЛЕ СИЛЫ ТЯЖЕСТИ
Каково поведение идеального газа в поле внешней силы? Для определенности в качестве внешней силы возьмем хорошо известную силу тяжести mg. Под действием внешней силы механическая система частиц приобретает импульс и перемещается как целое поступательно в направлении силы. В идеальном газе, находящемся во внешнем поле сил, каждая отдельная частица приобретает импульс в направлении силы, а также соответствующую потенциальную энергию. Однако в газе наряду с упорядоченным движением в направлении действия силы существует хаотическое тепловое движение. В результате конкуренции между этими двумя типами движений возникает неравномерное распределение макроскопических параметров: плотности частиц, давления, температуры по объему, занимаемому газом.
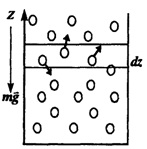
Рассмотрим столб газа сечением S, находящийся при постоянной температуре в поле силы тяжести. Выделим слой газа толщиной dzна высоте z и вычислим давление газа на его основания. Давление слоя газа на верхнее и нижнее основания слоя разное — оно различается в результате действия силы тяжести. Очевидно, разность давлений равна весу газа, заключенного в слое, отнесенному к единице площади основания столба.
Пусть разность давлений есть dP. Давление газа с ростом высоты уменьшается, поэтому dPравно весу слоя со знаком минус. Вес газа в объеме слоя dV= dz·Sравен ρ·g·dV, где ρ — плотность газа, g— ускорение силы тяжести. Таким образом,
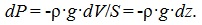
Дата добавления: 2015-04-21; просмотров: 420; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 откуда
откуда  Применяя методы теории вероятностей, Максвелл получил функцию f(ν) — закон о распределеня молекул идеального газа по скоростям:
Применяя методы теории вероятностей, Максвелл получил функцию f(ν) — закон о распределеня молекул идеального газа по скоростям:  (1) Из (1) видно, что конкретный вид функции зависит от вида газа (от массы молекулы) и от параметра состояния (от температуры Т). График функции (1) приведен на рис. 1. Так как при возрастании ν множитель exp[–m0ν2/(2kT)] уменьшается быстрее, чем увеличивается множитель ν2, то функция f(ν), начинаясь от нуля, достигает максимума при νB, и затем асимптотически стремится к нулю.
(1) Из (1) видно, что конкретный вид функции зависит от вида газа (от массы молекулы) и от параметра состояния (от температуры Т). График функции (1) приведен на рис. 1. Так как при возрастании ν множитель exp[–m0ν2/(2kT)] уменьшается быстрее, чем увеличивается множитель ν2, то функция f(ν), начинаясь от нуля, достигает максимума при νB, и затем асимптотически стремится к нулю.