Теорема Гаусса

[править]

Материал из Википедии — свободной энциклопедии

Классическая электродинамика

Электричество · Магнетизм

[показать]Электростатика   [показать]Магнитостатика   [показать]Электродинамика   [показать]Электрическая цепь   [показать]Ковариантная формулировка   [показать]Известные учёные

См. также: Портал:Физика

У этого термина существуют и другие значения, см. Теорема Гаусса (значения).

Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.

Аналогичная теорема, также входящая в число уравнений Максвелла, существует и для магнитного поля (см. ниже).

Также теорема Гаусса верна для любых полей, для которых верен закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, так как позволяет в частности вывести степень расстояния^[1] в законе Кулона «из первых принципов», а не постулировать ее (или не находить эмпирически).

В этом можно видеть фундаментальное значение теоремы Гаусса (закона Гаусса) в теоретической физике.

Существуют аналоги (обобщения) теоремы Гаусса и для более сложных полевых теорий, чем электродинамика.

Теорема Гаусса для напряжённости электрического поля в вакууме

Общая формулировка: Поток векторанапряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

СГС	СИ

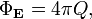
где

· — поток вектора напряжённости электрического поля через замкнутую поверхность .

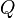· — полный заряд, содержащийся в объёме, который ограничивает поверхность .

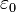· — электрическая постоянная.

Б-10

Связь напряжённости и потенциала электростатического поля

Потенциал и напряжённость — две локальные характеристики электростатического поля. То есть, это две характеристики — энергетическая и силовая — одной и той же точки поля.

Разумно предположить, что между ними должна существовать однозначная связь.

Для отыскания этой связи, вычислим работу электрической силы на элементарном перемещении dl заряда q в электростатическом поле 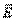(рис. 3.7.).

Рис. 3.7.

С одной стороны:

. (3.21)

Но с другой стороны, эту же работу можно связать с разностью потенциалов (j₁ – j₂) = –(j₂ – j₁) = –dj:

. (3.22)

Объединив (3.21) и (3.22), получим:

E_ldl = –dj.

Или:

. (3.23)

Важно отметить, что здесь E_l — проекция вектора напряжённости поля 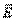на направление перемещения, а — изменение потенциала при переходе в поле из точки 1 в точку 2.

Записав (3.23) для направлений x, y и z, получим соответствующие составляющие (проекции) вектора напряжённости:

(3.24)

Первое уравнение этой системы означает, что проекция вектора напряжённости на ось x равна частной производной потенциала по x, взятой с противоположным знаком.

Полный вектор напряжённости можно, как обычно, представить в виде векторной суммы:

.

Последнее уравнение принято записывать так:

. (3.25)

Здесь векторный оператор «градиент» grad = .

Уравнение (3.25) устанавливает искомую связь двух характеристик электростатического поля — напряжённости и потенциала: напряжённость электростатического поля равна градиенту потенциала с обратным знаком.

До последнего времени мы измеряли напряжённость поля в :

.

Теперь, руководствуясь соотношением (3.23) можно получить ещё одну единицу измерения напряжённости:

.

Несложно показать, что эти две единицы измерения легко превращаются одна в другую:

Б-11

13. Конденсаторы. Электроемкость конденсатора. Применение конденсаторов

1. Определение конденсатора. 2. Обозначение. 3. Электроемкость конденсатора. 4. Электроемкость плоского конденсатора. 5. Применение конденсаторов. 6.Распространенные ошибки.

Для накопления значительных количеств разноименных электрических зарядов применяются конденсаторы. Конденсатор — это система двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Так, например, две плоские металлические пластины, расположенные параллельно и разделенные диэлектриком, образуют плоский конденсатор. Если пластинам плоского конденсатора сообщить равные по модулю заряды противоположного знака, то напряженность между пластинами будет в два раза Польше, чем напряженность одной пластины. Вне пластин напряженность равна нулю.

Обозначаются конденсаторы на схемах так:

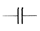— конденсатор постоянной емкости;

— конденсатор переменной емкости.

Электроемкостью конденсатора называют величину, равную отношению величины заряда одной из пластин к напряжению между ними. Электроемкость обозначается .

По определению . Единицей электроемкоести является фарад (Ф). 1 фарад — это электроемкость такого конденсатора, напряжение между обкладками которого равно 1 вольту при сообщении обкладкам разноименных зарядов по 1 кулону.

Электроемкость плоского конденсатора (рис. 16) находится по формуле:

,

где — электрическая постоянная, — диэлектрическая постоянная среды, — площадь обкладки конденсатора, — рас-стояние между обкладками (или толщина диэлектрика).

В зависимости от типа диэлектрика конденсаторы бывают воздушные, бумажные, слюдяные.

Конденсаторы применяются для накопления электрическоЙ энергии и использования ее при быстром разряде (фотовспышка), для разделения цепей постоянного и переменного тока, в выпрямителях, колебательных контурах и других радиоэлектронных устройствах.