Основы расчета газопроводов

При установившемся движении вязкого газа по трубе постоянного сечения, принимая во внимание постоянство массового расхода G, можно записать

Давление газа из-за трения уменьшается вдоль потока. При этом газ расширяется, а его плотность уменьшается, что приводит к росту скорости течения, как видно из вышеприведенной формулы.

При полном отсутствии теплообмена с окружающей средой процесс расширения при движении газа будет адиабатным, а при интенсивном теплообмене температура газа вдоль трубы остается постоянной, т.е. происходит изотермический процесс. Чем короче трубопровод, тем ближе процесс к адиабатному, и наоборот, для длинных трубопроводов более характерным является изотермический процесс.

Выразим критерий Рейнольдса для потока газа через массовый расход газа и коэффициент динамической вязкости:

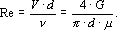
Из данного выражения видно, что критерий Рейнольдса может изменяться вдоль потока лишь за счет изменения динамической вязкости. Но вязкость газов не зависит от давления, а определяется лишь температурой, поэтому при изотермическом процессе движения газа по трубопроводу критерий Рейнольдса будет оставаться постоянным вдоль потока. Следовательно, коэффициент потерь на трение l также будет величиной постоянной вдоль трубы постоянного диаметра, несмотря на возрастание скорости потока газа.

Рассмотрим изотермическое течение газа по трубопроводу постоянного сечения. Выделим элементарный объем газа, заключенный между двумя сечениями, отстоящими друг от друга на расстояние dx. Обозначение характеристик трубопровода и потока приведены на рис. 5.4.1.

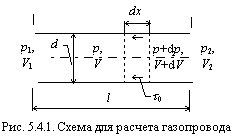
Применим к выделенному объему теорему об изменении количества движения. Приращение за единицу времени количества движения в направлении потока представим в виде

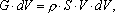
где S - площадь поперечного сечения трубопровода.

Это приращение получается в результате действия импульса внешних сил dR (сил давления и трения) за тот же промежуток времени.

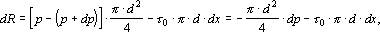
где t0 - касательное напряжение на стенке трубы.

Приравнивая, на основании теоремы об изменении количества движения, последние два уравнения, получаем

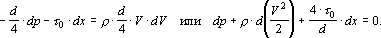
Используя формулу, связывающую касательные напряжения с потерями давления в результате трения газа о стенки, преобразуем предыдущую зависимость к виду

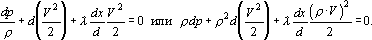
В начале главы показано, что произведение плотности на скорость движения газа есть величина постоянная, следовательно

поэтому предыдущее уравнение можно переписать в виде

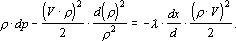
Используя уравнение состояния идеального газа [ ], вместо последнего уравнения получим

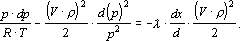
Так как по условию температура газа не меняется, можно выполнить интегрирование вдоль газопровода, т.е. в пределах от p1 до p и соответственно от x=0 до x=l. В результате получим

Отсюда определяем массовый расход газа

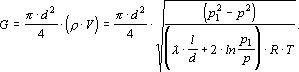
В длинных трубопроводах при движении газа со скоростями, значительно меньшими звуковых

В этих условиях формула для определения массового расхода газа упрощается

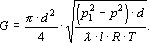
Коэффициент l, входящий в вышеприведенные формулы, определяется, как и для жидкости, по критерию Рейнольдса и относительной шероховатости трубопровода.