Расчет водозаборного регулятора .

Расчет сводится к определению его ширины 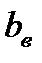и толщины , при которых перед сооружением сохраняется нормальная глубина.

В качестве регулятора выберем водослив с широким порогом с прямоугольным входным ребром, сопряжение которого с магистральным каналом осуществляется по типу конусов

Приложение 8

Определим коэффициент расхода m для данного водослива по формуле Березинского

-геометрический напор на водослив

-высота водослива со стороны верхнего бьефа

Примем, что , тогда

H=h_max+∆z-P=1.96+0.45-0.7=1. 71м

h_max=h_б=1.96м

- снижение ГВ в магистральном канале у регулятора при максимальной глубине

, м/с

где Q_max – максимальный расход через поперечное сечение площадью

м²

где,

b - ширина магистрального канала

m – коэффициент заложения откосов, зависящий от грунта

Подставив числовые значения получаем:

*1.96=17.35

м/с

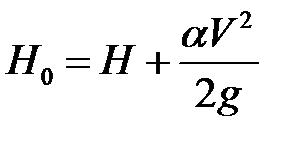
Определим, является ли водослив подтопленным или неподтопленным.

Для этого находим глубину полтопления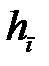

м

м

Водослив считается подтопленным если ,

1.26>1.16

следовательно водослив подтоплен . Из соотношения h_п /H₀ находим -коэфициент подтопления , воспользуемся [1. 6-24 ,стр 70],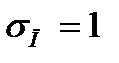

Определяем b₁ :

где

Q – максимальный расход

п– коэффициент подтопления

- коэффициент сжатия

m – коэффициент расхода

<

4.12м<5,91м

Определяем δ в диапазоне 2H<δ<8H. Принимаем δ=4*H=6.8м