
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Истечение жидкости через отверстие (или насадок) при постоянном уровне
Для вывода уравнений расхода и скорости истечения через отверстие и насадок при постоянном уровне запишем уравнение Бернулли для идеальной жидкости для двух живых сечений 1–1 (на свободной поверхности жидкости в сосуде) и 2–2, за плоскость сравнения примем сечение 2–2, (рисунок 29):

| |
| Рисунок 29 – К выводу уравнений расхода и скорости истечения жидкости через отверстие |
 ,
,
Тогда z1= H , z2=0.
Скоростью в сечении 1-1  , скорость в сечении 2-2
, скорость в сечении 2-2  (
(  - теоретическая скорость истечения жидкости).
- теоретическая скорость истечения жидкости).
 ,
,
Тогда  и
и 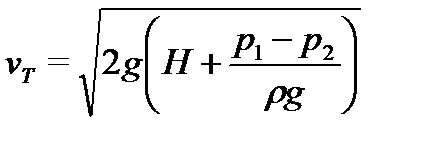 .
.
Пусть у поверхности жидкости в резервуаре, давление равно атмосферному и истечение через отверстие происходит в пространство с атмосферным давлением, то есть p1 = p2 = pатм .
И теоретическая скорость истечения в этом случае рассчитывается:
 .
.
Эта формула была получена Эванджелиста Торричелли, в 1643 году.
Для реальной жидкости учитываются потери напора в сечении 2-2. Они обусловлены потерей напора hп на местном сопротивлении и определяются по формуле:
 ,
,
где ζ -коэффициент местного сопротивления (для входа в трубу без закругленных кромок ζ= 0,5, а с закругленными кромками ζ= 0,1).
Тогда формула для расчета действительной скорости истечения через отверстие будет выглядеть следующим образом:
 ,
,
Величина  называется коэффициентом скорости и обозначается через φ.
называется коэффициентом скорости и обозначается через φ.
Коэффициент скорости φ представляет собой отношение действительной скорости истечения к теоретической, определяется опытным путем.
Таким образом, действительная скорость истечения реальной жидкости:
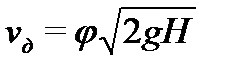 ,
,
Зная скорость истечения жидкости можно определить расход жидкости через отверстие:
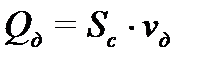 ,
,
где 
Подставляя значения, для скорости и коэффициента сжатия получаем:
 ,
,
где ε – коэффициент сжатия струи,
S0 – площадь отверстия,
φ – коэффициент скорости,
Произведение коэффициента сжатия струи на коэффициент скорости называется коэффициентом расхода и обозначается μр. Следовательно:
 ,
,
Коэффициентом расхода μр называется отношение действительного расхода к теоретическому:
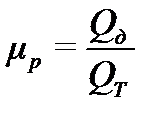 ,
,
Тогда
 ,
,
 ,
,
При истечении через малое отверстие в тонкой стенке коэффициент скорости φ с увеличением Re возрастает, что связано с уменьшение сил вязкости, что в свою очередь сказывается на уменьшении коэффициента сопротивления ξ.
Коэффициент сжатия струи на выходе из насадка ε=1, что приводит к повышению значения коэффициента расхода μр и соответственно расхода жидкости.
Средние значения коэффициентов истечения ε, φ, μр, ξ для малых отверстий в тонкой стенке и насадка при числах Re больше 105 приведены в таблице 2.
Таблица 2 - Основные гидравлические характеристики для малых отверстий и насадка при числах Re>105
| Тип насадка или отверстия | Коэффициенты | |||
| ε | φ | μр | ξ | |
| Отверстие в тонкой стенке | 0,62÷0,64 | 0,97 | 0,6÷0,62 | 0,06 |
| Внешний цилиндрический насадок | 1,0 | 0,82 | 0,82 | 0,5 |
В случаях, когда число Re меньше 105, коэффициенты истечения находят из графика А.Д. Альтшуля (рисунок 30), составленного на основании опытов разных авторов.

Рисунок 30 – Зависимость коэффициента расхода от значения критерия Рейнольдса для круглого отверстия
Из графика следует, что с увеличением числа Re коэффициент расхода μр сначала увеличивается, а затем, достигнув максимального значения μр = 0,69 при Re = 350, уменьшается и стабилизируется на значении, близком к μр = 0,62. Таким образом, коэффициенты истечения при достаточно больших числах Re зависят только от формы отверстий и насадков [2-4,10].
Дата добавления: 2015-04-18; просмотров: 386; Мы поможем в написании вашей работы!; Нарушение авторских прав |