
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Местные сопротивления. В местных гидравлических сопротивлениях, вследствие изменения конфигурации потока на коротких участках
В местных гидравлических сопротивлениях, вследствие изменения конфигурации потока на коротких участках, изменяются скорости движения жидкости по величине и направлению, а также образуются вихри. Это и есть причиной местных потерь напора. Местными сопротивлениями являются расширения и сужения русла, поворот, диафрагма, вентиль, кран и т.п. (рис.4.3).
Потери напора в местных сопротивлениях определяются по формуле (4.4).
При турбулентном режиме коэффициент  зависит в основном от вида местного сопротивления, а при ламинарном- от числа Рейнольдса. Для всех местных сопротивлений этот коэффициент определяется экспериментально .
зависит в основном от вида местного сопротивления, а при ламинарном- от числа Рейнольдса. Для всех местных сопротивлений этот коэффициент определяется экспериментально .

|
| Рисунок 4.3 – Местные гидравлические сопротивления: а – задвижка; б – диафрагма; в – поворот; г – вентиль |
Рассмотрим некоторые местные сопротивления.
Внезапное (резкое) расширение трубы (рис.4.4).

| При внезапном расширении трубы поток срывается с угла и постепенно расширяется. Между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии. Потери напора в этом случае определяют по теореме Борда |
| Рисунок 4.4 – Внезапное расширение трубы |
 (4.10)
(4.10)
где 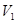 и
и  - скорость жидкости впереди и после внезапного сужения.
- скорость жидкости впереди и после внезапного сужения.
Формулу (4.9) можно записать в виде:
 . (4.11)
. (4.11)
При этом для скорости 
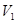
 . (4.13)
. (4.13)
При выходе жидкости из трубы в резервуар возникает резкое расширение потока. В этом случае 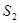 >>
>> 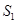 (площадь резервуара значительно больше площади трубы).Коэффициент потерь на выходе из трубы будет:
(площадь резервуара значительно больше площади трубы).Коэффициент потерь на выходе из трубы будет:  =1.
=1.
Внезапное сужение трубы (рис 4.5) вызывает меньшие потери энергии, чем внезапное расширение. В этом случае потери обусловлены трением потока при входе в узкую трубу и потерями на вихреобразование. Потери напора при внезапном сужении трубы определяют по формуле
 (4.13)
(4.13)
где  определяется по формуле Идельчика
определяется по формуле Идельчика



|
| Рисунок 4.5 – Внезапное сужение трубы |
При входе жидкости из резервуара в трубу можно считать  , а коэффициент сопротивления равным
, а коэффициент сопротивления равным  Поворот трубы (рис 4.6) или колено без закругления вызывает
Поворот трубы (рис 4.6) или колено без закругления вызывает

| значительные потери энергии, так как в нем происходят отрыв и вихреобразование, причем тем больше ,чем больше  .Потерю напора рассчитывают по формуле .Потерю напора рассчитывают по формуле
 (4.14) (4.14)
|
| Рисунок 4.6 – Поворот трубы |
где  - коэффициент сопротивления колена, который определяется по справочным данным.
- коэффициент сопротивления колена, который определяется по справочным данным.
Дата добавления: 2015-04-18; просмотров: 230; Мы поможем в написании вашей работы!; Нарушение авторских прав |