Введение. Биологический факультет

ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Биологический факультет

Кафедра биотехнологии

К.О. Камалов, Ф.И. Ахмаров, А.А. Токарев

ПРИКЛАДНАЯ ГИДРАВЛИКА

(Гидродинамика)

Методические указания

к лабораторным работам

Дисц. «Процессы и аппараты

химической технологии»

«Гидравлика и теплотехника»

Киров 2009

Печатается по решению редакционно-издательского совета

Вятского государственного университета

УДК 66.011(075.6)

К 18

Рецензент: Кандидат химических наук, доцент В.И.Вшивцев

Камалов К.О., Ахмаров Ф.И., Токарев А.А. Прикладная гидравлика (Гидродинамика): Методические указания к лабораторным работам / К.О.Камалов и др. – Киров: Изд-во ГОУ ВПО «ВятГУ», 2009. -28с.

Содержание:

Введение. 4

Лабораторная работа № 1. Демонстрация режимов течения жидкости. Определение критерия Рейнольдса. 8

Лабораторная работа № 2. Демонстрация уравнения Бернулли. Построение линии полного гидродинамического напора. Определение величины потерянного напора 11

Лабораторная работа № 4. Потери напора на трение. Определение коэффициента трения и абсолютной эквивалентной шероховатости. 19

Приложение 1. 23

Приложение 2. 24

Приложение 3. 25

Приложение 4. 26

Приложение 5. 27

Библиографический список. 28

Введение

Гидравлика -это наука о законах равновесия и движения жидкостей. Она состоит из двух разделов: гидростатики и гидродинамики.

Гидростатика рассматривает законы равновесия жидкостей в состоянии покоя.

Гидродинамика изучает законы движения жидкостей.

Теоретические положения и уравнения гидродинамики основаны на главных физических законах: законе сохранения энергии и законе сохранения массы. Они сводятся к двум уравнениям: основному уравнению гидродинамики (уравнение Бернулли) и уравнению сплошности (неразрывности) потока.

Подсчитаем механическую энергию потока жидкости. Для этого выделим в потоке жидкости некий объем с массой m(кг) и весом mg(Н), движущийся по трубопроводу со скоростью w (м/с), и подсчитаем запас энергии, которым он обладает.

1 – трубопровод; 2 – пьезометр

3- манометр; 4 – выделенный объем

жидкости; z – расстояние центра

тяжести потока от плоскости

сравнения; h – показание

пьезометра, м

Рис.1

Механическая энергия потока жидкости складывается из:

- потенциальной энергии положения, равной

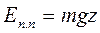; [ Е_п.п ]_Си = [кгּм/с²ּм] = [Нּм] = [Дж];

- потенциальной энергии давления (Е_{п. д}), равной

; [ Е_{п. д} ]_Си = [ кгּм/с²ּм] = [Нּм] = [Дж];

- кинетической энергии (Е_к), равной

; [ Е_к ] = [кгּм²/с²] = [кгּм/с²ּм] =[Нּм] =[Дж].

Тогда полная энергия потока будет равна:

.

Относя эту величину к единице веса (mg), получим значение полной удельной энергии потока (е_уд)

.

Учитывая, что значения давления, выраженные в высоте столба жидкости h(м) и в Па (Н/м² ), связаны между собой зависимостью р = ρgh , то h = р / ρg . Следовательно, можно записать: ,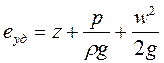

где z – геометрический напор, удельная потенциальная энергия положения, м;

р/ ρg – пьезометрический напор, удельная потенциальная энергия

давления, м;

- статический напор, м;

w²/2g – динамический (скоростной) напор, удельная кинетическая энергия,

м;

- полный гидродинамический напор, полная удельная

энергия потока, м.

Для идеальной жидкости, т.е. жидкости, не обладающей вязкостью, из закона сохранения энергии следует, что величина полного гидродинамического напора для различных сечений потока остается величиной постоянной:

.

Это уравнение носит имя Бернулли (строгое доказательство этого равенства смотри в лекционном курсе). Из него следует, что при изменении поперечного сечения трубопровода (и соответственно скорости потока) происходит взаимное превращение энергии: при сужении трубопровода часть потенциальной энергии давления переходит в кинетическую, и, наоборот, при расширении трубопровода часть кинетической энергии переходит в потенциальную, однако общее количество энергии (полный гидродинамический напор) остается постоянным. Это равенство сохраняется и при изменении геометрического напора в различных сечениях трубопровода.

При течении по трубопроводам реальных (вязких) жидкостей имеют место потери напора (давления), которые обуславливаются двумя факторами: сопротивлением трения и так называемыми местными сопротивлениями.

Сопротивление трения возникает в результате действия сил внешнего трения о стенки трубопровода. Потери напора на трение (h _тр ) имеют место в равномерном потоке, распределены по всей длине трубопровода и зависят от режима течения потока и шероховатости внутренней стенки трубопровода.

Местные сопротивления возникают при любых изменениях скорости потока, обусловленных изменением его сечения, или при изменениях его направления (внезапное сужение, расширение, кран, диафрагма, поворот и т.п.). В этих местах трубопровода образуются мертвые зоны, в которых возникают замкнутые вихри, на образование которых затрачивается механическая энергия потока (h _м.с).

В реальных гидросистемах участки равномерного движения, как правило, чередуются с местными сопротивлениями. Если местные сопротивления разделены участками равномерного движения, т.е. не влияют друг на друга, то при подсчете полных потерь напора может быть применен принцип сложения (аддитивности).

Сумму потерь напора на трение и местные сопротивления называют потерянным напором (h _пот = h _тр + h _м.с). Название это условное, так как указанная часть энергии не «теряется», а переходит в тепловую и общий баланс энергии сохраняется. С учетом этого обстоятельства в уравнение Бернулли для реальной (вязкой) жидкости необходимо ввести член, учитывающий величину потерянного напора:

либо ,

либо .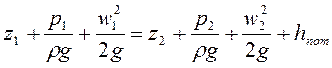

Определение величины потерянного напора является центральной задачей прикладной гидравлики.

Потери напора на трение и местные сопротивления выражают в долях от скоростного напора:

(1)

где λ – коэффициент трения;

l – длина трубопровода, м;

d – внутренний диаметр трубопровода, м ( в случае трубы некруглого сечения берется d_экв);

w²/2g - скоростной напор, м (w_ср).

(2)

где ξ_м.с - коэффициент местного сопротивления (справочник);

w²/2g - скоростной напор, м (в данном случае при расчете скоростного напора w берется для узкого сечения потока).

При движении жидкостей по трубам и каналам различают два режима течения: ламинарный и турбулентный. Ламинарное течение характеризуется тем, что частицы жидкости движутся по прямолинейным параллельным траекториям без перемешивания жидкости. В турбулентном потоке частицы движутся беспорядочно, хаотично. Наряду с поступательным движением происходят поперечные перемещения и вращательное движение частиц, которые приводят к интенсивному перемешиванию жидкости. Переход от ламинарного движения к турбулентному происходит внезапно при достижении некоторым безразмерным комплексом физических величин критического значения. Этот комплекс называется критерием Рейнольдса и имеет вид ,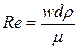

где w – средняя скорость потока, м/с;

d – внутренний диаметр трубопровода, м (в случае трубы некруглого сечения берется d_экв);

ρ – плотность жидкости, кг/м³;

μ – динамическая вязкость жидкости, кг/м·с.

Для трубы круглого сечения критическое значение критерия Re = 2320. При числах Re ниже этой величины течение ламинарное, выше этого значения -турбулентное. Причем это критическое значение числа Re не зависит от рода жидкости (ρ, μ) и диаметра трубопровода.

Величина коэффициента трения (λ) в формуле (1) зависит от режима течения жидкости и состояния внутренней поверхности трубы:

где d – внутренний диаметр трубопровода, м (в случае трубы некруглого сече-

ния берется d_экв);

e – абсолютная эквивалентная шероховатость, м.

Эта зависимость приведена в приложении 1 (рис.1), средние значения абсолютной шероховатости – в приложении 2.

Значения коэффициентов местных сопротивлений зависит как от геометрии сопротивления, так и от режима течения:

ξ _м.с = f (геом, Re) и приведены в справочной литературе [1].

В лабораторный практикум по гидродинамике входят четыре лабораторные работы:

- работа № 1: «Демонстрация режимов течения жидкости. Определение

критерия Рейнольдса»;

- работа № 2: «Демонстрация уравнения Бернулли. Построение линии

полного гидродинамического напора»;

- работа № 3: «Потери напора на местные сопротивления. Определение

потерь напора при внезапном расширении трубы и

коэффициента местного сопротивления»;

- работа № 4: «Потери напора на трение. Определение коэффициента

трения и абсолютной эквивалентной шероховатости».