Теоретическое обоснование

Гидравлические сопротивления делятся на сопротивления сил вязкостного трения по длине трубы и местные сопротивления.

Потери напора на трение рассмотрены для случая равномерного движения жидкости, т.е. живое сечение вдоль трубы сохраняется постоянным. При движении жидкости в местных сопротивлениях поток претерпевает деформацию, что приводит к изменению форм и размеров живого сечения, и. следовательно, движение жидкости становится неравномерным, вследствие чего происходит изменение скорости потока. В местах изменения живого сечения или направления потока происходит его отрыв от стенок, и образуются так называемые вихревые или застойные зоны. Между основным потоком и вихревыми зонами осуществляется интенсивный обмен частицами жидкости, что является основным источником местных потерь энергии.

Количество энергии (напора), затрачиваемой на преодоление местных сопротивлений в напорных трубах (внезапное сужение и расширение, резкий поворот потока и т.д.) в большинстве случаев определяется с помощью коэффициентов, полученных опытным путем.

Потери напора в местных сопротивлениях при турбулентном режиме вычисляют по формуле Вейсбаха:

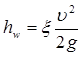(4.1)

где - безразмерный коэффициент местного сопротивления,

- средняя скорость потока за местным сопротивлением.

Таким образом, местные потери напора пропорциональны скоростному напору.

Значения коэффициентов местного сопротивления получают экспериментально из формулы (4.1)

(4.2)

Если местное сопротивление (например, вентиль, диафрагма, колено и т.п.) расположено на горизонтальном трубопроводе постоянного сечения, то потери напора будут равны разности показаний пьезометров, установленных по обе стороны местного сопротивления.

Т.к. 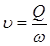, то, подставляя это значение в формулу 4.2, получим формулу для определения коэффициента сопротивления опытным путём:

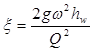(4.3)

где 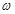– площадь сечения трубопровода до сопротивления.

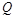– расход жидкости через сопротивление.

Ввиду сложности явлений, происходящих в жидкости при движении через местные сопротивления, теоретические формулы для определения потерь напора и коэффициентов местных сопротивлений удалось получить только для простейших видов, таких как внезапное расширение и сужение, плавное расширение или сужение, диафрагма и т.п.