Уравнение Тейса, квазистационарный режим фильтрации, учет переменного дебита скважин. Особенности восстановления уровня.

Квазистационарный режим – нестационарный режим, но в каждый момент времени можно считать стационарным. В нашем случае, если дебит постоянный, то в напорном изолированном пласте воронка депрессии будет опускаться параллельно самой себе. В напорном изолированом пласте этот режим обуславливается проявлениями упругой емкости.

Уравнение Тейса – это решение для уравнения фильтрации в напорном изолированом , неограниченом в плане пласте при откачке из совершенной скважины с постоянным дебитом Q, начиная с момента времени t0 при исходном стационарном потоке.

, где s – понижение, pi-число пи, T – проводимость, 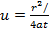, опять же где r – радиальная координата, a – пьезопроводность, t – время с начала откачки.

Если u меньше 0.09 то имеет логарифмическое представление ln( )

Данное уравнение можно очень широко пользовать, для примера можно рассчитать какой нужен куст скважин, если знаем примерную проводимость или наоборот, проводимость по откачке посчитать =)))))

Это решение можно распространить на случай ступенчатого изменения дебитаиспользуя принцип суперпозиции.

На первую ступень накладывается вторая ступень.

+ ,

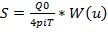Заметьте, там когда суперпозируешь, не Q1, а разница второго расхода и первого, дельта Q.

u1=

Исходя из принципа суперпозиции точно так же можно получить уравнение постановления уровня, тогда просто в качестве прибавляемого расхода выступает отрицательный расход откачки.

Вопрос 14. Формы массопереноса в водоносных породах. Конвективный перенос, диффузия, дисперсия и сорбция мигрантов в однородной и неоднородной геофильтрационных схемах.

Массоперенос представляет собой процесс перемещения растворенных в подземных водах компонентов и является гидрогеодинамической частью процессов геомиграции, которые изменяют химический состав подземных вод.

Однако массоперенос нельзя не рассматривать без процессов физико-химических обменов в системе “вода-порода”.

Далее будем рассматривать перенос одного компонента химического состава подземных вод. Его содержание (объемную концентрацию) в подземных водах будем обозначать C, размерность [масса/ объем] и выражается обычно в гр, мг, молях на литр, кубометр и т.д. Этот же компонент может содержаться и в твердой фазе (породы). Его содержание в твердой фазебудем обозначать N, полагая, что N – это объемное содержание компонента в породе (гр, мг на единицу объема породы). Другое, часто используемое в почвоведении, грунтоведении и др. отраслях обозначение для содержания компонента в твердой фазе – это его содержание, рассчитанное на единицу веса твердой фазы Nв. Очевидно, что Nв=N/γп. Где γп.- объемный вес породы. Основными процессами обмена содержащихся в твердой фазе и жидкой фазе компонентов являются растворение-осаждение, сорбционный обмен, выщелачивание. Важную роль в миграции играют процессы сорбционного обмена, включающие все виды сорбции (физическую, химическую, ионный обмен). Далее буде рассматривать процессы однокомпонентного обмена- то есть процессы, в которых концентрация других компонентов растворенных в подземных водах и находящихся в породе не влияет на обмен исследуемого компонента, либо это влияние постоянно для рассматриваемых условий – данной физико-химической обстановке. Сорбционное равновесие. Важным положением теории сорбции является понятие сорбционного равновесия. Это означает, что при контакте воды, содержащий исследуемый компонент с породой между ними возникает сорбционное равновесие – то есть некоторой концентрации компонента в воде C соответствует равновесная ей концентрация в породе N. Связь между С и N называется изотермой сорбции. Наиболее известны и теоретически обоснованы следующие изотермы сорбции: Изотерма Генри (линейная изотерма): N = Kd*C – закон действующих масс, где Kd – коэффициент распределения.

Согласно, данной изотерме – связь между содержанием компонента в твердой и жидкой фазах линейна и нет никаких ограничений на сорбцию компонента в твердой фазе. Однако, известно, что эта связь часто бывает нелинейна, часто с увеличением концентраций в породе происходит нелинейное изменение содержания этого мигранта в твердой фазе. Одной из теоретически обоснованных моделей такого изменения является изотерма сорбции Фрейндлиха, которая имеет вид: N = Kd*Cⁿ , где, n – параметр изотермы (чаще всего он меньше 1).

Кинетика сорбции. Для наступления сорбционного равновесия требуется некоторое время. Для описания неравновесного процесса часто используется простейшее уравнение кинетики сорбции, которое имеет вид: dN/dt = α (С - С∞), где α – константа кинетики, имеющая размерность обратную времени [1/T], а концентрация C∞ – содержание мигранта соответствующее равновесному состоянию, согласно изотерме сорбции (например, для изотермы Генри эта концентрация равна N/Kd).

Кинетика сорбции оказывается важной только для времен, имеющих порядок 1/ α и меньше, а для больших времен она несущественна. Результаты экспериментов показывает, что в ряде случаев сорбционных процессов величина α составляет сотни сут^-1. То есть кинетика интересна для процессов, имеющих масштаб времени часы и менее. Однако существуют данные, что только часть вещества сорбируется быстро, а часть достаточно долго.

Конвективный перенос – это гидравлический перенос исследуемого компонента (мигранта) с потоком подземных вод, имеющим действительную скорость u. Действительная скорость u = V/n₀, где V – скорость фильтрации, n₀ - активная пористость.

Рассмотрим баланс вещества в трубке тока при передвижении границы на dl.

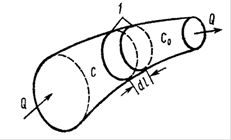ω – площадь поперечного сечения

В этот элемент через левую входит масса вещества с потоком с концентрацией С*Qdt, а выходит C₀Qdt, а остается в воде ωndl(C-C₀) и на породе ωdl(N-N₀):

(С - С₀) Qdt = ωdl (n (С – С₀) + (N-N₀))

Скорость конвективного переноса равна отношению скорости фильтрации к параметру, который В.М. Шестаков назвал эффективной пористостью:

u = V/n_эф ; n_эф = n + dN/dC.

Другой способ определения скорости задержки сорбируемого компонента состоит во введение параметра задержки R (retention factor), определяемого как: R = 1+ Kd/n (если R>1 то есть замедление; R=1, то нет замедления).

Связь между скоростью фильтрации и миграции определяется как: u = V/ nR.

Смысл величины R - во сколько раз медленнее движется сорбируемый мигрант, чем нейтральный.

Переносимый мигрант может рассеиваться в потоке подземных вод за счет диффузии и дисперсии. Диффузионный поток определяется законом Фика: V_d = - D_м dC/dl, связывающий диффузионный поток V_d – скорость диффузии, с градиентом концентрации мигранта dC/dl и в который в качестве коэффициента входит коэффициент диффузии D_м.

Дисперсионное рассеивание на микроуровне зависит от неравномерности локального поля скоростей потока в пористой среде.

Исследования гидрогеохимической миграции в значительной мере определялись практическими потребностями в количественном обосновании условий загрязнения подземных вод, включая управление их развитием, особенно в зоне влияния водозаборов, при складировании и захоронении промышленных отходов.