
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные законы движения газа
Закон сохранения массы при установившемся течении газа в трубке тока выражается в постоянстве массового расхода QM:
QМ = r1u1s1=r2u2s2 = const. (4.1)
Здесь s1, s2 - площади сечений, u1, u2 и p1, p2 — средние в этих сечениях скорости и плотности соответственно.
Закон изменения количества движения для установившегося течения газа в трубке тока при равномерном распределении параметров по сечению имеет вид
 (4.2)
(4.2)
где  — главный вектор сил давления, действующих в сечениях 1 и 2 со стороны окружающей жидкости;
— главный вектор сил давления, действующих в сечениях 1 и 2 со стороны окружающей жидкости;  — главный вектор сил трения, действующих по поверхности объема газа между сечениями 1 и 2;
— главный вектор сил трения, действующих по поверхности объема газа между сечениями 1 и 2;  — главный вектор массовых сил, приложенных к тому же объему;
— главный вектор массовых сил, приложенных к тому же объему;  —главный вектор реакции твердых тел, с которыми соприкасается выделенный объем.
—главный вектор реакции твердых тел, с которыми соприкасается выделенный объем.
Закон сохранения полной энергии при установившемся течении газа в трубке тока с равномерным распределением параметров в сечениях 1 и 2 записывается в виде
 (4.3)
(4.3)
где z1, z2 — вертикальные координаты центров сечений; i1, i2 — энтальпии в тех же сечениях; К (е) - подведенная извне тепловая мощность; N(е)) — подведенная механическая мощность. Для совершенного газа при пренебрежении действием силы тяжести уравнение (4.3) имеет вид
 (4.4)
(4.4)
или
 (4.5)
(4.5)
Для энергетически изолированной системы К (е)=0, N (е)=0, и уравнения (4.4) , (4.5) принимают вид
 (4.6)
(4.6)

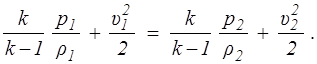 (4.7)
(4.7)
Обозначим через T0, р0, r0, i0 параметры торможения, т.е. значения соответственно температуры, давления, плотности и энтальпии в данном поперечном сечении, получаемые при воображаемом изэнтропическом (при отсутствии трения и теплообмена) уменьшении скорости потока до нуля.
Закон сохранения полной энергии для энергетически изолированного потока совершенного газа, записанный с помощью параметров торможения, имеет вид
 (4.8)
(4.8)
или

 (4.9)
(4.9)
Для адиабатического изэнтропического потока газа все параметры торможения остаются постоянными по длине потока. Для адиабатического потока с трением, для которого энтропия вдоль потока меняется, параметры торможения р0 , r0 будут различными в разных сечениях, а температура торможения Т0, энтальпия торможения i0 и отношение р0 /r0 остаются вдоль потока постоянными.
Для энергетически неизолированного потока при N(e) = 0 подведенная внешняя теплота, рассчитанная на единицу массы, равная q = К(е)/QM, определяется из уравнения (4.4):
 (4.10)
(4.10)
Уравнение закона сохранения энергии в механической форме для элемента струйки сжимаемой вязкой среды между двумя сечениями, расположенными на бесконечно малом расстоянии друг от друга, имеет вид
 (4.11)
(4.11)
где dh — потеря удельной энергии за счет трения.
Мощность идеального компрессора и идеальной турбины (К(е) = 0) определяется по формуле

 (4.12)
(4.12)
или

 (4.13)
(4.13)
где индексом "01" обозначены параметры торможения до машины; индексом "02" - после машины; μ - 1 кмоль газа.
Отклонение от изэнтропического процесса в машине учитывается обычно при помощи дополнительного множителя, представляющего собой к.п.д. машины η. В случае компрессора получим
LK = L/h;
в случае турбины
LT = hL.
Полезная мощность компрессора или затрачиваемая мощность турбин
N(e) = QML =r01 Q01 L. (4.14)
где Q01 — объемный расход газа при р01 и ρ01 .
Вопросы по теме 4.
1. Как записать закон сохранения массы при установившемся течении газа в трубке тока?
2. Что понимается под параметрами торможения газа?
3. Как изменяются параметры торможения по длине потока при адиабатическом, изэнтропическом течении газа в трубке тока?
4. Что происходит с температурой идеального совершенного газа с ростом скорости при установившемся адиабатическом течении в трубке тока?
Дата добавления: 2015-04-18; просмотров: 344; Мы поможем в написании вашей работы!; Нарушение авторских прав |