
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Элементы квантовой механики
Страница 1 из 4
38. Определите импульс и энергию: 1) рентгеновского фотона; 2) электрона, если длина волны того и другого равна 1010 м.
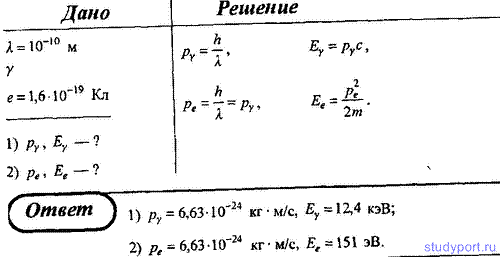
39. Определите длину волны де Бройля для электрона, находящегося в атоме водорода на третьей боровской орбите.

40. Определите длину волны де Бройля для нейтрона, движущегося со средней квадратичной скоростью при T = 290 К.

41. Протон движется в однородном магнитном поле с индукцией B = 15 мТл по окружности радиусом R = 1,4 м. Определите длину волны де Бройля для протона.

42. Определите, какую ускоряющую разность потенциалов должен пройти протон, чтобы длина волны де Бройля λ для него была равна 1 нм.
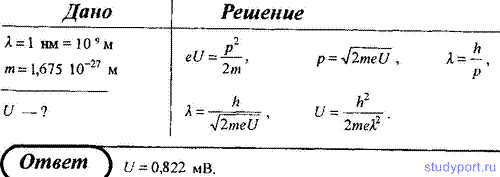
43. Заряженная частица, ускоренная разностью потенциалов U = 500 В, имеет длину волны де Бройля λ = 1,282 пм. Принимая заряд этой частицы равным заряду электрона, определите ее массу.

44. Выведите зависимость между длиной волны де Бройля λ релятивистской частицы и ее кинетической энергией.
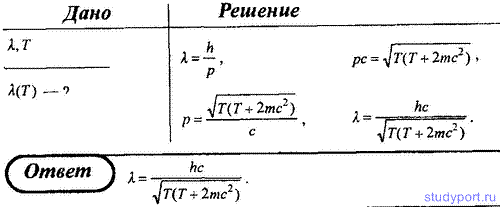
45. Выведите зависимость между длиной волны де Бройля λ релятивистского электрона и ускоряющим потенциалом U.

46. Кинетическая энергия электрона равна 1 кэВ. Определите длину волны де Бройля.

47. Кинетическая энергия электрона равна 0,6 МэВ. Определите длину волны де Бройля.

48. Определите, при каком числовом значении скорости длина волны де Бройля для электрона равна его комптоновской длине волны.

49. Определите, при каком числовом значении кинетической энергии T длина волны де Бройля электрона равна его комптоновской длине волны.

50. Выведите связь между длиной круговой электронной орбиты и длиной волны де Бройля.

51. Определите, как изменится длина волны де Бройля электрона в атоме водорода при переходе его с четвертой боровской орбиты на вторую.

52. В опыте Дэвиссона и Джермера, обнаруживших дифракционную картину при отражении пучка электронов от естественной дифракционной решетки — монокристалла никеля, оказалось, что в направлении, составляющем угол α = 55° с направлением падающих электронов, наблюдается максимум отражения четвертого порядка при кинетической энергии электронов T = 180 эВ. Определите расстояние между кристаллографическими плоскостями никеля.

53. Моноэнергетический пучок нейтронов, получаемый в результате ядерной реакции, падает на кристалл с периодом d = 0,15 нм. Определите скорость нейтронов, если брэгговское отражение первого порядка наблюдается, когда угол скольжения ν = 30° .

54. Параллельный пучок моноэнергетических электронов направлен нормально на узкую щель шириной a = 1 мкм. Определите скорость этих электронов, если на экране, отстоящем на расстоянии l = 20 см от щели, ширина центрального дифракционного максимума составляет Δx = 48 мкм.
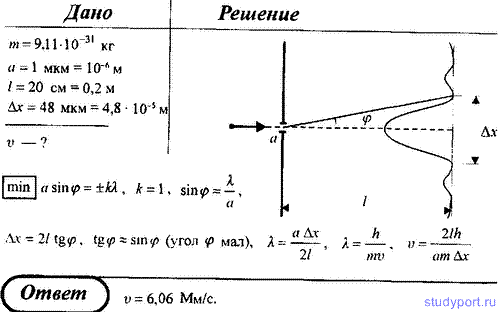
55. Параллельный пучок электронов, ускоренный разностью потенциалов U = 50 В. направлен нормально на две параллельные, лежащие в одной плоскости щели, расстояние d между которыми равно 10 мкм. Определите расстояние между центральным и первым максимумом дифракционной картины на экране, который расположен от щелей на расстоянии l = 0,6 м.
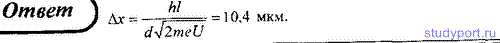
56. Исходя из общей формулы для фазовой скорости ( Vфаз = w/k ), определите фазовую скорость волны де Бройля свободно движущейся с постоянной скоростью v частицы в нерелятивистском и релятивистском случаях.

59. Докажите, что групповая скорость волн де Бройля равна скорости свободно движущейся частицы. Рассмотрите нерелятивистский и релятивистский случаи.

60. Докажите, что для свободно движущейся с постоянной скоростью v частицы выполняется соотношение vфаз u = c2 (u —групповая скорость).

61. Выведите закон дисперсии волн де Бройля, т.е. зависимость фазовой скорости волн де Бройля от их длины волны. Рассмотрите нерелятивистский и релятивистский случаи.

62. Ширина следа электрона (обладающего кинетической энергией T = 1,5 кэВ) на фотопластинке, полученного с помощью камеры Вильсона, составляет Δx = 1 мкм. Определите, можно ли по данному следу обнаружить отклонение в движении электрона от законов классической механики.

63. Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U = 1 кВ. Известно, что неопределенность скорости составляет 0,1% от ее числового значения. Определите неопределенность координаты электрона. Являются ли электроны в данных условиях квантовой или классической частицей?

64. Определите отношение неопределенностей скорости электрона, если его координата установлена с точностью до 10-5 м, и пылинки массой m = 10-12 кг, если ее координата установлена с такой же точностью.

65. Электронный пучок выходит из электронной пушки под действием разности потенциалов U = 200 В. Определите, можно ли одновременно измерить траекторию электрона с точностью до 100 пм (с точностью порядка диаметра атома) и его скорость с точностью до 10%.

66. Электрон движется в атоме водорода по первой боровской орбите. Принимая, что допускаемая неопределенность скорости составляет 10% от ее числового значения, определите неопределенность координаты электрона. Применимо ли в данном случае для электрона понятие траектории?

68. Используя соотношение неопределенностей в форме Δx Δpx >= h , оцените минимально возможную полную энергию электрона в атоме водорода. Примите неопределенность координаты равной радиусу атома. Сравните полученный результат с теорией Бора.

70. Воспользовавшись соотношением неопределенностей, оцените размытость энергетического уровня в атоме водорода: 1) для основного состояния; 2) для возбужденного состояния (время его жизни равно 10-8 с).

71. Длина волны λ излучаемого атомом фотона составляет 0,6 мкм. Принимая время жизни возбужденного состояния Δt = 10 с, определите отношение естественной ширины энергетического уровня, на который был возбужден электрон, к энергии, излученной атомом.

72. Принимая, что электрон находится внутри атома диаметром 0,3 нм, определите (в электрон-вольтах) неопределенность энергии данного электрона.
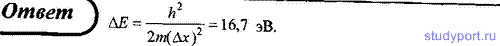
76. Волновая функция, описывающая некоторую частицу, может быть представлена в виде ψ(x, t) = ψ(x)*e –(i/h)*Et . Покажите, что плотность вероятности нахождения частицы определяется только координатной ψ-функцией.

77. ψ-функция некоторой частицы имеет вид ψ = A/r*e-r/a, где r — расстояние этой частицы до силового центра; a — некоторая постоянная. Используя условие нормировки вероятностей, определите нормировочный коэффициент A.
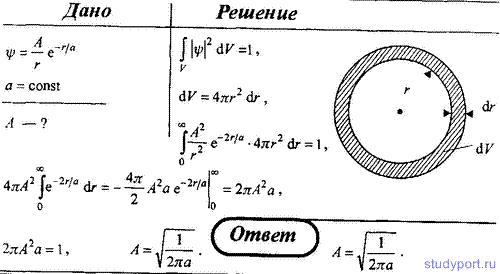
78. Используя условие нормировки вероятностей, определите нормировочный коэффициент А волновой функции ψ = A*е-r/a, описывающей основное состояние электрона в атоме водорода, где r — расстояние электрона от ядра, a — первый боровский радиус.

79. Используя условие нормировки вероятностей, определите нормировочный коэффициент волновой функции ψ(r) = A*e-r^2/(2а^2), описывающей поведение некоторой частицы, где r — расстояние частицы от силового центра; a — некоторая постоянная.

80. Волновая функция ψ = A sin(2πx/l) определена только в области 0 <= x <= l . Используя условие нормировки, определите нормировочный множитель A.

81. ψ-функция некоторой частицы имеет вид ψ = A/r*е-r/a, где r — расстояние этой частицы до силового центра; a — некоторая постоянная. Определите среднее расстояние <r> частицы до силового центра.
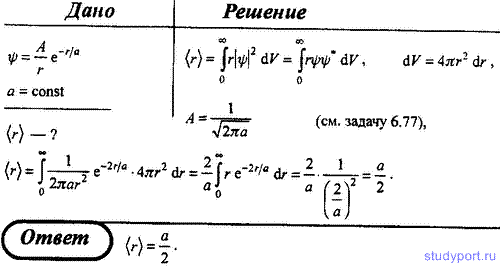
82. Волновая функция, описывающая некоторую частицу, имеет вид ψ = A*e-r^2/(2a^2), где r — расстояние этой частицы до силового центра; a — некоторая постоянная. Определите среднее расстояние <r> частицы до силового центра.

83. Волновая функция, описывающая основное состояние электрона в атоме водорода, имеет вид ψ = A*e-r/a, где r — расстояние электрона от ядра, a — первый боровский радиус. Определите среднее значение квадрата расстояния <r2> электрона до ядра в основном состоянии.

84. Волновая функция, описывающая некоторую частицу, имеет вид ψ(r) = A/r*e-r^2/a^2, где A — нормировочный множитель, равный 1/(корень(πa)*корень(2π)); r — расстояние частицы от силового центра; a — некоторая постоянная. Определите среднее значение квадрата расстояния <r2> частицы до силового центра.

85. Волновая функция, описывающая основное состояние электрона в атоме водорода, имеет вид ψ = A*e-r/a, где r — расстояние электрона от ядра, a — первый боровский радиус. Определите наиболее вероятное расстояние rв электрона до ядра.
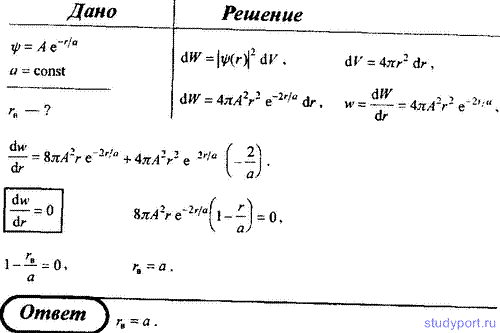
86. Волновая функция, описывающая некоторую частицу, имеет вид ψ = A*e-r^2/(2a^2), где r — расстояние частицы от силового центра; a — некоторая постоянная. Определите наиболее вероятное расстояние rв частицы до силового центра.

92. Запишите уравнение Шредингера для стационарных состояний для свободной частицы, движущейся вдоль оси x, а также определите посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы?
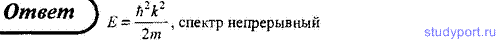
93. Волновая функция, описывающая частицу в момент времени t = 0 , имеет вид ψ(x,0) = A*e-x^2/a^2+ikx, где a и k — некоторые положительные постоянные. Определите: 1) нормировочный коэффициент A; 2) область, в которой частица локализована.
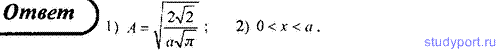
94. Частица находится в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими "стенками". Запишите уравнение Шредингера в пределах "ямы" (0 <= x <= l) и решите его.
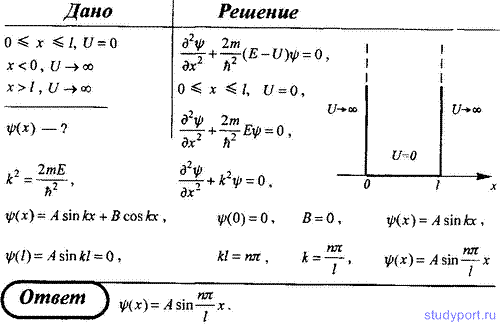
95. Частица находится в одномерной "потенциальной яме" шириной l с бесконечно высокими "стенками". Выведите выражение для собственных значений энергии En.

96. Волновая функция, описывающая состояние частицы в одномерной прямоугольной "потенциальной яме" с бесконечно высокими "стенками", имеет вид ψ(x) = A sin kx . Определите: 1) вид собственной волновой функции ψn(x); 2) коэффициент A , исходя из условия нормировки вероятностей.

97. Известно, что нормированная собственная волновая функция, описывающая состояние электрона в одномерной прямоугольной "потенциальной яме" с бесконечно высокими "стенками", имеет вид ψn(x) = корень(2/l) * sin πnx/l, где l — ширина "ямы". Определите среднее значение координаты <x> электрона.
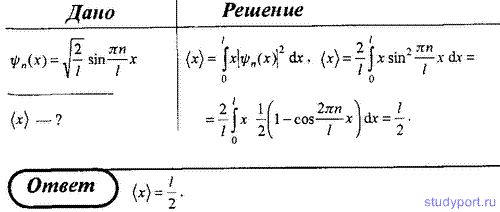
99. Частица в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими "стенками" находится в основном состоянии. Определите вероятность обнаружения частицы в левой трети "ямы".

100. Частица в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими "стенками" находится в возбужденном состоянии (n = 2). Определите вероятность обнаружения частицы в области 3/8*l <= x <= 5/8*l.

101. Электрон находится в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими "стенками". Определите вероятность W обнаружения электрона в средней трети "ямы", если электрон находится в возбужденном состоянии (n = 3). Поясните физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии.
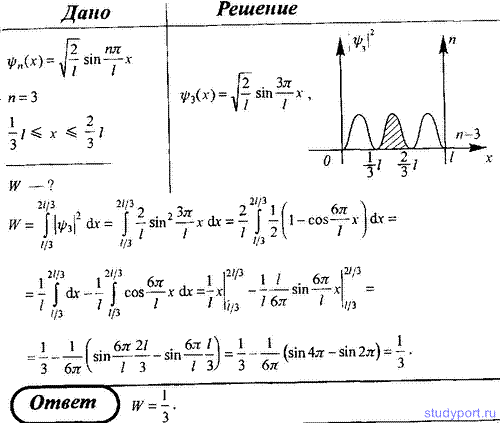
102. Частица в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими "стенками" находится в возбужденном состоянии (n = 3). Определите, в каких точках "ямы" (0 <= х <= l) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните полученный результат графически.

103. Определите, при какой ширине одномерной прямоугольной "потенциальной ямы" с бесконечно высокими "стенками" дискретность энергетического спектра электрона сравнима с его средней кинетической энергией при температуре T.

104. Докажите, что энергия свободных электронов в металле не квантуется. Примите, что ширина l прямоугольной "потенциальной ямы' с бесконечно высокими "стенками" для электрона в металле составляет 10 см.
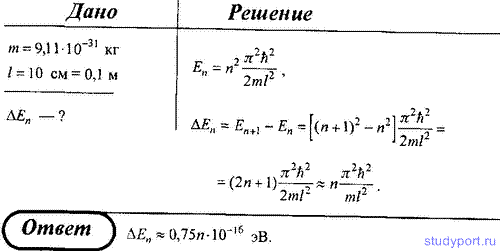
105. Частица находится в одномерной прямоугольной "потенциальной яме" с бесконечно высокими "стенками". Определите, во сколько раз изменяется отношение разности соседних энергетических уровней ΔEn+1,n/En частицы при переходе от n = 3 к n' = 8 . Объясните физическую сущность полученного результата.

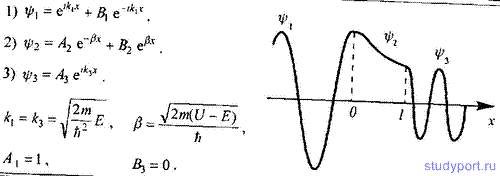
106. Частица с энергией Е движется в положительном направлении оси x и встречает на своем пути прямоугольный потенциальный барьер высотой U и конечной шириной l, причем E < U. Запишите уравнение Шредингера для областей 1, 2 и 3.

107. Для условия задачи 106 запишите решения уравнений Шредингера для областей 1. 2 и 3. ψ-функция обычно нормируется так, что A1= 1. Представьте графически качественный вид ψ-функций.
83. Волновая функция, описывающая основное состояние электрона в атоме водорода, имеет вид ψ = A*e-r/a, где r — расстояние электрона от ядра, a — первый боровский радиус. Определите среднее значение квадрата расстояния <r2> электрона до ядра в основном состоянии.

84. Волновая функция, описывающая некоторую частицу, имеет вид ψ(r) = A/r*e-r^2/a^2, где A — нормировочный множитель, равный 1/(корень(πa)*корень(2π)); r — расстояние частицы от силового центра; a — некоторая постоянная. Определите среднее значение квадрата расстояния <r2> частицы до силового центра.

85. Волновая функция, описывающая основное состояние электрона в атоме водорода, имеет вид ψ = A*e-r/a, где r — расстояние электрона от ядра, a — первый боровский радиус. Определите наиболее вероятное расстояние rв электрона до ядра.
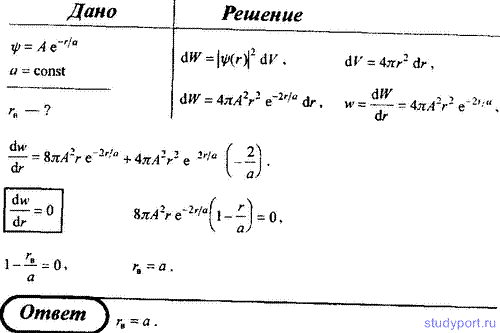
86. Волновая функция, описывающая некоторую частицу, имеет вид ψ = A*e-r^2/(2a^2), где r — расстояние частицы от силового центра; a — некоторая постоянная. Определите наиболее вероятное расстояние rв частицы до силового центра.

92. Запишите уравнение Шредингера для стационарных состояний для свободной частицы, движущейся вдоль оси x, а также определите посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы?
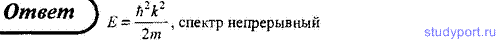
93. Волновая функция, описывающая частицу в момент времени t = 0 , имеет вид ψ(x,0) = A*e-x^2/a^2+ikx, где a и k — некоторые положительные постоянные. Определите: 1) нормировочный коэффициент A; 2) область, в которой частица локализована.
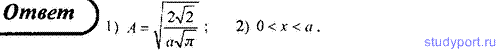
94. Частица находится в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими "стенками". Запишите уравнение Шредингера в пределах "ямы" (0 <= x <= l) и решите его.

95. Частица находится в одномерной "потенциальной яме" шириной l с бесконечно высокими "стенками". Выведите выражение для собственных значений энергии En.

96. Волновая функция, описывающая состояние частицы в одномерной прямоугольной "потенциальной яме" с бесконечно высокими "стенками", имеет вид ψ(x) = A sin kx . Определите: 1) вид собственной волновой функции ψn(x); 2) коэффициент A , исходя из условия нормировки вероятностей.

97. Известно, что нормированная собственная волновая функция, описывающая состояние электрона в одномерной прямоугольной "потенциальной яме" с бесконечно высокими "стенками", имеет вид ψn(x) = корень(2/l) * sin πnx/l, где l — ширина "ямы". Определите среднее значение координаты <x> электрона.
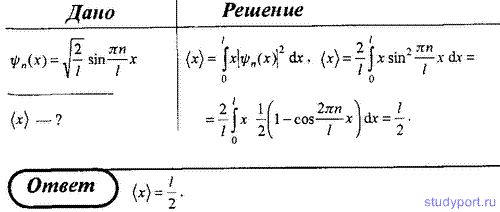
99. Частица в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими "стенками" находится в основном состоянии. Определите вероятность обнаружения частицы в левой трети "ямы".

100. Частица в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими "стенками" находится в возбужденном состоянии (n = 2). Определите вероятность обнаружения частицы в области 3/8*l <= x <= 5/8*l.

101. Электрон находится в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими "стенками". Определите вероятность W обнаружения электрона в средней трети "ямы", если электрон находится в возбужденном состоянии (n = 3). Поясните физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии.

102. Частица в одномерной прямоугольной "потенциальной яме" шириной l с бесконечно высокими "стенками" находится в возбужденном состоянии (n = 3). Определите, в каких точках "ямы" (0 <= х <= l) плотность вероятности обнаружения частицы: 1) максимальна; 2) минимальна. Поясните полученный результат графически.

103. Определите, при какой ширине одномерной прямоугольной "потенциальной ямы" с бесконечно высокими "стенками" дискретность энергетического спектра электрона сравнима с его средней кинетической энергией при температуре T.

104. Докажите, что энергия свободных электронов в металле не квантуется. Примите, что ширина l прямоугольной "потенциальной ямы' с бесконечно высокими "стенками" для электрона в металле составляет 10 см.
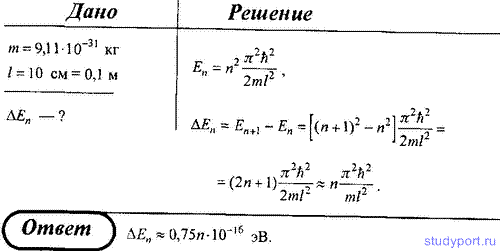
105. Частица находится в одномерной прямоугольной "потенциальной яме" с бесконечно высокими "стенками". Определите, во сколько раз изменяется отношение разности соседних энергетических уровней ΔEn+1,n/En частицы при переходе от n = 3 к n' = 8 . Объясните физическую сущность полученного результата.

106. Частица с энергией Е движется в положительном направлении оси x и встречает на своем пути прямоугольный потенциальный барьер высотой U и конечной шириной l, причем E < U. Запишите уравнение Шредингера для областей 1, 2 и 3.

107. Для условия задачи 106 запишите решения уравнений Шредингера для областей 1. 2 и 3. ψ-функция обычно нормируется так, что A1= 1. Представьте графически качественный вид ψ-функций.

| А) Можно ли представить волну Д‘Бройля как волновой пакет? Б) Как при этом будут связаны групповая скорость волнового пакета u и скорость частицы v? Ответ: 2. а) нет; б) u=v. В бесконечно глубокой потенциальной яме шириной L находится электрон. Вычислить вероятность w нахождения электрона на первом энергетическом уровне в интервале (А, В): (pic). Ответ: 3. w = 2/L. Верны ли следующие утверждения: а) волны Д’Бройля являются монохроматическими. в) групповая скорость фотона равна скорости самого фотона. с) групповая скорость волн Д’Бройля больше скорости частицы. Ответ: 4. а) нет; в) да; с) нет. Верны ли следующие утверждения: а) фазовая скорость волн Д’Бройля больше скорости света в вакууме. в) волны Д’Бройля не испытывают дисперсию. с) волны Д’Бройля не могут быть волновым пакетом. Ответ: 3. а) да; в) нет; с) да. В излучении звезды обнаружен водородоподобный спектр, длины волн которого в 9 раз меньше, чем у атомарного водорода. Определить элемент, которому принадлежит данный спектр. 2. литий В результате поглощения фотона электрон в атоме водорода перешел с первой боровской орбиты на вторую. Чему равна частота этого фотона? 1. 2.5*10^15 Гц Волновые свойства частицы необходимо учитывать, если… ее длина волны де Бройля сравнима с линейными размерами области движения частиц Волновые свойства частицы необходимо учитывать, если ее длина волны де Бройля…. сравнима с линейными размерами области движения частицы Волновые свойства частицы можно не учитывать, если линейные размеры области ее движения… 1. много больше длины волны де Бройля для нее Волновые свойства частицы необходимо учитывать, если ее длина волны де Бройля…. 1.сравнима с линейными размерами области движения частицы Волновые свойства частиц необходимо учитывать, если… 1… ее длина волны де Бройля сравнима с линейными размерами области движения частиц. Волновые свойства частицы можно не учитывать, если линейные размеры области ее движения… 1…много больше длины волны де Бройля для нее Волновая функция, описывающая основное состояние электрона в атоме водорода, имеет вид Ψ = A*exp(r/a), где r – расстояние электрона от ядра a – первый боровский радиус Определите наиболее вероятное расстояние rв электрона до ядра 2. rв = a Волновая функция y(x)=Asin (2px/l) определена только в области 0£ x£ l. Используя условие нормировки, определите нормировочный множитель. 3. A=sqrt(2/l) Во сколько раз энергия частицы, находящейся в «потенциальной яме» с бесконечно высокими «стенками» в состоянии с n=4 отличается от энергии частицы с состоянием n=2? 3. больше в 4 раза; Воспользовавшись соотношением неопределенностей оценить ширину энергетического уровня водорода : 1) для основного состояния; 2) для возбужденного состояния ( время его жизни 10-8) 1. 1)0; 2)4,14 нэВ Выберите верные утверждения в) волны де Бройля не могут быть ни монохроматическими, ни представлять из себя волновой пакет; г) групповая скорость любого волнового пакета и скорость частицы, обладающей свойствами волны, совпадают 4. в, г Выберите верное утверждение 5. корпускулярно-волновой дуализм присущ всем формам материи Выберите НЕВЕРНОЕ утверждение: г. При n = 1 атом может находиться лишь очень малое количество времени.( Δt -> 0) n = 1 – первый энергетический уровень Выберите неверное утверждение 1. В бесконечно глубокой потенциальной яме энергия частицы изменяется непрерывно Вывести связь между радиусом круговой электронной орбиты r и длиной волны де Бройля l, где n – номер стационарной орбиты. 2pr=nl Вывести зависимость между длиной волны де Бройля l релятивистской частицы и ее кинетической энергией. 2. Lam=hc/sqrt(T(T+2mo*c^2)) Вывести зависимость между длиной волны де Бройля l релятивистского электрона и ускоряющим потенциалом U. 4. lam= hc/ sqrt(eU(2mo*c^2 + eU)) Какую наименьшую энергию надо сообщить иону He+, находящемуся в основном состоянии, чтобы он смог испустить фотон, занимающий в спектре гелия то же место, что и головная линия серии Бальмера в спектре водорода (энергия связи атома водорода в основном состоянии E0=13,6 эВ)? 2. Eмин=48,4 эВ Коэффициент позрачности D потенциального барьера - … отношение плотности потока прошедших частиц к плотности потока падающих | Вычислить теоретическую величину разрешающей способности а, которую следует ожидать от электронного микроскопа с ускоряющим напряжением 100 кВ при значении числовой апертуры g=0,1 (a » 0,6l / g) 2. 0.24 Å Вычислите дебройлевскую длину волны мяча массой 0,2 кг, летящего со скоростью 15 м/с. 2. 2,2∙10-34 м Вычислить среднее время жизни возбужденных атомов, если известно, что интенсивность спектральной линии, обусловленной переходом в основное состояние, убывает в n = 25 раз на расстоянии l = 2,5 мм вдоль пучка атомов, скорость которых v = 600 м/с. 4. τ = 1,3 мкс Вычислить для атома водорода радиус второй боровской орбиты и скорость электрона на ней 2. r2=2,12∙10-10 м, V2=1,09∙106 м/с Длина волны излучаемого атомом фотона равна 0,6 мкм. Принимая время жизни возбужденного состояния Δt = 10-8 c, определите отношение естественной ширины энергетического уровня ΔE к энергии, излученной атомом. E. ΔE/E? 4. 2 10-7 Длина волны резонансной линии ртути λ = 253,65 нм. Среднее время жизни атомов ртути в состоянии резонансного возбуждения τ = 0,15 мкс. Оценить отношение доплеровского уширения этой линии к ее естественной ширине при Т = 300 К, если , где M – молярная масса. 4. Δλ доп / Δλ ест ≈ 10 ³ Длина волны де Бройля для частицы определяется по формуле λв=… где p – импульс частицы, с- скорость света, v – частота. 2.h/p. Длина волны де Бройля электрона равна 1,26 пм. Определить кинетическую энергию электрона. 2. Т = 0,55 МэВ Длина волны излучаемого атомом фотона сотавляет 0,7 мкм. Принимая время жизни возбужденного состояния, определите отношение естественной ширины энергетического уровня, на котором был возбужден электрон, к энергии, излученной атомом.(2с) 4. 2.33*10-7м Если u – групповая скорость дебройлевских волн, v – скорость свободной частицы,vфаз – фазовая скорость волн де Бройля свободной частицы, то: 2. u=v ; vфаз=v/2 Закончите определение:Туннельный эффект-это явление, при котором квантовая частица проходит через потенциальный барьер при 1. E < Uо Заряженная частица, ускоренная разностью потенциалов U = 500 В имеет длину волны де Бройля λ = 1,282 пм. Принимая заряд этой частицы равным заряду электрона, определите ее массу. 4. m = 1,67•10-27 кг Заряженная частица, ускоренная разностью потенциалов U=500 В, имеет длину волны де Бройля l=1,282 пм. Принимая заряд этой частицы равным заряду электрона, определить соотношение ее массы m с массой электрона me. 4. m=1837me Заряженная частица, ускоренная разностью потенциалов U, имеет длину волны де Бройля l. Принимая заряд этой частицы равным заряду электрона е, определить ее массу m. 2. m=h^2/2e*Lam^2*U Исходя из формулы dn= sqrt(2m^3*E)/pi^2h^3 dE, найти функцию распределения свободных электронов в металле при T=0 по дебройлевским длинам волн. 3.dn=8pi*Lam^-4*dLam Исходя из соотношения неопределенностей dx*dp>=h , оцените размер атома водорорда в состоянии с минимальной энергией. (2с) 3. Rmin=4pi*eps0*h^2/ml^2 Исходя из соотношения неопределённостей оценить минимальную кинетическую энергию электрона, движущегося по стационарной орбите атома водорода 4. 4эВ; Используя теорию Бора для водорода, определить скорость движения электрона в возбужденном состоянии при n=2. 2.0,55 Мм/с Используя теорию Бора, определить орбитальный магнитный момент электрона, движущегося по третьей орбите атома водорода 2.pm=2,8∙10-23 A∙м2 Используя теорию Бора для атома водорода, определите радиус ближайшей к ядру орбиты (первый Боровский радиус). 4. 53 пм Имеются 2 электрона. Кинетическая энергия одного из них равна 9 КэВ. Отношение соответствующих им длин волн де Бройля (первой ко второй) равно 1,73. Найти кинетическую энергию второго электрона. 3. 3 КэВ Как соотносятся между собой коэффициенты прозрачности следующих потенциальных барьеров: а) барьер ширины L для частицы массой 4m (D1) б) барьер ширины 2L для частицы массой m (D2): 2. D1 = D2 Какую максимальную скорость должны иметь электроны, чтобы перевести ударом атом водорода из первого состояния в третье? 3.Vmin=2,06 Мм/c Какой наименьшей скоростью v должен обладать электрон для того, чтобы ионизовать ион Не+ ? Потенциал ионизации атома водорода U=13,5 В. 5. 4,4•106 м/с Квантовая частица находится в основном состоянии (n=1) в одномерном потенциальном ящике шириной l с абсолютно непроницаемыми стенками (0≤x≤l). Сравнить вероятность пребывания частицы в областях a) 0≤x≤l/2 и b) l/2≤x≤l. 1.a=b Найти наибольшую длину волны видимой области спектра излучения атома водорода. 3.λmax=6,56∙10-7м | На прямоугольную потенциальную ступеньку беcконечной протяженности и высотой, равной 2 эВ, налетает электрон с энергией3 эВ. Чему равен коэффициент надбарьерного отражения? 2. R=(sqrt3 – 1 / sqrt3 + 1)^2 Найти квантовое число п, соответствующее возбужденному состоянию иона Не+, если при переходе в основное состояние этот ион испустил последовательно два фотона с длинами волн 108,5 и 30,4 нм (постоянная Ридберга R=1,097×107 м-1 ). 5. n=5 На какую орбиту с основной перейдет электрон в атоме водорода при поглощении фотона с энергией 1,93×10-18 Дж? O: 3. Найти для атомов легкого и тяжелого водорода (Н и D) разность длин волн головных линий серии Лаймана (справка: постоянная Ридберга R=1,097×107 м-1, масса электрона me=0,511 МэВ, масса протона mp=937,86 МэВ, масса дейтрона mD=1876,13 МэВ). 3. lH-lD=33 пм Определите длину волны фотона, испускаемого при переходе электрона в одномерной прямоугольной “потенциальной яме” с бесконечно высокими “стенками” шириной 1 из состояния n = 2 в состояние с наименьшей энергией. 1. Lam= 8cml^2/ 3h Определите, при каком числовом значении кинетической энергии Т длина волны де Бройля электрона равна его комптоновской длине волны. 3.T = 3,36•10-14 Дж Определите связь между групповой и фазовой скоростями волны де Бройля 1.u=vф-ldvф /dl Определите длину волны де Бройля l для электрона, обладающего кинетической энергией Т = 60 эВ. (h = 6.62*10-34 Джс, m0 (масса покоя электрона) – 9.11*10-31 кг 1.158 пМ. Определите число спектральных линий, испускаемых атомарным водородом, возбуждённым на n-й энергетический уровень. 1. N = n*(n-1)/2 Определите, какие спектральные линии появятся в видимой области спектра излучения атомарного водорода под действием ультрафиолетового излучения с длиной волны λ= 95 нм (рис) 4. все ответы верны. Определите частоту света, излучаемого атомом водорода, при переходе электрона на уровень с главным числом n=2, если радиус орбиты электрона изменился в k=9 раз. 4. ν = 0,731∙1015 Гц Определите, на сколько изменилась энергия электрона в атоме водорода при излучении атомом фотона с длиной волны λ. 3. dE=hc/lam Определите энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй. 2.1,9 эВ Определите минимальную энергию фотона в видимой серии спектра водорода (серии Бальмера) 2. 1,9 эВ Определите максимальную энергию фотона в серии Бальмера спектра водорода. 4. 3,4 эВ Определите отношение неопределенностей скорости электрона, если его координата установлена с точностью до 10-5 м, и пылинки массой m=10-12 кг, если ее координата установлена с такой же точностью. 1. 1,1∙1018 Определите отношение неопределенностей скорости электрона и пылинки массой m=1.3*1014кг, если их координаты установлены с точностью 10-4 м. 2. 1.43*1016 Определите отношение неопределённостей скорости электрона и пылинки массой m=10-12 кг, если их координаты установлены с точностью до 10-5 м 3. ∆Ve/∆Vп = 1,1∙1018 Определите массу пылинки, если отношение неопределенностей скорости электрона и пылинки равно 1,1∙1018 .Координаты электрона и пылинки установлены с точностью до 10-5 м. 3. m=10-12 кг Определите: а) возможные значения квантового числа j ; б) возможные значения (в единицах ћ) полного момента импульса Lj 3f-электрона. 3. а) 7/2 или 5/2; б) 3 ћ√7/2 или ћ√35/2 Определите энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй 2. 1.89 эВ Определите длину волны света, излучаемого возбужденным атомом водорода, при переходе электрона на вторую орбиту, если радиус орбиты электрона уменьшился в 4 раза 1. 485нм Определите длину волны де Бройля l для электрона, обладающего кинетической энергией Т = 60 эВ.(h = 6.62•10-34 Дж×с, m0 = 9.11•10-31 кг.) 1. 158 пм Определите частоту f вращения электрона по третьей орбите атома водорода в теории Бора. 1. f = 2,43∙1014 Гц Определите длину волны спектральной линии, соответствующей переходу электрона в атоме водорода с шестой боровской орбиты на вторую(рис). К какой серии относится эта линия и какая она посчёту? О:1 Определите энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй. 1. Е3,2 = 1,89 эВ Определите скорость υ электрона на третьей боровской орбите атома водорода 1. υ3 = 0,731 Мм/с |
| Определите длину волны спектральной линии, излучаемой при переходе электрона с более высокого уровня энергии на более низкий, если при этом энергия атома уменьшилась на ΔE = 10эВ (1эВ=1,6 * 10-19 Дж) 2. 124 нм Определить максимальную и минимальную энергии фотона в видимой серии спектра водорода (серии Бальмера). 3. Emin=5/36hR, Emax=1/4hR Определить период Т обращения электрона, находящегося в атоме водорода в стационарном состоянии. 3. 0,15 *10^-15с Определить с помощью соотношения неопределённостей эффективное расстояние электрона от ядра атома водорода. 3. rэфф = ħ2/me2 Определить скорость электрона в возбужденном атоме водорода при n=3. 1/3* e^2/4pi eh Определить w-круговую частоту обращения электрона на n-й круговой боровской орбите водородоподобного иона. W= mk^2*e^4*Z^2/h^3n^3 Определить для иона Не+ потенциал ионизации. Постоянная Ридберга R=2,07×1016 с-1; постоянная Планка =1,0546×10-34 Дж×с; элементарный заряд e=1,6021892•10-19 Кл. 1. 54,5 В Определить иона Не+ первый потенциал возбуждения. Постоянная Ридберга R=2,07×1016 с-1; постоянная Планка =0,659×10-15 эВ×с 1. 40,8 В Определить скорость v электрона на третьей орбите атома водорода. 2. v = e2/(12pe0ħ) Определить частоту f вращения электрона, находящегося на первой боровской орбите. O: f=m*e^2 / 32eps^2*h^3 Определить длину волны де Бройля для электрона, находящегося в атоме водорода на третьей боровской орбите. Первый боровский радиус a0=5,28×10–11 м. 3. 1нм Определить значение орбитального момента импульса PQ электрона в возбужденном атоме водорода при максимальном орбитальном квантовом числе l, если энергия возбуждения E = -12.9 эВ 2. 2.6*10^-34 Определить минимально вероятную энергию Е для квантовой частицы, находящейся в бесконечно глубокой потенциальной яме шириной а: 4. E = h2/8ma2 Определить для иона Не+ энергию связи электрона в основном состоянии. Постоянная Ридберга R=2,07×1016 с-1; постоянная Планка =1,0546×10-34 Дж×с; элементарный заряд e=1,6021892•10-19 Кл.4.54,5 эВ Определить первый потенциал возбуждения атома водорода, где R – постоянная Ридберга, h – постоянная Планка, е –элементарный заряд. 2.j1=3Rhс/(4e) Определить минимальную скорость электрона, необходимую для ионизации атома водорода, если потенциал ионизации атома водорода Ui = 13,6В 4. 2•106 м/с Определить орбитальный момент импульса Pq электрона с максимальным квантовым числом, если энергия возбуждения ∆F=12,09. 1. 2,6 ∙ 10-34 Дж∙с Определить длину волны де Бройля для нейтрона, движущегося со средней квадратичной скоростью при T=290 К. Постоянная Планка h=6,63×10–34 Дж×с, масса нейтрона m=1,675×10–27 кг, постоянная Больцмана k=1,38×10–23 Дж/К. 1. 148 пм Определить, какую ускоряющую разность потенциалов должен пройти протон, чтобы длина волны де Бройля была равна l. 4. U=h^2/ 2meLam^2 Определить дебройлевскую длину волны движущегося электрона, если известно, что масса его на 1% больше массы покоя. 3.0.173 Å Определить длину волны де Бройля l, характеризующую волновые свойства электрона, если его скорость v = 1 Мм/с. 2. 727 пм Определить длину волны де Бройля l электрона, если его кинетическая энергия Т = 1кэВ 3. 39 пМ Определить длину волны де Бройля l для нейтрона, движущегося со средней квадратичной скоростью при температуре Т=290 К 3. 148 пм Определить, какую ускоряющую разность потенциалов должен пройти протон, чтобы длина волны де Бройля l для него была равна 1 нм. 1.U=0,822 мВ Определить, при каком числовом значении скорости длина волны де Бройля для электрона равна его комптоновской длине волны. 4.v=2,12 м/с Определить длину волны де Бройля l, характеризующую волновые свойства электрона, если его скорость v = 1 мм/с. ( ) 2. 0,727 м Определить длину волны де Бройля для нейтрона, движущегося со средней квадратичной скоростью при Т=290К. 2. 148 пм Определить длину волны де Бройля l электрона, если его кинетическая энергия Т = 500 эВ 3.54 пм Определить длину волны l, соответствующую второй спектральной линии в серии Пашена. Постоянная Ридберга R=1,1×107 м–1. 1. 1,28 мкм | Определить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй. Постоянная Ридберга R=2,07×1016 c–1, постоянная Планка ħ=0,659×10–15 эВ×с. 1. 1,89 эВ Определить минимальную энергию фотона в видимой серии спектра водорода (серии Бальмера). Постоянная Ридберга R=2,07×1016 c–1, постоянная Планка ħ=0,659×10–15 эВ×с. 2. 1,89 эВ Определить максимальную энергию фотона в видимой серии спектра водорода (серии Бальмера). Постоянная Ридберга R=2,07×1016 c–1, постоянная Планка ħ=0,659×10–15 эВ×с. 3. 3,41 эВ Определить длину волны спектральной линии, соответствующую переходу электрона в атоме водорода с шестой боровской орбиты на вторую. Постоянная Ридберга R=1,1×107 м–1. 3. 0,41 мкм Определить длину волны l спектральной линии, излучаемой при переходе электрона с более высокого уровня энергии на более низкий уровень, если при этом энергия атома уменьшилась на DE=10 эВ. Постоянная Планка h=4,14×10–15 эВ×с. 3. 124 нм Определить частоту света, излучаемого атомом водорода, при переходе электрона на уровень с главным квантовым числом n, если радиус орбиты электрона изменился в k раз, R – постоянная Ридберга. 2.v=R(1-1/k)/n^2 Определить потенциал ионизации атома водорода. Постоянная Ридберга R=2,07×1016 c–1, постоянная Планка ħ=0,659×10–15 эВ×с. 3.13,6 В Определить квантовое число n возбужденного состояния атома водорода, если известно, что при переходе в основное состояние атом излучил фотон с длиной волны l = 97,25 нм O: 4. Определить квантовое число n возбужденного состояния атома водорода, если известно, что при переходе в основное состояние атом излучил два фотона, с l1 = 656,3 нм и l2 = 121,6 нм. O: 3 Общее уравнение Шредингера имеет вид: Какие условия накладываются на волновую функцию частицы? 4. а,в,г а) волновая функция должна быть конечной в) волновая функция должна быть однозначной г) волновая функция должна быть интегрируемой Основываясь на том, что энергия ионизации атома водорода равна Ei=13,6 эВ, определить первый потенциал возбуждения j1 этого атома. 2. 10,2 В Основываясь на том, что энергия ионизации атома водорода Ei=13,6 эВ, определить в электрон-вольтах энергию фотона, соответствующую самой длинноволновой линии серии Бальмера. 1. 1,89 эВ Основываясь на том, что первый потенциал возбуждения атома водорода j1=10,2 В, определить в электрон-вольтах энергию фотона, соответствующую второй линии серии Бальмера. 3. 2,55 эВ Отношение комптоновской длины волны к длине волны де Бройля для частицы равно 3∙10-4. Найти скорость, с которой движется частица. 1. 9∙104 м/с Оценить минимальную дебройлевскую длину волны свободных электронов в металле при T=0, полагая, что металл содержит по одному свободному электрону на атом, а его решетка является простой кубической с периодом а. 3. Lam=2a Оценить неопределенность скорости электрона в атоме водорода, полагая размератома водорода Dx = 0,10 нм 1. 1,16×106 м/с Параллельный пучок электронов падает нормально на диафрагму с узкой прямоугольной щелью шириной a = 2 мкм. Определить положение 2-го дифракционного минимума на экране, отстающем от щели на расстояние l = 50 см. Скорость всех электронов одинакова и равна 4.5*10^6 m/c 3. 8*10^-5m Параллельный пучок электронов падает нормально на диафрагму с узкой прямоугольной щелью шириной a = 2 мкм. Во сколько раз отличается ширина 1-го дифракционного максимума b1 от центрального дифракционного максимума b? Скорость всех электронов одинакова и равна 4.5*10^6 m/c 3. 0,5 При какой температуре T атомы ртути имеют кинетическую энергию поступательного движения, достаточную для ионизации? Потенциал ионизации атома ртути U = 10,4 В. Молярная масса ртути M=200,5 г/моль; универсальная газовая постоянная R=8,31 Дж/(моль×К). 5. 8•104 К При каком значении кинетической энергии дебройлевская длина волны электрона равна его комптоновской длине волны. 2. 0.21 МэВ Протон и электрон, обладая одинаковой энергией, движутся в положительном направлении оси Х и встречают на своем пути прямоугольный потенциальный барьер. Определите во сколько раз надо сузить потенциальный барьер, чтобы вероятность прохождения его протоном была такая же, как для электрона. 2. sqrt(mp/mв) Пучок электронов встречает на своём пути потенциальный барьер (U<E). Определить отношение волн де Бройля перед и за барьером, если коэффициент отражения R=1/9 3. 1/2 Свободная частица движется со скоростью 10 м/с. Определить отношение фазовой и групповой скоростей волн де Бройля. 3. 9∙1014 | Прямоугольный потенциальный барьер имеет ширину 0,3 нм. Определить разность энергий Uo-E, при которой вероятность прохождения электрона сквозь барьер составляет 0,8 ( |
| Частица находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Найти квантовое число n энергетического уровня частицы, если интервалы энергии до соседних с ним уровней (верхнего и нижнего) относятся как h:1, где h=1.4 2. 3 Частица находится в возбужденном (n = 4) состоянии в одномерном потенциальном ящике шириной l с абсолютно непроницаемыми стенками. В какой из областей A(0 <= x <= l/3) и B(2/3 <= x <= l) вероятность пребывания электрона больше 3.A=B Чему будет равен коэффициент прозрачности потенциального барьера D, если увеличить его ширину в два раза? 3. D²; Что произойдет с фазовой скоростью волн де Бройля при уменьшении скорости частицы? 2.увеличится Что определяет плотность вероятности обнаружить частицу в некотором месте пространства ? 3. 1,3,4 1) Форму электронных облаков. 3) Анизотропные свойства кристалла. 4) Химические связи внутри кристалла. Электрон находится внутри атома диаметром 0,3 нм, определите (в эВ) неопределенность энергии данного электрона 2. dE=16.7 эВ Электрон обладает кинетической энергией Т=60эВ. Определите длину волны де Бройля l для электрона 1. 158пм Электрон выбит из атома водорода, находящегося в основном состоянии, фотоном, энергия которого Е = 17,7 эВ. Определите скорость электрона за пределами атома. 1.1,2 Мм/с Электрон выбит из атома водорода, находящегося в основном состоянии, фотоном, энергия которого Е = 20 эВ. Определите скорость электрона за пределами атома. 3. 1,5 Мм/с Электрон в атоме водорода с первой орбиты переходит на орбиту, радиус которой в девять раз больше. Какую энергию должен поглотить атом? 3.11,9 эВ Электрон в атоме водорода переходит с одного энергетического уровня на другой. Какие переходы соответствуют поглощению энергии. 2. 1,2,5 Электрон выбит из атома водорода, находящегося в основном состоянии, фотоном энергии e. Определить скорость v электрона за пределами атома, где Еi – потенциал ионизации. 4. v= sqrt(2(eps-Ei)/m) Электрон наталкивается на потенциальный барьер конечной высоты. При каком значении энергии Е электрона он не пройдет через потенциальный барьер высотой U0: 4. нет верных ответов Электрон находиться в прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы L=0,2 нм, энергия электрона En=37,7эВ. Определить номер энергетического уровня. 2. 2 Электрон в атоме находится в f-состоянии. Определите момент импульса электрона. 4. 3.46 ћ Электрон выбит из атома водорода, находящегося в стационарном состоянии, фотоном, энергия которого ε = 17,7. Определить скорость электрона за пределами атома 1.υ = 1,2 Мм/с Электронный пучок ускоряется в электроннолучевой трубке разностью потенциалов U = 4 кВ. Неопределенность скорости составляет 0,001 от её числового значения. Определить неопределенность координаты электрона. 1. dx=19.4 нм Электронный пучок ускоряется в электронно-лучевой трубке под действием разности потенциалов 800 В. Определить разрешающую способность электрона на мониторе, если неопределенность скорости составляет 0.1%. 4. 43,6 нм Электрон движется в атоме водорода по первой боровской орбите. Принимая, что допускаемая неопределённость скорости составляет 10% от её числового значения, определите неопределённость координаты электрона. 4. ∆х=3,34∙10-9м Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U=1кВ. Известно, что неопределённость скорости составляет 0,1 % от её числового значения. Определите неопределённость координаты электрона 1. ∆x = 38,8нм Энергия связи электрона в основном состоянии атома Не равна E0=24,6 эВ. Найти энергию, необходимую для удаления обоих электронов из этого атома (справка: энергия связи атома водорода в основном состоянии E0’=13,6 эВ). 4.E=79,0 эВ | Чем определяется вид Y - функции волны де Бройля частицы в стационарном уравнении Шредингера? 4. Видом функции потенциальной энергии частицы U |
Дата добавления: 2015-01-29; просмотров: 6713; Мы поможем в написании вашей работы!; Нарушение авторских прав |