Анализ процесса изменения технического состояния гидрофильтра

Объектом управления является гидрофильтр, техническое состояние которого определяется параметром - давление гидрожидкости в фильтре, изменение которого представляет собой монотонную случайную функцию времени t.

Наиболее полным описанием случайной функции является n-мерный закон или n-мерная плотность распределения случайной функции. Зная эту плотность распределнеия, можно достаточно точно решать задачи надежности, диагностики и технической эксплуатации. Однако строгое решение задачи с использованием n-мерных характеристик связано с значительными математичекими трудностями. Наиболее простой характеристикой случайной функции является одномерная плотность распределения , которая характеризует распределение случайной величины 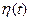в любой произвольный момент времени t. Это означает, что известны плотности распределния в любые фиксированные моменты времени, но одномерная функция распределния не описывает зависимости

между значениями случайной функции в различные моменты времени t. Будем полагать, что реализации случайного процесса изменяются во времени монотонно.

Плотность нормального распределения параметра:

Параметры плотности распределения 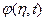определяются в начальные и центральные моменты. Здесь

, - математическое ожидание и среднее квадратическое отклонение параметра в фиксированный момент времени,

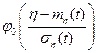- плотность нормированного, центрированного нормального распределения,

- значение параметра в интервале

При t=0 ч

;

;

.

Плотность нормального распределения

При

При .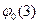

При t=1000 ч.

Плотность нормального распределения

При .

При .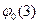

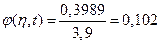При t=2000 ч.

Плотность нормального распределения

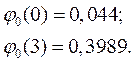
При .

При .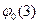

0 1000 2000 t, ч

Рис. 2.1. Одномерная плотность распределения давления

Для оценки и прогнозирования параметра на период 4000 ч. предполагаем, что математическое ожидание и среднее квадратическое отклонение аппроксимированы линейной зависимостью.

,

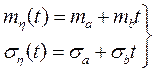где - коэффициенты моментных функций.

Осуществим прогноз значений моментных функций для наработки t=4000 ч.

0 1000 2000 3000 4000 t, ч

Рис. 2.2. Прогноз значений моментных функций