
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Квайна-Мак-Класки.
Разобьем наборы носителя 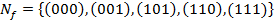 по классам по количеству единиц в наборе и применим операцию склейки ко всем наборам из соседних классов. Наборы, участвующие в склейке, помечаем «∗». Получим следующую таблицу:
по классам по количеству единиц в наборе и применим операцию склейки ко всем наборам из соседних классов. Наборы, участвующие в склейке, помечаем «∗». Получим следующую таблицу:
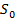
| (000) ∗ | (00−) |

| (001) ∗ | (−01) |
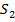
| (101) ∗ (110) ∗ | (1−1) (11−) |

| (111) ∗ |
Найдем простые импликанты, соответствующие непомеченным наборам. Выпишем сокращенную ДНФ.
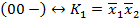

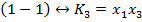
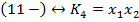
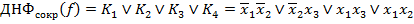
Составим таблицу покрытия. Обведем единственные в столбце метки, простые импликанты, соответствующие таким меткам, являются ядровыми, а их дизъюнкция ядровой ДНФ.
| (000) | (001) | (101) | (110) | (111) | |

| |||||
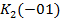
| |||||

| |||||

|

Составим по таблице покрытия вспомогательную функцию Патрика.
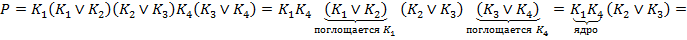
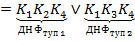
Слагаемому 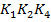 соответствует
соответствует  , а слагаемому
, а слагаемому 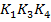
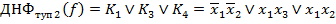 . Обе тупиковые ДНФ являются минимальными для данной функции.
. Обе тупиковые ДНФ являются минимальными для данной функции.
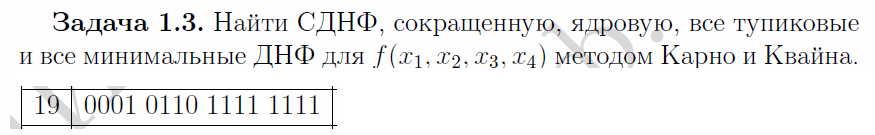
Решение:
1) По вектору значений функции 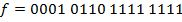 составим карту Карно.
составим карту Карно.
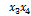
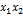
|
| ||||
| 1 |
| ||||
| |||||
| |||||
Максимальный интервал 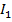 образован двумя соседними строками. Остальные максимальные интервалы состоят из двух вершин, то есть максимальному интервалу
образован двумя соседними строками. Остальные максимальные интервалы состоят из двух вершин, то есть максимальному интервалу 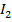 соответствуют вершины
соответствуют вершины 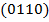 и
и 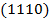 ,
, 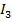 соответствуют вершины
соответствуют вершины 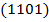 и
и 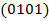 , а
, а  соответствуют вершины
соответствуют вершины 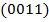 и
и  .
.
2) Выпишем простые импликанты, соответствующие максимальным интервалам.
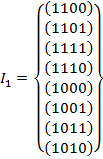
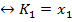

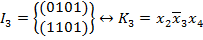
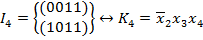
Тогда сокращенная ДНФ есть дизъюнкция всех простых импликантов 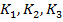 , то есть
, то есть
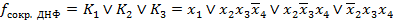 .
.
Отметим звездочкой на карте Карно вершины, покрытые только одним максимальным интервалом. Интервалы, покрывающие такие вершины, и соответствующие им импликанты являются ядровыми, их дизъюнкция — ядровой ДНФ.
 .
.
3) Составим функцию Патрика для заданной функции, перечисляя наборы по строкам карты Карно.
 .
.
Очевидно, что ядровая ДНФ совпадает с сокращенной, тупиковой и минимальной ДНФ.
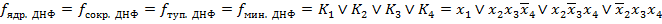 .
.
Дата добавления: 2015-01-29; просмотров: 280; Мы поможем в написании вашей работы!; Нарушение авторских прав |