КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Квайна-Мак-Класки. Выпишем носитель функции по карте Карно (предыдущий метод минимизации).
Выпишем носитель функции 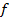 по карте Карно (предыдущий метод минимизации).
по карте Карно (предыдущий метод минимизации).
 .
.
Разобьем наборы носителя 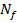 по классам по количеству единиц в наборе и применим операцию склейки ко всем наборам из соседних классов. Наборы, участвующие в склейке, помечаем «∗». Получим следующую таблицу:
по классам по количеству единиц в наборе и применим операцию склейки ко всем наборам из соседних классов. Наборы, участвующие в склейке, помечаем «∗». Получим следующую таблицу:
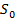
| ||||

| (1000) * | (1−00)* (100−)* (10−0)* | (1−0−)* (1−−0)* (1−0−) — дубль (10−−)* (1−−0) — дубль (10−−) — дубль | (1−−−) (1−−−) — дубль (1−−−) — дубль |
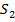
| (0011)* (0101)* (0110)* (1100)* (1001)* (1010)* | (−011) (−101) (−110) (110−)* (11−0)* (1−01)* (10−1)* (1−10)* (101−)* | (11−−)* (11−−) — дубль (1−−1)* (1−−1) — дубль (1−1−)* (1−1−) — дубль | |

| (1101)* (1110)* (1011)* | (11−1)* (111−)* (1−11)* | ||

| (1111)* |
Найдем простые импликанты, соответствующие непомеченным наборам (дубли не учитываем). Выпишем сокращенную ДНФ.

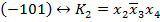



Составим таблицу покрытия. Обведем единственные в столбце метки, простые импликанты, соответствующие таким меткам, являются ядровыми, а их дизъюнкция ядровой ДНФ.
| (0011) | (0101) | (0110) | (1100) | (1101) | (1111) | (1110) | (1000) | (1001) | (1011) | (1010) | |

| |||||||||||

| |||||||||||

| |||||||||||

|
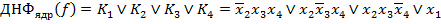 .
.
Составим по таблице покрытия вспомогательную функцию Патрика.
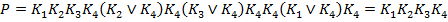 . Получаем, что ядровая ДНФ совпадает с сокращенной, тупиковой и минимальной ДНФ.
. Получаем, что ядровая ДНФ совпадает с сокращенной, тупиковой и минимальной ДНФ.
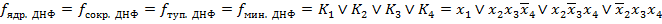 .
.

Решение:
1) По вектору значений функции  составим карту Карно.
составим карту Карно.
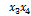
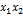
|
| |||||
|
| |||||
|
| |||||
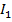
|
Отметим на карте максимальные интервалы. Максимальный интервал 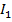 образуют 4 двоичных набора, стоящие в крайней строке, то есть
образуют 4 двоичных набора, стоящие в крайней строке, то есть  . Еще 6 пар рядом стоящих вершин с номерами
. Еще 6 пар рядом стоящих вершин с номерами 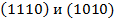 ,
,  ,
,  ,
, 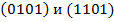 ,
,  ,
,  соответственно также образуют максимальные интервалы.
соответственно также образуют максимальные интервалы.
2) Найдем простые импликанты, соответствующие максимальным интервалам.







Тогда сокращенная ДНФ есть дизъюнкция всех простых импликантов  , то есть
, то есть
 .
.
Отметим звездочкой на карте Карно вершины, покрытые только одним максимальным интервалом. Интервалы, покрывающие такие вершины, и соответствующие им импликанты являются ядровыми, их дизъюнкция — ядровой ДНФ. На карте Карно есть только две вершины 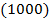 и (
и (  , покрытые ровно одним максимальным интервалом
, покрытые ровно одним максимальным интервалом 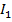 .
.
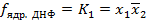 .
.
3) Составим функцию Патрика для заданной функции, перечисляя наборы по строкам карты Карно.
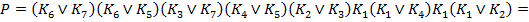

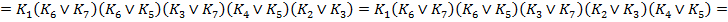



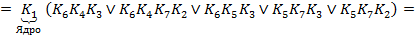
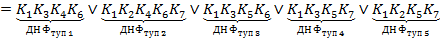
4) Выпишем все тупиковые ДНФ и найдем их ранг. Среди всех тупиковых ДНФ укажем минимальную ДНФ заданной функции.
 ,
,  ;
;
 ,
,  ;
;
 ,
, 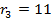 ;
;
 ,
, 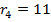 ;
;
 ,
,  .
.
Дата добавления: 2015-01-29; просмотров: 532; Мы поможем в написании вашей работы!; Нарушение авторских прав |