
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Поле корреляции и подходящая линия регрессии
5. Измерение степени тесноты связи и оценка ее существенности используют:
– Линейный коэффициент корреляции – применяют для парной линейной зависимости между двумя количественными признаками:
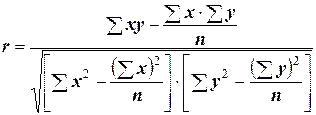
Его пределы [–1; +1]; чем ближе к 1 по абсолютной величине, тем связь теснее. Знак коэффициента показывает направление связи («+» – прямая связь, «–» – обратная).при равенстве коэффициент нулю, можно говорить об отсутствии связи.
– Коэффициент Фихнера – используют при небольшом объеме исходной информации, его пределы [–1; +1]:
 ,
,
 – количество совпадений знаков отклонений индивидуальных величин факторного и результативного признаков от их средней арифметической величины.
– количество совпадений знаков отклонений индивидуальных величин факторного и результативного признаков от их средней арифметической величины.
– Коэффициент ассоциации Д. Юла – для альтернативных признаков:
Таблица 25
Таблица «четырех полей»
| Признаки | А (да) |  (нет) (нет)
| Итого |
| В (да) | a | b | a+b |
 (нет) (нет)
| c | d | c+d |
| Итого | a+c | b+d | n |
 .
.
– Коэффициент контингенции К. Пирсона – для качественных (альтернативных) признаков ([–1; +1]):
 .
.
– Коэффициент взаимной сопряженности К. Пирсона – для альтернативных признаков, принимающих любое число вариантов значений, лежит в пределах [0; +1].
Для коэффициентов взаимной сопряженности составляется таблица 26
Таблица 26
Таблица первичной информации
| Признаки | А | B | C | Итого |
| D | f11 | f12 | f13 | A1i |
| E | f21 | f22 | f23 | A2i |
| F | f31 | f32 | f33 | A3i |
| Итого | A1j | A2j | A3j | n |
Затем вычисляется показатель средней квадратической сопряженности.
 ,
,
где  – частоты каждой клетки;
– частоты каждой клетки;  – номер строки;
– номер строки;  – итоговые частоты по строкам;
– итоговые частоты по строкам;  – итоговые частоты по графам.
– итоговые частоты по графам.
После чего вычисляются сами коэффициенты:
 .
.
– Коэффициент взаимной сопряженности А.А. Чупрова – при небольшом объеме исходной информации ([0; +1]).
 ,
,
где  – число групп по столбцам таблицы;
– число групп по столбцам таблицы;  – число групп по строкам таблицы.
– число групп по строкам таблицы.
– Эмпирическое корреляционное отношение – при любой форме зависимости ([0; +1]).
– Коэффициент корреляции рангов Спирмена – когда значения количественных признаков могут быть проранжированны ([–1; +1]);
 ,
,
где  – разность между величинами рангов признака-фактора и результативного признака;
– разность между величинами рангов признака-фактора и результативного признака;  – число показателей (рангов) изучаемого рода.
– число показателей (рангов) изучаемого рода.
Оценка существенности проводится по методам:
– t-критерий Стьюдента – при большом объеме выборки.
Находится расчетное значение

где  – линейный коэффициент корреляции.
– линейный коэффициент корреляции.
Полученное значение сравнивается с табличным и если  , то можно говорить о существенной зависимости между рассматриваемыми признаками;
, то можно говорить о существенной зависимости между рассматриваемыми признаками;
– метод преобразованной корреляции Фишера – по данным малой выборки (данный метод был рассмотрен в теме «Выборочное наблюдение»).
6. Построение модели связи (уравнения регрессии, параметры которого вычисляются по методу наименьших квадратов).
Уравнение регрессии достаточно хорошо отображает изучаемую взаимосвязь, если отношение средней квадратической ошибки уравнения к среднему уравнению результативного признака не превышает 10-15%.
7. Определение коэффициента эластичности
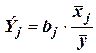 ,
,
где  –коэффициент регрессии при
–коэффициент регрессии при  -м факторе. Коэффициент эластичности показывает на сколько процентов в среднем изменяется результативный признак с изменением признака-фактора на 1 %.
-м факторе. Коэффициент эластичности показывает на сколько процентов в среднем изменяется результативный признак с изменением признака-фактора на 1 %.
Так же для сравнения роли различных факторов можно применить β – коэффициента (показывает на какую часть среднего квадратическо отклонения изменится результативный показатель при изменении соответствующего фактора на величину его среднего квадратического отклонения)
 .
.
Корреляционно-регрессионный анализ измеряет тесноту, направление связи и устанавливает форму связи. Он применим если: все признаки и их совместные распределения подчиняются нормальному закону распределения; дисперсия моделируемого признака в течении всего изучаемого периода оставаться постоянной при изменении величины и значений факторных признаков; отдельные наблюдения являются независимыми. Этапы составления корреляционно-регрессионной модели: логический анализ сущности изучаемого явления и его причинно-следственных связей; установление результативного показателя и факторов, влияющие на его изменение; сбор первичной информации и проверка ее на однородность и нормальность распределения; исключение из массива первичной информации всех аномальных единиц; установление факта наличия корреляционной зависимости между результативным и факторным признаками и определение ее характера и направления; измерение степени тесноты связи и оценка ее существенности; построение модели связи (уравнения регрессии, на основе метода наименьших квадратов); определение того, действительно ли уравнение регрессии достаточно хорошо отображает изучаемую взаимосвязь; определение коэффициента эластичности.
Список литературы
Основная:
1. Статистика : учеб. пособие / Н. М. Гореева и др. ; под ред. С. А. Орехова .– М. : Эксмо, 2010 .– 208с. – (Учебный курс: кратко и доступно) .– Библиогр.: с.204-205.
2. Статистика : учебник / И.И. Елисеева [и др.] ; Санкт-Петербурский государственный университет экономики и финансов; под ред. И.И. Елисеевой .– М. : Изд-во Юрайт : ИД Юрайт, 2011 .– 565 с. : ил. – (Основы наук) .– Библиогр.: с.564-565.
3. Социально-экономическая статистика: Учебное пособие / Я.С. Мелкумов. – 2-e изд. – М.: НИЦ Инфра-М, 2013. – 186 с.
4. Экономическая статистика: Учебник / Под ред. проф. Ю.Н. Иванова. – 4-e изд., перераб. и доп. – М.: НИЦ Инфра-М, 2013. – 668 с.
5. Статистика промышленности: Учебное пособие / А.А. Тумасян, Л.И. Василевская. – М.: НИЦ Инфра-М; Мн.: Нов. знание, 2012. – 430 с.
Дополнительная:
1. Статистика: Учебник / А.М. Годин. – 10-e изд., перераб. и испр. – М.: Дашков и К, 2012. – 452 с.
2. Бородкин, Ф. М. Социальные индикаторы [Электронный ресурс] : учебник для студентов вузов, обучающихся по специальности «Статистика» и другим экономическим специальностям / Ф. М. Бородкин, С. А. Айвазян. – М.: ЮНИТИ-ДАНА, 2012. – 607 с.
3. Гусаров, В. М. Статистика [Электронный ресурс] : учеб. пособие для студентов вузов, обучающихся по экономическим специальностям / В. М. Гусаров, Е. И. Кузнецова. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2012. – 479 с.
4. Экономическая статистика: Учебник / Московский Государственный Университет им. М.В.Ломоносова (МГУ); Под ред. Ю.Н.Иванова – 4 изд., перераб. и доп. – М.: ИНФРА-М, 2011. – 668 с.
5. Социально-экономическая статистика: Учебное пособие / Я.С. Мелкумов. – М.: ИНФРА-М, 2008. – 236 с.
6. Статистика : учеб. пособие / А.В. Багат [и др.] ; под ред. В.М. Симчеры .– М. : Финансы и статистика, 2005 .– 368 с.
Подписано в печать 26.08.08. Формат 60х90 1/16
Гарнитура Times ET, 10. Усл. печ. л. – 2.
Тираж 200 экз.
Типография «Познание» ИЭУиП,
лицензия № 172 от 12.09.96 г.
420108, г. Казань, ул. Зайцева, д. 17.
Дата добавления: 2015-02-09; просмотров: 267; Мы поможем в написании вашей работы!; Нарушение авторских прав |