
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Идеальный газ. Параметры состояния идеального газа.
Примером простейшей системы, изучаемой в молекулярной физике, является газ. Согласно статистическому подходу газы рассматриваются как системы, состоящие из очень большого числа частиц (до 1026 м–3), находящихся в постоянном беспорядочном движении. В молекулярно-кинетической теории пользуются моделью идеального газа, согласно которой считают, что:
1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;
2) между молекулами газа отсутствуют силы взаимодействия;
3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Оценим расстояния между молекулами в газе. При нормальных условиях (н.у.: р=1,03·105 Па; t=0ºС) число молекул в единице объема: 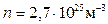 . Тогда средний объем, приходящийся на одну молекулу:
. Тогда средний объем, приходящийся на одну молекулу:
 (м3).
(м3).
Среднее расстояние между молекулами: 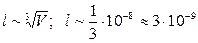 м. Средний диаметр молекулы: d»3·10-10 м. Собственные размеры молекулы малы по сравнению с расстоянием между ними (в 10 раз). Следовательно, частицы (молекулы) настолько малы, что их можно уподобить материальным точкам.
м. Средний диаметр молекулы: d»3·10-10 м. Собственные размеры молекулы малы по сравнению с расстоянием между ними (в 10 раз). Следовательно, частицы (молекулы) настолько малы, что их можно уподобить материальным точкам.
В газе молекулы большую часть времени находятся так далеко друг от друга, что силы взаимодействия между ними практически равны нулю. Можно считать, что кинетическая энергия молекул газа много больше потенциальной, поэтому последней можно пренебречь.
Однако в моменты кратковременного взаимодействия (столкновения) силы взаимодействия могут быть значительными, что приводит к обмену энергией и импульсом между молекулами. Столкновения служат тем механизмом, с помощью которого макросистема может переходить из одного доступного ей при данных условиях энергетического состояния в другое.
Модель идеального газа можно использовать при изучении реальных газов, так как они в условиях, близких к нормальным (например, кислород водород, азот, углекислый газ, пары воды, гелий), а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу.
Состояние тела может измениться при нагреве, сжатии, изменении формы, то есть при изменении каких - либо параметров. Различают равновесные и неравновесные состояния системы. Равновесное состояние – это состояние, при котором все параметры системы не меняются со временем (в противном случае - это неравновесное состояние), и нет сил, способных изменить параметры.
Важнейшими параметрами состояния системы являются плотность тела (или величина обратная плотности – удельный объем), давление и температура. Плотность (r) – масса вещества в единице объема. Давление (р – сила, действующая на единицу площади поверхности тела, направленная по нормали к этой поверхности. Разность температур (DТ) – мера отклонения тел от состояния теплового равновесия. Существует температура эмпирическая и абсолютная. Эмпирическая температура (t) – мера отклонения тел от состояния теплового равновесия с тающим льдом, находящимся под давлением в одну физическую атмосферу. В качестве единицы измерения принят 1 градус Цельсия (1 оС), который определен тем условием, что тающему под атмосферным давлением льду приписывают 0 оС, а кипению воды при том же давлении – 100 оС, соответственно. Различие между абсолютной и эмпирической температурой заключается, прежде всего, в том, что абсолютная температура отсчитывается от предельно низкой температуры – абсолютного нуля, который лежит ниже температуры таяния льда на 273,16о, то есть
| T = t + 273,16. | (6.2.1) |
В термодинамике часто количество вещества определяют в грамм-молекулах (количество вещества, выраженное в граммах, численно равное его молекулярному весу). Грамм-молекулу называют молем. Объем одного моля – молярный объем. 1000 молей соответствует киломолю.
Три основных параметра: r, Р и Т или V, Р и Т - не являются независимыми. Они связаны уравнением, которое называют уравнением состояния:
| f (р,V,T) = 0, | (6.2.2,а) |
или
| р = f (V,T). | (6.2.2,б) |
Отметим, что любая функциональная зависимость, связывающая между собой термодинамические параметры подобно (6.2.2,а), называется также уравнением состояния. Вид функции зависимости между параметрами ((6.2.2,а), (6.2.2,б)) определяется для каждого вещества экспериментально. Однако до сих пор удалось определить уравнение состояния только для газов, находящихся в разряженных состояниях, и, в приближенной форме, для некоторых сжатых газов.
Дата добавления: 2015-02-09; просмотров: 358; Мы поможем в написании вашей работы!; Нарушение авторских прав |