Реальные газы. Уравнение Ван-дер-Ваальса

Поведение реальных газов довольно хорошо описывается уравнением Менделеева-Клайперона, т.е. уравнением состояния идеального газа

, (9.1.1)

только при не слишком высоких давлениях и достаточно высоких температурах.

С повышением давления и уменьшением температуры наблюдается значительное отступление от этого уравнения, т.е. с повышением давления поведение реальных газов отклоняется от поведения газов идеальных. Например, рассмотрим произведение pV для массы азота, занимающей при нормальных условиях объем, равный одному литру. В соответствии с уравнением (9.1.1) pV при неизменной температуре должно оставаться постоянным.

Рассматривая график, мы видим, что реальный газ при увеличении давления первоначально сжимается больше, чем это следует из уравнения идеальных газов, так что произведение pV уменьшается с возрастанием давления. При дальнейшем увеличении давления начинают сказываться какие-то иные свойства молекул реальных газов, в силу которых произведение pV возрастает. Причины подобных отклонений заключаются в следующем:

1) большую сжимаемость реального газа по сравнению с идеальным газом обуславливают силы межмолекулярного взаимодействия; молекулярное сцепление приводит к возникновению как бы добавочного давления, возрастающего при увеличении плотности газа;

2) наблюдаемое при высоких давлениях уменьшение сжимаемости и соответствующее возрастание произведения pV объясняется тем, что реальные молекулы не являются материальными точками, а обладают некоторым конечным объемом.

По мере увеличения давления возрастает плотность газа, а вместе с ней возрастает влияние собственного объема молекул – газ оказывает большее сопротивление сжатию, чем это следует из уравнения Клайперона.

Уравнение состояния реального газа было предложено впервые голландским физиком Ван-дер-Ваальсом (1837-1929) и носит его имя. Уравнение Ван-дер-Ваальса отличается от уравнения Клайперона наличием двух поправочных членов, один из которых учитывает влияние собственного объема молекул, а другой – влияние сил молекулярного притяжения.

Рассмотрим подробнее каждый из этих поправочных членов.

Рассчитаем поправку на недоступный объем. Молекула идеального газа, заключенная в некотором сосуде, может находиться в любой его точке и для нее доступен весь объем сосуда V.

Молекула реального газа не может находиться в тех местах сосуда, где расположены остальные (N-1)-молекул и ей доступна лишь часть всего объема, равная (V-b), где b - объем, недоступный для молекул. Для подсчета этого недоступного объема будем считать, что в газе происходят только двойные соударения молекул. Для каждой пары взаимодействующих молекул недоступной является та часть объема, в которой расстояние между их центрами равно d, где d - диаметр молекулы, т.е. сфера с объемом 4/3pd³. Из N-молекул может быть образовано 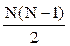пар. Следовательно, полный недоступный объем для всех молекул равен

.

На каждую из N -молекул приходится

, т.е. .

С учетом введенной поправки уравнение состояния реального газа примет вид

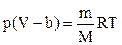
при T=const p(V-b)=const.

График этой зависимости изображен на рис. 9.2

Рассчитаем поправку на «внутреннее давление» (точнее на влияние сил межмолекулярного притяжения). Сила давления газа на стенку сосуда – есть результат многочисленных столкновений молекул с твердой поверхностью. Поэтому давление идеального газа прямо пропорционально концентрации молекул n в слое, прилежащем непосредственно к стенке:

n = N/V.

Так как между молекулами газа действуют силы притяжения, то давление уменьшается на величину p¢. Поскольку силы взаимодействия очень быстро убывают с расстоянием, то практически следует учитывать притяжение первого слоя лишь одним соседним слоем. Сила этого притяжения, рассчитанная на единицу площади, пропорциональна концентрации молекул в обоих слоях:

.

Обозначим коэффициент пропорциональности a, тогда

.

Обозначим aN²=a, тогда p¢=a/V². Вид коэффициента a зависит от конкретного строения взаимодействующих молекул, т.е. от природы газа. Объединяя вторую поправку с первой, мы можем записать

или

- уравнение Ван-дер-Ваальса.

В этом уравнении V - объем, занимаемый m -граммами газа. Поскольку при выводе уравнения был сделан целый ряд упрощений, на него следует смотреть как на приближенное уравнение состояния реального газа.

Вычисленные с помощью уравнения Ван-дер-Ваальса значения давления газа, достаточно точно совпадает с опытом лишь при относительно высоких температурах и только в некотором интервале давлений.