
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Электрический диполь. Расчет напряженности электростатического поля диполя с помощью принципа наложения полей.
 |
Рассмотрим два точечных заряда +q и –q, жестко связанных между собой и смещенных на расстояние l друг от друга. Смещение обоих зарядов будем характеризовать вектором l, направленным от отрицательного заряда к положительному. Такую пару зарядов называют электрическим диполем (рис.10.6).
Небольшое проводящее тело в электрическом поле можно приближенно рассматривать как диполь, так как на его концах возникают индукционные заряды, равные по модулю и противоположные по знаку. Многие молекулы построены из положительных и отрицательных ионов, центры которых смещены друг относительно друга, поэтому молекулы также можно считать во многих случаях электрическими диполями. Принцип наложения полей был использован для расчета электростатического поля диполя.
Введем некоторые определения.
Плечом диполя называется вектор l направленный по оси диполя от отрицательного заряда к положительному и численно равный расстоянию между ними (рис. 10.6). Произведение положительного заряда диполя q на плечо l называется электрическим моментом диполя ре:
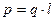 . .
|
Вектор pе совпадает по направлению с плечом диполя l.
В соответствии с принципом суперпозиции полей напряженность в произвольной точке поля диполя
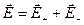 , (10.3.1)
, (10.3.1)
где 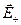 и
и  — напряженности полей, создаваемых положительным (+q)и отрицательным ( – q) зарядами.
— напряженности полей, создаваемых положительным (+q)и отрицательным ( – q) зарядами.
 |
Если точка А расположена на оси диполя (рис. 10.7), то векторы
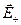 и
и  направлены также вдоль этой оси, но в противоположные стороны.
направлены также вдоль этой оси, но в противоположные стороны.
По формуле напряженности точечного заряда
 ,
,  (10.3.2)
(10.3.2)
где r1 и r2 — радиусы-векторы, проведенные в точку А из концов диполя +q и —q, причем они совпадают по направлению с вектором l, поэтому
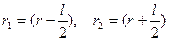
Следовательно,
 ,
, 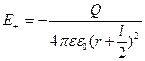 (10.3.3)
(10.3.3)
Тогда результирующая напряженность
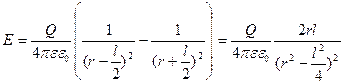 .
.
учитывая формулу определения диполя, получим

Если r>>l, то членом  по сравнению с r2 можно пренебречь.
по сравнению с r2 можно пренебречь.
Тогда
 . (10.3.4)
. (10.3.4)
Данная формула определяет напряженность диполя в точке, расположенной на его оси.
Дата добавления: 2015-02-09; просмотров: 571; Мы поможем в написании вашей работы!; Нарушение авторских прав |