
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифракционная решетка. Дифракция на одно-, двух-, трехмерных структурах. Уравнение Вульфа - Брэггов. Понятие о голографии.
Дифракционная решетка представляет собой совокупность одинаковых щелей, расположенных на одном расстоянии друг от друга.
Виды дифракционной решетки:
1) одномерная – совокупность щелей расположенных вдоль одной прямой;
2) двумерная – совокупность щелей, расположенных вдоль двух взаимно перпендикулярных направлениях, т.е. на плоскости щелей;
3) трехмерная – совокупность щелей, которые расположены вдоль трех взаимно перпендикулярных направлениях, т.е. в объеме.
Дифракция света на одномерной дифракционной решетке. Одномерная дифракционная решетка представляет собой систему из большого числа N одинаковых по ширине и параллельных друг другу щелей в экране, разделенных также одинаковыми по ширине непрозрачными промежутками.
Величина d = а + b называется постоянной, или периодом, дифракционной решетки, где а - ширина непрозрачного промежутка, b - ширина щели.
При расчете дифракционной картины на экране, установленном в фокальной плоскости собирающей линзы, необходимо учитывать интерференцию вторичных волн как от разных участков одной щели, так и от разных щелей решетки. Если плоская монохроматическая волна падает нормально на решетку, то колебания во всех точках щелей происходят в одинаковой фазе.
Колебания, возбуждаемые в произвольной точке, фокальной плоскости линзы каждой из щелей, совпадают по амплитуде и отличаются по фазе. Для каждой пары соседних щелей сдвиг фаз Δφ0 между этими колебаниями одинаков. Он зависит от длины волны λ и разности хода лучей от сходственных точек щелей:
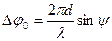
Главные, минимумы при дифракции света на дифракционной решетке наблюдаются под углами дифракции, соответствующими интерференционным минимумам при дифракции на одной щели:
 .
.
В этих точках интенсивность, создаваемая каждой из этих щелей в отдельности, равна нулю.
Главным максимумам соответствуют углы дифракции, удовлетворяющие условию:
d sin φ = ± nλ,
где n = 0, 1, 2, ... — порядок главного максимума.
При освещении решетки белым светом на экране наблюдается неокрашенный центральный максимум нулевого порядка, а по обе стороны от него — дифракционные спектры 1-го, 2-го и т. д. порядков. Спектры имеют вид радужных полосок, в которых наблюдается непрерывный переход от окраски сине-фиолетового цвета у внутреннего края спектра к красной у внешнего края.
Поставим две дифракционные решетки одну за другой так, чтобы их штрихи были взаимно перпендикулярными. Первая решетка (штрихи которой, скажем, вертикальны) даст в горизонтальном направлении ряд максимумов, положения которых определяются условием

Вторая решетка (с горизонтальными штрихами) разобьет каждый из образовавшихся таким образом пучков на расположенные по вертикали максимумы, положения которых определяются условием

В итоге дифракционная картина будет иметь вид правильно расположенных пятен, каждому из которых соответствуют два целочисленных индекса m1 и m2.
Рассмотрим кристалл как совокупность параллельных кристаллографических плоскостей (плоскостей, в которых лежат узлы кристаллической решетки), отстоящих друг от друга на расстояние d.
Полагаем, что при падении рентгеновского излучения на кристалл происходит частичное отражение излучения от этих плоскостей. Вторичные волны, отразившиеся от разных плоскостей, когерентны и будут интерферировать между собой. Разность хода двух волн, отразившихся от соседних плоскостей, равна 2dsinθ, где q – угол, называемый углом скольжения падающих лучей. Максимумы интенсивности (дифракционные максимумы) наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе. Эти направления определяются условием
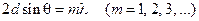 .
.
Это соотношение называется уравнением Вульфа-Брэгга.
Кристаллографические плоскости можно провести в кристалле множеством способов. Каждая система плоскостей может дать дифракционный максимум, если для нее окажется выполненным условие Вульфа-Брегга. Однако заметную интенсивность имеет лишь те максимумы, которые дают плоскости с густо расположенными узлами.
Дифракция рентгеновских лучей от кристаллов находит два основных применения. Она используется для исследования спектрального состава рентгеновского излучения (рентгеновская спектроскопия) и для изучения структуры кристаллов (рентгеноструктурный анализ). Определяя направления максимумов, получающихся при дифракции исследуемого рентгеновского излучения от кристаллов с известной структурой, можно вычислить длины волн. Наблюдая дифракцию рентгеновских лучей известной длины волны на кристалле неизвестного строения можно найти межплоскостные расстояния и расшифровать структуру кристалла.
Пространственной, или трехмерной, дифракционной решеткой называется такая оптически неоднородная среда, неоднородности которой периодически повторяются при изменении всех трех пространственных координат. Примером пространственной дифракционной решетки может служить кристаллическая решетка твердого тела. Частицы, находящиеся в узлах этой решетки (атомы, молекулы или ионы), играют роль упорядоченно расположенных центров, когерентно рассеивающих падающий на них свет. Пусть d1, d2 d3 - периоды решетки по трем осям координат x, y, z, которые проведены вдоль трех ребер решетки, пересекающихся в каком-либо из ее узлов. Тогда при дифракции Фраунгофера главные максимумы удовлетворяют условиям Лауэ
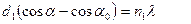
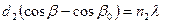
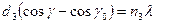 ,
,
где α0, β0, γ0 и α, β, γ - углы между осями координат x, y, z, и направлениями распространения соответственно падающего и дифрагировавшего света; n1, n2 и n3 - целые числа, определяющие порядок максимума, λ - длина волны света. Условия Лауэ вытекают из соотношения для дифракционных максимумов при наклонном падении света на одномерную дифракционную решетку.
Голография есть особый способ записи и последующего восстановления изображения предмета, основанный на регистрации интерференционной картины. При освещении фотопластинки (голограммы) пучком света изображение предмета восстанавливается в почти первоначальном виде, так что создается ощущение его реальности.
Для записи предмета на светочувствительной пластинке кроме волны, отраженной от предмета (так называемой предметной волны), используется когерентная с ней волна от источника света (так называемая опорная волна). На фотопластинке фиксируется распределение интенсивности в интерференционной картине, возникающей при наложении предметной и опорной волн. При освещении проявленной фотопластинки происходит дифракция света в фотослое. В результате дифракции восстанавливается изображения предмета.
Цветная голография основана на записи объемной интерференционной картины. Восстановление изображения происходит при отражении света от голограммы. При записи предмет (последовательно или одновременно) освещается излучением трех цветов: красным, зеленым и синим. В толще фотоэмульсии образуется (и фиксируются) три пространственные интерференционные картины. При освещении белым цветом каждая из систем формирует свое одноцветное изображение предмета. В результате, при наложении трех одноцветных, получаются цветное изображение предмета.
Дата добавления: 2015-02-09; просмотров: 379; Мы поможем в написании вашей работы!; Нарушение авторских прав |