
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание состояния квантовой частицы. Волновая функция, ее статистический смысл. Условие нормировки. Уравнение Шредингера.
Положение частицы в пространстве в данный момент времени определяется в квантовой механике заданием волновой функции (пси-функции) Ψ (х, у, z, t). Вероятность dw того, что частица находится в момент времени t в малом объеме dV вблизи точки М (х, у, z), равна:

где  — квадрат модуля Ψ-функции:
— квадрат модуля Ψ-функции:  . Здесь
. Здесь  —функция, комплексно сопряженная с Ψ. Величина
—функция, комплексно сопряженная с Ψ. Величина  есть плотность вероятности пребывания частицы в данной точке пространства:
есть плотность вероятности пребывания частицы в данной точке пространства:
 (22.4.1)
(22.4.1)
Интенсивность волны де Бройля определяется величиной  .
.
Из определения Ψ-функции следует условие нормировки вероятностей:
 (22.4.2)
(22.4.2)
где тройной интеграл по объему вычисляется по координатам х, у и z от -  до +
до +  , т. е, по всему бесконечному пространству. Условие нормировки указывает на то, что пребывание частицы где-либо в пространстве есть достоверное событие и его вероятность должна быть равна единице.
, т. е, по всему бесконечному пространству. Условие нормировки указывает на то, что пребывание частицы где-либо в пространстве есть достоверное событие и его вероятность должна быть равна единице.
Волновая функция Ψ(х,у,z,t) является основной характеристикой состояния микрообъектов (атомов, молекул, элементарных частиц). С ее помощью вычисляется среднее значение физической величины L, характеризующей объект, находящийся в состоянии, описываемом волновой функцией Ψ
 (22.4.3)
(22.4.3)
где <L> — среднее значение величины L.
Временным уравнением Шредингера называется основное дифференциальное уравнение квантовой механики относительно волновой функции Ψ(х, у, z, t) (оно не выводится, а является фундаментальным и основано на тех экспериментальных результатах, которые были накоплены при изучении микрообъектов). Временное уравнение определяет Ψ-функцию для микрочастиц, движущихся в силовом поле с потенциальной энергией U(x, у, z, t) со скоростью υ<<с, где с — скорость света в вакууме.
Уравнение Шредингера имеет вид
 , (22.4.4)
, (22.4.4)
где Δ — оператор Лапласа 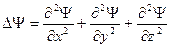 , т — масса частицы,
, т — масса частицы, 
h —постоянная Планка,  - мнимая единица.
- мнимая единица.
Уравнение Шредингера дополняется условиями, которые накладываются на Ψ-функцию:
а) функция Ψ должна быть конечной, однозначной и непрерывной;
б) производные 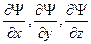 должны быть непрерывны;
должны быть непрерывны;
в) функция  должна быть интегрируема, т. е. интеграл
должна быть интегрируема, т. е. интеграл 
 должен быть конечным.
должен быть конечным.
В случае, когда функция потенциальной энергии U не зависит от времени ( 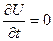 ) решение временного уравнения Шредингера имеет вид:
) решение временного уравнения Шредингера имеет вид:

причем координатная часть волновой функции Ψ(х, у, z) удовлетворяет стационарному уравнению Шредингера:
 (22.4.5)
(22.4.5)
где W — энергия частицы.. Функции Ψ, удовлетворяющие уравнению Шредингера при заданном виде U =U{x, у, z), называются собственными функциями. Они существуют лишь при определенных значениях энергии W, называемых собственными значениями энергии. Совокупность собственных значений W образует энергетический спектр частицы. В зависимости от вида функции U {х, у, z) энергетический спектр частицы может быть дискретным или непрерывным. Отыскание собственных значений и собственных функций составляет важнейшую задачу квантовой механики.
Если частица находится в определенном энергетическом состоянии с энергией W = const, то вероятность dw обнаружить ее в элементе объема dV не зависит от времени:

Такое состояние частицы называется стационарным состоянием. Атом, находящийся в стационарном состоянии, имеет постоянную энергию и не излучает электромагнитные волны.
Дата добавления: 2015-02-09; просмотров: 324; Мы поможем в написании вашей работы!; Нарушение авторских прав |