Определение: Вхождение домена в отношение принято называть атрибутом. Строки отношения называют картежами.

Количество атрибутов в отношении называется степенью, или рангом отношения. В отношении не может быть одинаковых кортежей.

Два отношения будут одинаковые, если отличаются порядком строк или столбцов.

Определение: Схемойотношения R называется перечень имён атрибутов данного отношения с указанием домена к которому они относятся: S_R= (A1, A2,…, An) A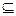i Di

Определение:Если атрибуты принимают значения из одного и того же домена, то они называются - сравнимыми(тета), где - множество допустимых операций сравнения, заданных для данного домена.

Пример: Если домен содержит числовые данные, то для него допустимы все операции сравнения, тогда ={=,<>,>=, <=}.

Определение:Схемы двух отношений называются эквивалентными, если они имеют одинаковую степень и возможно такое упорядочение имён атрибутов в схемах отношений, что на одинаковых местах будут находиться сравнимые атрибуты, т.е. атрибуты, принимающие значения из одного домена.

S_R1= (A1, A2,…, An) – схема отношения R1, S_R2= (Bi1, Bi2,…, Bin) – схема отношения R2,

после упорядочения атрибутов. Тогда

S_{R1 ~} S_R2 <=>

В реляционной модели поддерживаются иерархические связи между отношениями. В каждой связи одно отношение может выступать как основное, а другое в роли подчиненного. Один кортеж основного отношения может быть связан с несколькими кортежами подчиненного отношения. Для поддержки этих связей оба отношения должны содержать наборы атрибутов, по которым они будут связаны.

Первичный ключ –PRIMARY KEY, внешний ключ- FOREIGN KEY.

Определение:Объединением двух отношений называется отношение, содержащее множество кортежей, принадлежащих либо первому, либо второму исходным отношениям, либо обоим отношениям одновременно.

Пусть заданы два отношения R₁={r₁}, R₂={r₂}, где r₁ и r₂ –соответственно кортежи отношений R₁ и R₂ , то объединение

R₃=R₁ È R₂ = {г/ rÎ R₁ Ú rÎ R₂},

здесь r –кортеж нового отношения, Ú- операция логического сложения «Или».

Определение:Пересечением отношений называется отношение, которое содержит множество кортежей, принадлежащих одновременно первому и второму отношениям (R₁ и R₂):

R₄=R₁ Ç R₂ = {г/ rÎ R₁ Ù rÎ R₂}, здесь Ù -логическое умножение «И».

Определение:Разностью отношений R₁ и R₂ называется отношение, содержащее множество кортежей, принадлежащих R₁ и не принадлежащих R₂ :

R₅=R₁ \R₂ = {г/ rÎ R₁ Ù rÏ R₂}.

Операции объединения и пересечения являются коммутативными операциями, т.е. результат операции не зависит от порядка аргументов в операции. Операция разность является принципиально не симметричной, т.е. результат операции будет различным для разного порядка аргументов.

Пример: Рассмотрим примеры с использованием операций. Даны отношения R_1,R₂ и R_3, имеют эквивалентные схемы.

R₁ = (ФИО, Паспорт, Школа), R₂ = (ФИО, Паспорт, Школа), R₃ = (ФИО, Паспорт, Школа),

R₁- содержит список абитуриентов, сдавших репетиционные экзамены,

R₂- содержит список абитуриентов, сдавших экзамены на общих условиях,

R₃- содержит список абитуриентов, принятых в институт.

При неудачной сдаче репетиционных экзаменов абитуриент мог делать вторую попытку и сдавать экзамены в общем потоке, поэтому абитуриенты могут присутствовать как в первом, так во втором потоке.

Получить списки абитуриентов, отвечающие следующим условиям:

1. Список абитуриентов, которые поступали два раза:

R = R₁ Ç R₂,

2. Список абитуриентов первого и второго потока:

R = R₁ È R₂,

3. Список абитуриентов, которые поступали два раза и не поступили в Вуз:

R = R₁ È R₂\ R₃,

4. Список абитуриентов, которые поступили в Вуз с первого раза:

R = (R₁ \ R₂Ç R₃) È (R₂ \ R₁Ç R₃),

5. Список абитуриентов, которые поступили в Вуз только со второго раза:

R = R₁ Ç R₂Ç R₃,

6. Список абитуриентов, которые не поступили из первого потока:

R = R₁ \R₃,

7. Список абитуриентов, которые не поступили из второго потока:

R = R₂ \R₃,

8. Список абитуриентов, которые поступали только один раз и не поступили:

R = (R₁ \ R₂) È (R₂ \ R₁)\ R₃.

Определение: Операции объединения, пересечения и разности применимы только к отношениям с эквивалентными схемами.

Определение: сцеплением или конкатенацией, с =< c _1, c _{2, …,}c _n > и q =< q _1,q _{2, …,}q _m >называется кортеж, полученный добавлением значений второго в конец первого (обозначение сцепления (с,q)):

(с,q) = < c _1, c _{2, …,}c _n, q _1,q _{2, …,}q _m,> , где n и m- число элементов в первом и втором кортеже.

Операция декартова произведения, меняет степень результирующего отношения.