
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Диаграммы SFC
В семействе МЭК-языков SFC (Sequential Function Chart –последовательная функциональная схемаt) диаграммы стоят особняком, а точнее, выше по отношению к остальным четырем языкам. Диаграммы SFC являются высокоуровневым графическим инструментом. Благодаря SFC идея превращения модели системы в законченную программу стала реальностью. В отличие от применения вспомогательных средств моделирования SFC дает действующий непосредственно в ПЛК прототип.
Заслуга первой практической реализации языка этапов и переходов для ПЛК принадлежит французским фирмам. Совместная работа изготовителей ПЛК и объединения пользователей привела к появлению национального стандарта «Графсет» и международного стандарта МЭК 848 (1988 г.). МЭК 61131-3 заимствовал «Графсет» с некоторыми доработками.
Оригинальный метод формального описания дискретных систем был предложен Карлом Адамом Петри в 1962 году. Он опирается на разделение системы или отдельных ее частей на множество простых позиций. Позиция описывает состояние части системы. Причем состояние понимается здесь достаточно гибко, это может быть состояние оборудования, процесса или программы. Переходы между позициями происходят при выполнении определенных условий. Графически позиция отображается в виде окружности (см. рис. 7.2). Переходам соответствуют отрезки, соединенные с позициями направленными дугами. Каждая позиция способна обладать маркером и передавать его другим позициям по исходящим дугам. Маркеры отображается в виде жирной точки. Допускается одновременное присутствие нескольких маркеров. В настоящее время отождествлять SFC с сетями Петри уже нельзя.
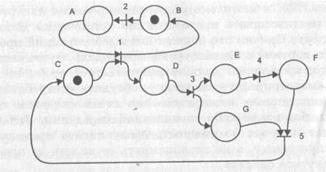 |
Рис. 7.2. Сеть Петри
SFC-диаграммы
В отличие от сетей Петри дуги в SFC имеют выраженную направленность сверху вниз и отражаются прямыми линиями. Позиции в SFC называют шагами или этапами. На диаграмме они отражаются в виде прямоугольников. Благодаря такому «кубизму» существует возможность реализации диаграмм в символах псевдографики (рис. 7.3). Задать несколько стартовых шагов в SFC нельзя, только один шаг диаграммы является начальным.

Рис. 7.3. SFC-диаграмма, выполненная символами псевдографики (условие перехода — язык IL)
Графическая диаграмма SFC состоит из шагов и переходов между ними. Разрешение перехода определяется условием. С шагом связаны определенные действия. Описания действий выполняются на любом языке МЭК. Сам SFC не содержит каких-либо управляющих команд ПЛК. Действия могут быть описаны и в виде вложенной SFC-схемы. Можно создать несколько уровней подобных вложений, но в конечном счете действия нижнего уровня все равно необходимо будет описать на IL, ST, LD или FBD.
Целью применения SFC является разделение задачи на простые этапы с формально определенной логикой работы системы. SFC дает возможность быстрого построения прототипа системы без программирования. Причем для отработки верхнего уровня не требуется детальное описание действий, так же как и привязка к конкретным аппаратным средствам.
Дата добавления: 2015-02-09; просмотров: 267; Мы поможем в написании вашей работы!; Нарушение авторских прав |