Уравнение Ходжкина -Хаксли.

Впервые материальная модель распределения нервного импульса в аксоне была предложена в 1961 г. Ходжкином и Хаксли. При построении математической модели распределения импульсов в активной среде необходимо учитывать изменение проводимости мембран для ионов калия, натрия и некоторых других видов ионов. Для этого в модели использовались проводимость мембран для различных ионов. Построение модели опиралось на два предложения:

1. Ионы калия проникают через мембрану при сдвиге потенциала до критического льшь тогда, когда вблизи калиевого канала присутствуют 4 активирующие этот процесс частицы.

максимальное удельная электропроводимость мембраны при всех открытых калиевых каналов.

h – вероятность подхода к каналу одной активной части.

2. Ионы натрия проникают через мембрану лишь в том случае, если в близи канала находится 3 активных частицы и одна блокирующая.

мах. удельная электропроводимость мембран при всех открытых натриевых каналов.

m – вероятность подхода к каналу одной активной частоты.

n – вероятность подхода к каналу одной блокирующей частицы.

На основании экспериментальных данных, а именно за счёт измерения токов через мембрану гигантского аксона при различных напряжениях, было установлено, что суммарный ток мембраны складывается из следующих токов:

- ток смещения

- ёмкость.

- ток ионов калия

- ток ионов натрия

Суммарный ток возникающий за счёт других ионов.

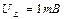
Т.о. полный ток

Т.о. ток через мембрану зависит от приложенного напряжения и от вероятности подхода активирующих и блокирующих частиц к ионным каналом. Для их определения была использована следующая система уравнений составленная из законов кинетики:

- константа которая зависит от потенциала на мембране и могут быть определены экспериментально. В зависимости от значений напряжений изменяются величины коэффициентов и соответственно изменяется вклад в общий ток тех или иных ионов, так при достижении потенциала 112мВ происходило открытие каналов Na, при других потенциалах больший вклад давали ионы К.

Нервное волокно можно представить в виде эквивалентной элементарной схемы с распределёнными параметрами в качестве активного сопротивления, увеличивающего амплитуду сигналов вводится генератором ионов K, Na и др. т.е. схема может быть представлена:

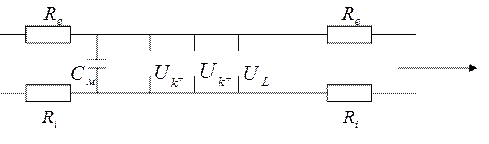
Уравнение распространения нервного импульса вдоль такой линии с некоторой константой скоростью описывается волновым уравнением:

Для распределения импульса, вдоль волокна который соответствует форме нервного волокна.

Сила тока в волноводе имеет вид:

х – координата, вдоль которой, распространяется волна.

- сопротивление цитоплазмы.

Объединяя полученное выражение, для силы тока Х и х получим уравнение для определения скорости:

В соответствии с уравнением теоретически получено значение скорости распространения, экспериментально получим значение