Основные законы цепей постоянного тока

Закон Ома. В 1826 году немецкий физик Г. Ом экспериментально установил, что величина (сила) тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника (рис. 2.16)

Рис.2.16. Элемент электрической цепи – резистор

I = (φ_a – φ_b)/R = U_ab/R,

где коэффициент пропорциональности R – const. Записанное выражение представляет собой математической записи закона Ома для участка цепи, не содержащего внутренних источников ЭДС (т.е. для пассивного участка цепи).

Оно читается так: сила тока на некотором участке электрической цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению этого участка.

Из записанного выражения следует, что

U_ab = IR,

т.е. напряжение на данном участке пропорционально протекающему по нему току.

Величина R называется электрическим сопротивлением, а участок цепи, обладающий сопротивлением – резистором. В системе СИ единицей электрического сопротивления проводников служит Ом. Сопротивлением в 1 Ом обладает участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.

Рассмотрим электрическую цепь, схема которой показана на рис. 2.17. Она состоит из двух участков: однородного (резистор R) и неоднородного (источник E и резистор r).

Рис. 2.17. Электрическая цепь постоянного тока

В соответствии с законом Ома для однородного (пассивного) участка

,

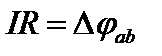а для неоднородного

.

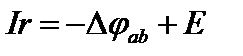Последнее выражение есть закон Ома для участка цепи, содержащего внутренние источники ЭДС (т.е. для активного участка цепи).

Просуммировав оба равенства, получим

,

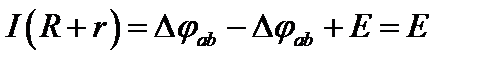откуда

.

Полученное выражение называют законом Ома для полной цепи.

Сопротивление r неоднородного участка на рис. 2.17 можно рассматривать как внутреннее сопротивление источника энергии.

Закон Ома можно сформулировать и относительно тока:

I = GU ,

где G – проводимость – величина, обратная сопротивлению

.

Проводимость измеряют в сименсах (См).

Обобщенный закон Ома для ветви, содержащей ЭДС (т.е. для активной ветви) определяется следующим образом. Определим потенциал точки a, исходя из потенциала φ_b. Рассчитаем изменение потенциала промежуточной точки с (рис. 2.18) по сравнению с φ_b .

Между точками b и c расположен источник ЭДС, поэтому потенциал точки с отличается от потенциала точки b на величину Е. Стрелка источника показывает направление увеличения потенциала. Следовательно, потенциал точки с

Рис. 2.18. Схема активной ветви

ниже потенциала точки b. Между точками с и а находится резистор сопротивлением R. Потенциал φ_a отличается от потенциала φ_c величиной напряжения на резисторе R∙I . Ток направлен от большего потенциала к меньшему, поэтому потенциал φ_a выше потенциала φ_c .

Таким образом

φ_a = φ_b − E + RI,

φ_a − φ_b = −E + RI,

но

φ_a − φ_b = U_ab ,

т. е.

U_ab = −E + R I.

Аналогичным образом можно определить напряжение между двумя любыми точками, рассчитав изменение потенциалов между ними. При этом нужно вести расчет в сторону увеличения потенциала, т. е. от второго индекса напряжения к первому.

Решим последнее уравнение относительно тока:

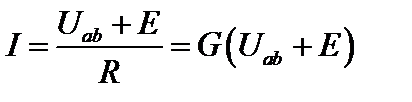
где - проводимость ветви.

Это выражение называют еще законом Ома для активной ветви.

Последнее выражение можно составить также исходя из следующих рассуждений. Для появления тока в ветви (рис. 2.18) есть два условия: наличие разности потенциалов между концами ветви и действие источника ЭДС. Если направления ЭДС и напряжения U_аb совпадают с направлением тока, они способствуют его появлению и должны быть записаны в уравнение со знаком плюс (рис. 2.19). В противном случае – со знаком минус.

Рис. 2.19. Правило расстановки знаков для ЭДС

Рассуждая таким образом, получим для тока ветви приведенное выше выражение.

Таким образом, в общем случае для активной цепи получаем

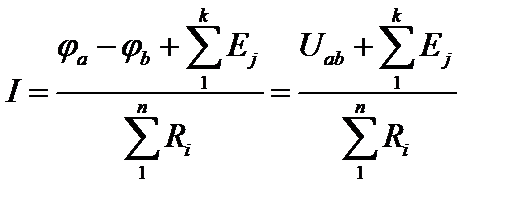
Пример 2.1. Записать закон Ома для активной цепи представленное на рисунке.

Решение.

.

■

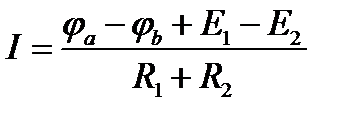Геометрической интерпретацией закона Ома является вольтамперная характеристика (ВАХ).

Законы Кирхгофа описывают соотношения между параметрами участков электрической цепи.

Первый закон Кирхгофасформулирован для узла электрической цепи. Напомним, что узел – это точка в схеме, где сходятся не менее трех ветвей (рис. 2.19).

Рис. 2.20. Схема узла электрической цепи

Общее описание первого закона Кирхгофа:

.

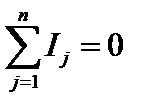Приведенное выражение читается так: алгебраическая сумма токов в узле равна нулю (принцип непрерывности тока).

Правило знаков: токи, одинаково направленные относительно узла, записывают с одинаковыми знаками (обычно токи, текущие к узлу считаются положительными, а от узла - отрицательными).

Иногда первый закон Кирхгофа формулируют по-другому: сумма токов, подходящих к узлу, равна сумме токов, отходящих от узла:

или

.

Первый закон Кирхгофа по сути является законом баланса токов в узлах цепи.

Второй закон Кирхгофа.Второй закон Кирхгофа относится к контуру и записывается в виде

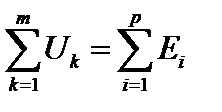. (2.5)

Приведенное выражение читается так: алгебраическая сумма падений напряжения на приемниках в любом контуре равна алгебраической сумме ЭДС, действующих в этом же контуре.

Поскольку в соответствии с законом Ома

I = U/R,

то выражение (2.5) можно записать в виде

,

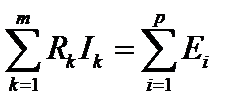т.е. в любом замкнутом контуре электрической цепи алгебраическая сумма падений напряжений на элементах, входящих в контур, равна алгебраической сумме ЭДС.

Правило знаков. Для составления уравнения по 2-му закону Кирхгофа выбирается произвольное направление обхода контура. Если направление тока в цепи совпадает с направлением обхода, то соответствующее слагаемое берется со знаком «+», а если не совпадает, то – со знаком «–». Аналогичное правило расстановки знаков справедливо и для ЭДС.

Пример 2.2. Записать второй закон Кирхгофа для контура, приведенного на рисунке.

Решение.

.

■

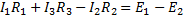Уравнение по 2-му закону Кирхгофа может быть записано и для контура, имеющего разрыв цепи, однако при этом необходимо в уравнении учитывать напряжение между точками разрыва.

Пример 2.3. Записать второй закон Кирхгофа для контура, выделенного на приведенной схеме (выделен пунктиром).

Решение.

■

Второй закон Кирхгофа по сути является законом баланса напряжений в контурах электрических цепей.