Анализ переходных процессов в электрических цепей постоянного тока методом переменных состояния.

Лекция 5-2014

Рассматриваемые вопросы:

2.8. Переходные процессы в линейных электрических цепях постоянного тока (методы переменных состояния и операторный)

Анализ переходных процессов в электрических цепей постоянного тока методом переменных состояния.

Из всех известных методов расчета переходных процессов наиболее физичным является метод пространства состояний. Этот метод позволяет одновременно получать все интересующие нас величины токов и напряжений.

Переменные состояния представляют собой систему наименьшего числа внутренних независимых величин необходимых для полного определения поведения динамической системы. Переменные состояния – это токи индуктивностей и напряжения емкостей, именно они определяют состояние системы. В математической форме уравнения состояний для сложной цепи имеют вид:

x (t) – вектор состояния (размерность n);

A – матрица состояния (размерность n×n );

BU(t) – вектор-столбец (размерность n);

D(x,t) – расширенная матрица.

Сначала рассмотрим составление уравнения состояния на простейших цепях первого порядка (рис. 2.57). Вектором состояния является напряжение на конденсаторе после коммутации. Запишем второй закон Кирхгофа.

Рис. 2.57

.

Перепишем это уравнение относительно производной .

или

.

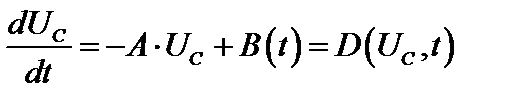Такой вид уравнения называется нормальным. Таким образом, дифференциальное уравнение, разрешенное относительно производной называется нормальным.

Рассмотрим еще один пример. Определим ток через индуктивность (рис. 2.58).

Рис. 2.58

В данном случае вектором состояния является ток через индуктивность. Составляем уравнение по второму закону Кирхгофа.

.

Разрешаем это уравнение относительно производной и получаем уравнение в нормальной форме

,

или

.

Рассмотрим пример для цепи второго порядка. Вектором состояния являются переменные

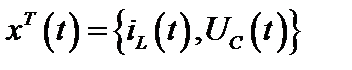
Записываем уравнения по второму закону Кирхгофа, в результате получаем систему дифференциальных уравнений:

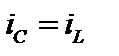
Разрешим эту систему относительно производных, то есть запишем в нормальном виде

Выпишем матрицу состояния:

,

, .

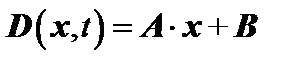Что бы проверить правильность составление матрицы состояния, нам нужно проверить ее собственные числа

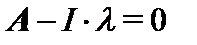
или

,

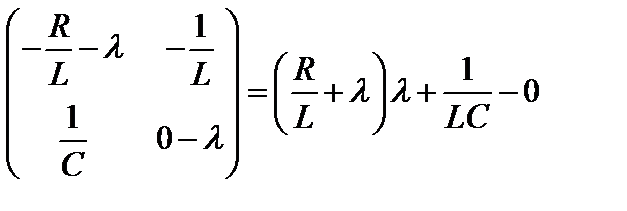откуда

.

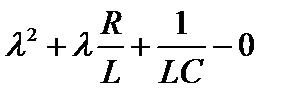Если все сделано правильно, то это уравнение совпадает с уравнением входного сопротивления схемы

.

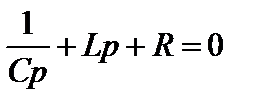Отсюда

или

.

Проверим столбцовую матрицу

.

Результат должен дать вынужденные составляющие напряжения на конденсаторе и ток через катушку индуктивности.

Пример 2.14. Для электрической цепи, изображенной на рисунке, определить ток i_L (t) в катушке индуктивности и напряжения u_C1(t) и u_C2(t) на конденсаторах после включе- ния ЭДС, если Е = 100 В, R₁ = 20 Ом, R₂ = 100 Ом, С₁ = 20 мкФ, L =0,01 Гн.

Решение. Запишем уравнения, связывающие токи i_C1, i_C2 и напряжение u_L1 с напряжениями на конденсаторах и током индуктивности. Для этого используются первый и второй законы Кирхгофа. В нашем примере матрицы x(t), A и BU (t) будут равны

, , .

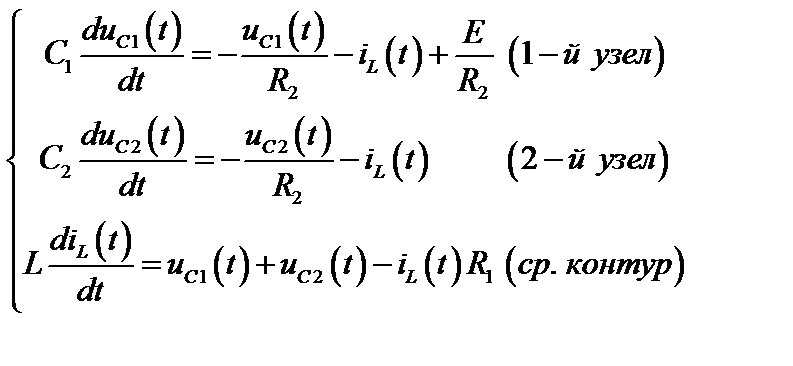
После подстановки числовых значений получаем:

, .

После определения матриц A и BF необходимо проверить правильность составления уравнения состояний. Это можно сделать, определив корни характеристического уравнения через входное сопротивление схемы:

Корни характеристического уравнения p₁, p₂, p₃ должны полностью совпасть с собственными числами λ₁, λ₂, λ₃ матрицы состояния А