Операторный метод анализа переходных процессов в электрических цепях постоянного тока.

Преобразование Лапласа и его свойства. Операторный метод берет начало со времени анализа бесконечно малых величин, когда были обнаружены определенные аналогии между дифференциально-интегральными и алгебраически-ми уравнениями. В XIX в. был опубликован ряд работ по операционному исчислению М.Е. Ващенко-Захарченко, О. Хэвисайда, Д. Карсона и др. Однако строгое обоснование операторный метод получил только в XX в. на базе общей теории функциональных преобразований.

В основе операторного метода расчета переходных процессов лежит преобразование Лапласа, которое позволяет перенести решение из области функций действительной переменной t в область комплексной переменной р:

При этом операции дифференцирования и интегрирования функций времени заменяются соответствующими операциями умножения и деления функций комплексной переменной на оператор р, что существенно упрощает расчет, так как сводит систему дифференциальных уравнений к системе алгебраических. В операторном методе отпадает необходимость определения постоянных интегрирования. Этими обстоятельствами объясняется широкое применение этого метода на практике.

Различают прямое и обратное преобразование Лапласа. Прямое преобразование Лапласа определяется уравнением

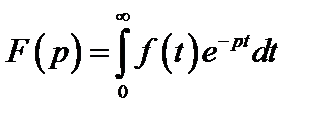, (2.18)

где - функция действительной переменной t, определенная при (при 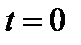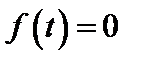) и удовлетворяющая условиям ограниченного роста

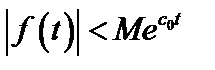
где множитель М и показатель роста с₀ - положительные действительные числа. На рис. 2.59 изображена область определения функции комплексной переменной F(p).

Рис. 2.59. Область определения функции комплексной переменной F(p)

Обратное преобразование Лапласа определяют из решения (2.18):

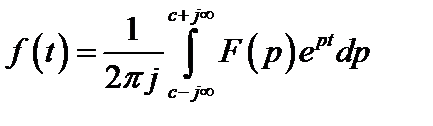(2.19)

Функция F(p), определяемая уравнением (2.18), носит название изображения по Лапласу, а функция f(t) в (2.19) — оригинала. Следовательно, оригинал и изображение пред­ставляют собой пару функций действительной f(t) и комплексной F(p) переменных, связанных преобразованием Лапласа. Для сокращенной записи преобразований (2.18), (2.19) используют следующую символику:

, , ,

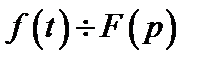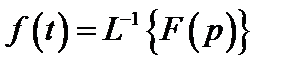
где L - оператор Лапласа. В дальнейшем для определенности будем использовать знак соответствия 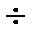или символ. .

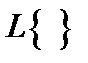Рассмотрим основные свойства преобразования Лапласа.

Свойство линейностиявляется следствием линейности преобразования Лапласа, его можно записать в форме

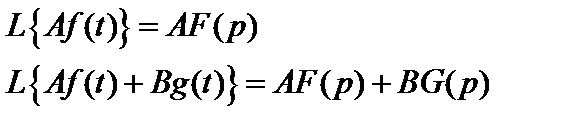(2.20.)

где А, В - постоянные коэффициенты разложения. Свойство (2.20) легко доказать, если применить к левой части соотношения (2.20) прямое преобразование Лапласа ( 2.18).

Дифференцирование оригинала.При ненулевых начальных условиях: f(0_) ≠ 0 дифференцирование ориги-нала соответствует следующему условию:

если

,

то

Применив эту теорему к производным высших порядков, получим

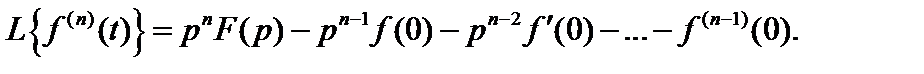(2.20, а)

При нулевых начальных условиях выражение (7.6) упрощается

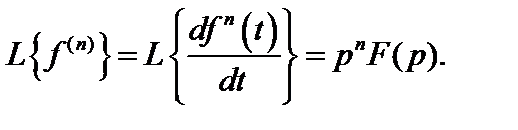
Интегрирование оригинала.Если

,

то

,

т.е. изображение интеграла кратности n функции f(t)

соответствует умножению изображения функции на при нулевых начальных условиях:

.

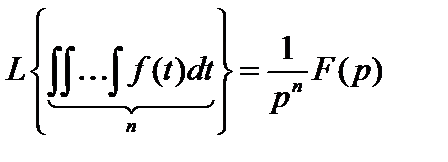Доказательство осуществляется путем использования свойства дифференцирования оригинала (7.6), (7.7).

Изменение масштаба независимой переменной(теорема подобия)

, (2.21)

где а - постоянный вещественный коэффициент. Свойство (2.21) легко доказывается путем замены независимой переменной τ = at в прямом преобразовании Лапласа (7.2).

Смещение в области действительной переменной(теорема запаздывания):

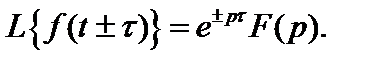(2.22)

Из соотношения (2.22) следует, что сдвиг оригинала по оси времени наτсоответствует умножению изображения на е^±pτ.

Смещение в области комплексной переменной(теорема смещения):

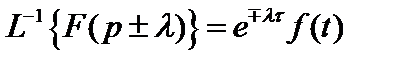(2.23)

Теорема (2.23) следует непосредственно из прямого преобразования Лапласа, если в (2.18) вместо f(t) подставить e^±λtf(t). Причем X может быть как действительной, так и комплексной величиной.

Дифференцирование и интегрирование оригинала по параметру(свойство коммутативности):

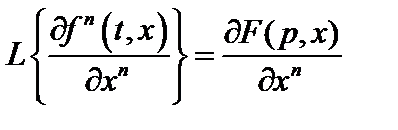, (2.24)

. (2.25)

Для доказательства свойств (2.24), (2.25) достаточно продифференцировать или проинтегрировать прямое преобразование Лапласа (2.18) по параметру х.

Произведение изображений:

(7.14)

Интегралы в (7.14) носят название свертки функци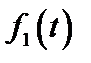й и .

Дифференцирование изображения:

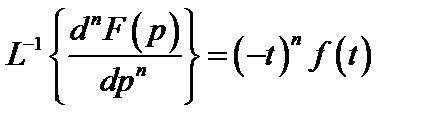.(7.15)

Интегрирование изображения:

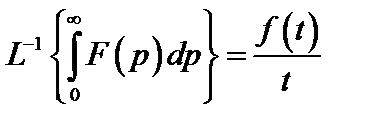(7.16)

Предельные соотношения для оригинала и изображения:

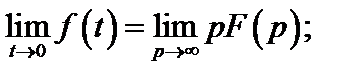
В качестве примера найдем изображение по Лапласу типовых сигналов. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используются различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательность прямоугольных импульсов и так далее. Особо важную роль в теоретических исследованиях электрических цепей играют испытательные сигналы в форме единичной функции 1(t) и единичной импульсной функции δ(t) (функция Дирака).

Единичная ступенчатая функция (функция Хэвисайда).Единичная функция (рис. 2.60, а) задается уравнением

Рис. 2.60.

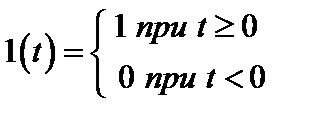. (2.26)

Изображение функции (2.26) будет равно:

, т.е. .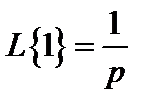

Единичная импульсная функция (функция Дирака). Она задается выражением

.

Функция Дирака является физически нереализуемой математической абстракцией, однако обладает рядом интересных свойств и играет очень важную роль в теоретических исследованиях. Формально она может быть получена, например, предельным переходом (при τ → 0) единичного импульса (см. рис. 2.61, б), площадь которого равна единице:

.

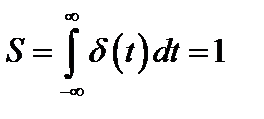Найдем изображение единичной импульсной функции в форме изображения разности двух единичных функций величины 1(t), сдвинутых друг относительно друга на τ (рис. 2.61).

Рис. 2.61.

Для этих функций с учетом теоремы запаздывания имеем:

,

.

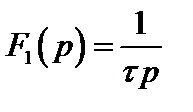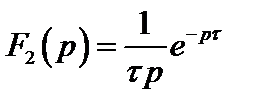Для результирующего изображения с учетом свойства линейностиполучим

.

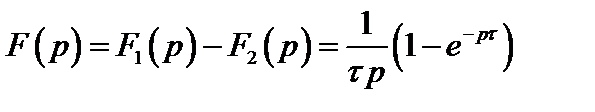При 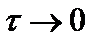изображение единичной импульсной функции

.

Экспоненциальный сигнал 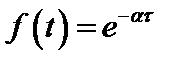при t > 0

,

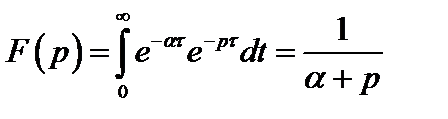т.е.

.

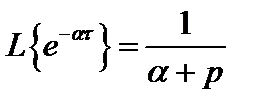Подобным же образом можно найти изображение по Лапласу других функций, удовлетворяющих условию (7.3). В литературе имеются специальные справочники, в которых приведены оригиналы и изображения широкого класса функций. В табл. 7.1 приведены оригиналы и их изображения наиболее часто встречающихся в теории электрических цепей функций.

Одним из интересных свойств функции δ(t) является ее фильтрующее свойство, определяемое равенством (рис. 2.62):

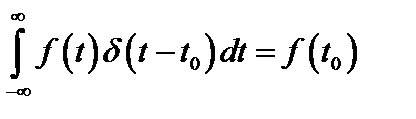
Рис. 2.62

Теорема разложения. Для нахождения оригинала по изображению можно воспользоваться либо таблицами, либо использовать обратное преобразование Лапласа (2.19). Однако вычисление оригинала с помощью (7.4) обычно оказывается весьма сложным. Поэтому, для упрощения расчетов применяют теорему разложения, которая позволяет при нахождении оригинала заменить операцию интегрирования в (2.19) операцией суммирования, что значительно упрощает вычисления. Наиболее строгий вывод этой теоремы можно осуществить на основании теоремы вычетов. Здесь мы ограничимся выводом формул разложения применительно к изображению, представляющему собой рациональную дробь:

, (*)

где a_n, a_n-1,…, a₁, a₀; b_m, b_m-1,…, b₁, b₀- вещественные коэффициенты, не имеющие общих корней.

Для нахождения оригинала 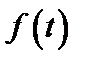разложим 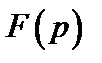на простые дроби

(2.27)

где 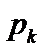− простые корни характеристического уравнения

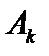− коэффициенты разложения.

Оригиналы и изображения некоторых функций приведены в следующей таблице.

Таблица 2.1

Оригиналы и изображения некоторых функций

№ п/п	Оригинал f(t)	Изображение F(p)
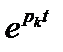
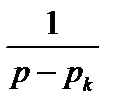
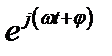
	1 -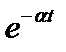
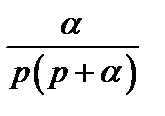
	sin ωt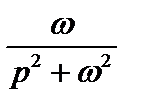
	sin (ωt + φ)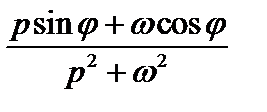
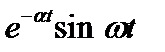
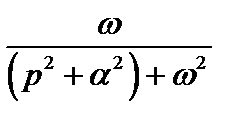
	cos ωt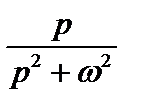
	cos (ωt + φ)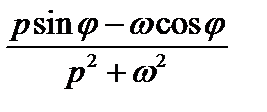
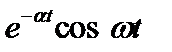
	A – const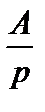
	At

,

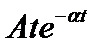
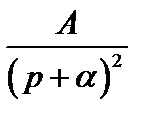
Для нахождения 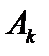умножим обе части последнего выражения на 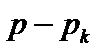и перейдем к пределу

.

По правилу Лопиталя в левой части с учетом того, что правая часть (2.27)) равна 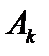, получаем

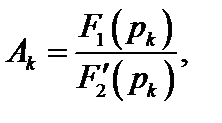
где

Подставим значение 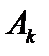в (2.27)

.

Поскольку изображение 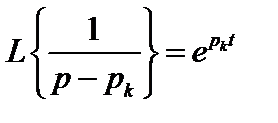(см. табл. 7.1), то

в соответствии со свойством линейности преобразования Лапласа окончательно получаем

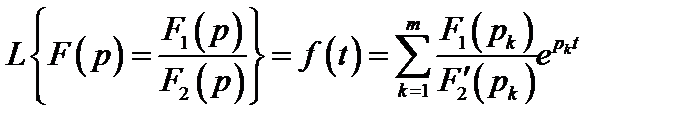. (2.28)

Последняя формула есть математическая формулировка теоремы разложения. Она позволяет найти оригинал по изображению в случае простых корней. Если же среди корней есть один нулевой 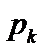, т.е. 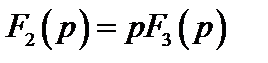, то теорема разложения примет вид:

. (2.29)

Формулу (2.29) можно получить, если подставить в (2.28) вместо F₂(p) значение pF₃(p) и осуществить операцию дифференцирования.

Если среди корней уравнения (2.27) (полюсов функции F(p)) имеются комплексно-сопряженные корни р_k и р_k+1, то в формуле (2.29) достаточно взять р_k, а для р_k+1 взять сопряженное значение, при этом сумма соответствующая двум этим корням с учетом дей­ствительности f(t) будет равна

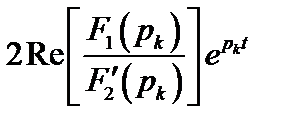
При этом в уравнении для f(t) появятся составляющие типа

Ae^-αtsin(ω_ct +θ).

Теорему разложения можно обобщить и на более общие случаи. В частности, если среди полюсов (*) имеются полюса кратности l, то в оригинале f(t) появятся слагаемые типа (6.8).

Пример 2.15. Получить оригинал функции , изображение которой имеет вид

.

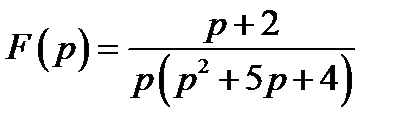Решение. Очевидно, что

,

.

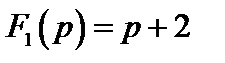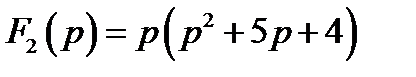Получим в виде (*).

Корни характеристического уравнения

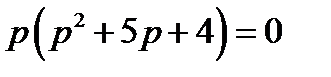
равны , , .

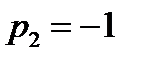Функция при p = p_k имеет значения , , .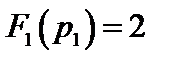

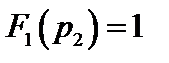Производная 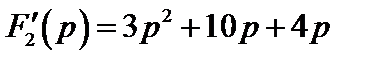при тех же значениях корней имеет значения 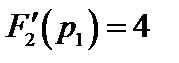, , 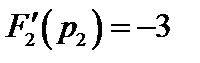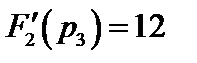. Теперь в соответствии с (7.30) окончательно получим

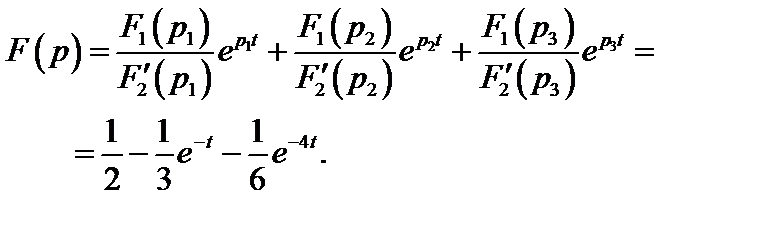
Учитывая, что среди корней характеристического уравнения F₂(p) = 0 имеем один нулевой корень, при нахождении f(t) можно было воспользоваться и формулой (7.31). Действительно, если обозначим

,

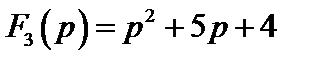то

.

Значения корней уравнения

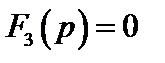
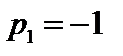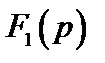будут равны , . Выражение функции принимает значения 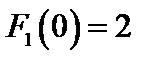, , , 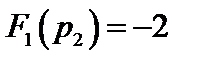а выражение производной

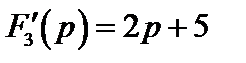
принимает значения , , .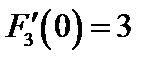

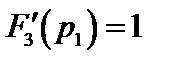С учетом полученных значений окончательно получим

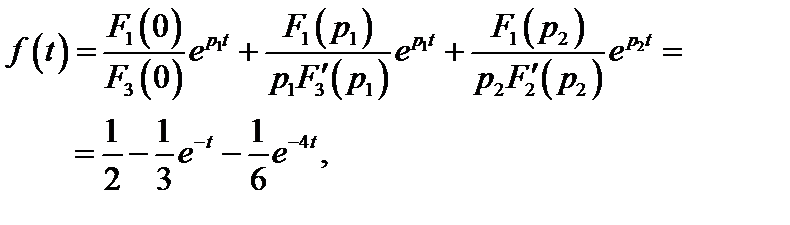
что полностью совпадает с предыдущим результатом.

Основные законы и элементы электрических цепей в операторной форме. Для получения операторных выражений законов электрических цепей необходимо получить операторные представления описаний этих законов в действительной форме.

Первый закон Кирхгофа: действительная формулировка – алгебраическая сумма токов ветвей сходящихся в узле в любой момент времени равна нулю

.

Преобразуем по Лапласу обе части этого равенства, учитывая свойство линейности (2.20). Тогда получим первый закон Кирхгофа в операторной форме

Его формулировка: алгебраическая сумма операторных токов ветвей, сходящихся в узле, равна нулю.

Второй закон Кирхгофа: действительная формулировка – алгебраическая сумма напряжений на ветвях замкнутого контура в любой момент времени равна нулю

На основании свойства линейности после преобразования по Лапласу этого равенства получим второй закон Кирхгофа в операторной форме

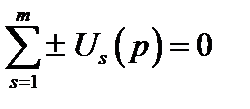
Его формулировка: алгебраическая сумма операторных напряжений на ветвях замкнутого контура равна нулю.

Закон Ома:Введем в рассмотрение операторное сопротивление Z(p) участка цепи, которое определим как отношение операторного напряжения к операторному току участка цепи при нулевых начальных условиях:

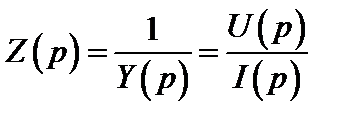
где 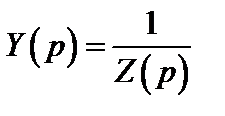− операторная проводимость.

Рассмотрим в качестве простейших участков цепи отдельные элементы: источник ЭДС, резистор, катушку индуктивности и конденсатор.

Источник ЭДС. Операторное представление источника получается простой заменой действительного обозначения операторным (рис. 2.63).

Рис. 2.63

Резистор. Мгновенные ток и напряжение связаны

законом Ома: 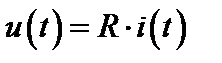(рис. 2.64, a).

a b

Рис. 2.64.

Преобразуем обе части этого равенства по Лапласу и получим закон Ома для резистора в операторной форме (рис. 4. b):

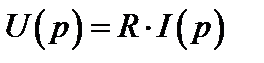
Операторные сопротивления и проводимость:

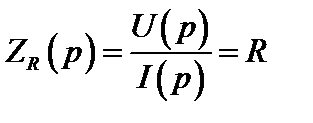
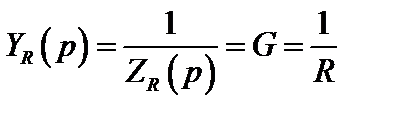
Катушка индуктивности. Напряжение u(t) и ток i(t) в катушке (рис. 2.65) связаны соотношением 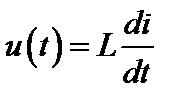(рис. 4. a). Будем предполагать нулевые начальные условия i_L(0)=0. Преобразуем обе части этого равенства по Лапласу.

Рис.2.65

Тогда согласно свойствам (3.1) и (3.2) получим:

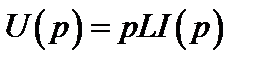
Полученное соотношение является алгебраическим (без операций дифференцирования или интегрирования) и его можно назвать законом Ома в операторной форме для индуктивности. При этом операторные сопротивление и проводимость индуктивности

, .

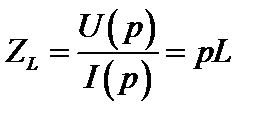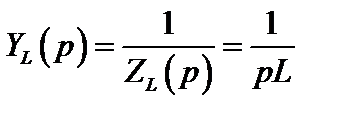Конденсатор. Связь между током и напряжением на емкостном элементе .

Рис. 2.66.

При нулевых начальных условиях (u_c(0) = 0) после преобразования этого равенства по Лапласу получим закон Ома в операторной форме для емкостного элемента:

, .

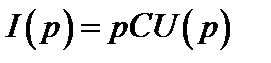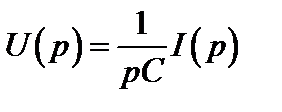Соответствующие операторные сопротивление и проводимость

, .

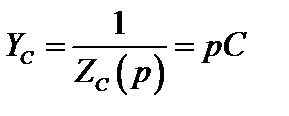Таким образом, закон Ома в операторной форме выполняется для всех трех элементов электрических цепей и может быть записан в обобщенном виде:

;

;

;

.

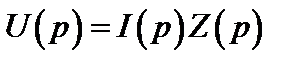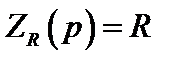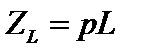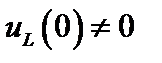Рассмотрим соотношения между операторными токами и напряжениями на элементах при ненулевых начальных условиях и . Очевидно, что изменения коснутся соответствующих уравнений для реактивных элементов, реальные токи и напряжения в которых связаны дифференциальными соотношениями.

Так для индуктивного элемента и после преобразования этого равенства по Лапласу согласно свойству (2.20, а) при ненулевых начальных условиях получим:

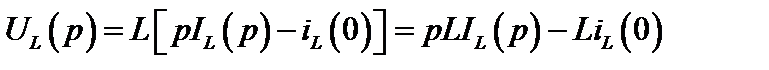(3.18)

Полученному уравнению соответствует так называемая операторная схема замещения индуктивности, которая представлена на рис. 2.67.

Рис. 2.67

Она содержит элемент с операторным сопротивлением 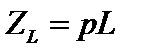, который моделирует падение напряжения от прохождения тока 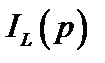(первое слагаемое в (3.18)), и источник напряжения (моделирующий второе слагаемое в (3.18)).

Аналогично для емкости 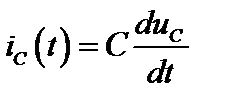после преобразования при ненулевых начальных условиях получим

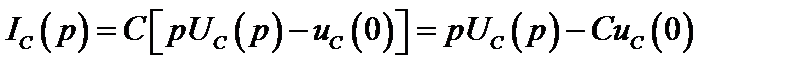
или

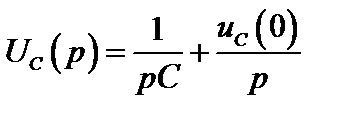(2.29)

В соответствии с (2.29) на рис. 2.68 представлена операторная схема замещения емкостного элемента.

Рис. 2.68.

Она содержит элемент с операторным сопротивлением и источник операторного напряжения 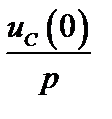, обусловленный ненулевым начальным условием.

Анализ переходных процессов операторным методом. Поскольку для операторных токов, напряжений и сопротивлений справедливы законы Ома и Кирхгофа, то расчет операторных токов и напряжений будет аналогичным расчету постоянных токов и напряжений в резистивных цепях постоянного тока. В частности, могут быть использованы все известные методы расчета (метод эквивалентных преобразований, метод узловых напряжений и т.д.), которые основаны на законах Ома и Кирхгофа. Учитывая изложенное, приведем методику решения задач операторным методом.

1. Определяются начальные условия 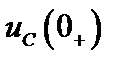и 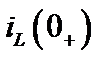обычным путем на основании законов коммутации.

2. Для цепи после коммутации составляется операторная схема замещения, в которой элементы представляются их операторными схемами замещения, реальные токи и напряжения заменяются операторными. Такой замене подвергаются как искомые токи и напряжения, так и известные токи и напряжения источников.

3. Для операторной схемы замещения определяются искомые операторные токи и напряжения с использованием законов Ома, Кирхгофа и всех методов расчета (эквивалентных преобразований, эквивалентного генератора, узловых напряжений и т.д.).

4. По найденным операторным токам и напряжениям определяются реальные токи и напряжения по таблицам или по формуле разложения, которая будет рассмотрена ниже.

Необходимо отметить, что при расчете переходных процессов операторным методом мы будем иметь дело с алгебраическими операциями над простейшими функциями переменной р каковыми являются операторные сопротивления и операторные функции источников (см. таблицу 3.1).

Пример 2.16. Для цепи на рисунке определить ток 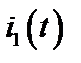после коммутации.

Начальные условия задачи нулевые 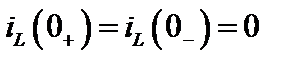. Поэтому в операторной схеме замещения не будет дополнительных источников. Операторная схема замещения показана на рис. 3.4. В ней представлены операторные сопротивления элементов и операторный искомый ток I₁(p) . Задающий ток I₀ источника постоянного тока преобразуется в задающий операторный ток согласно преобразованию Лапласа от постоянной величины (см. таблицу 3.1 соответствие 2).

Для определения тока 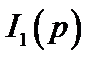в операторной схеме замещения можно использовать метод эквивалентных преобразований: определить эквивалентное сопротивление относительно зажимов источника, затем напряжение 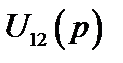на зажимах источника (оно же действует и на резисторе R₁) и наконец, ток .

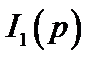Операторное сопротивление последовательной цепи R₂L - 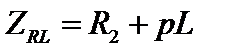; эквивалентное операторное сопротивление соответствует параллельному соединению ветвей R₁ и Z_RL(p) и равно

.

Операторное напряжение на резисторе R₁

Искомый операторный ток:

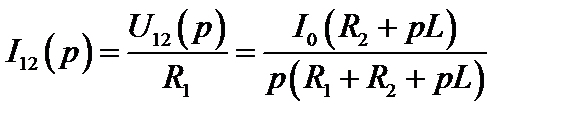
Приводим его к табличному виду:

К оригиналу переходим по таблице 2.1, от каждого слагаемого по отдельности, используя соответствия 4 и 3:

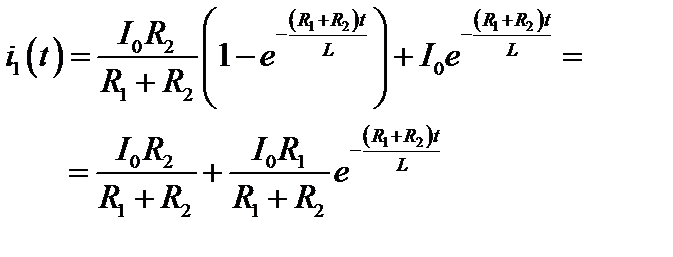
График i₁(t) приведен на рис. 3.5.

■

Операторная функция передачи и ее основные свойства. Операторной функцией передачи называется отношение операторной реакции цепи к операторному воздействию при нулевых начальных условиях.

Если воздействие и реакция являются напряжениями (рис. 3.8), то операторная функция передачи

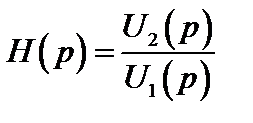(2.30)

Другие возможные варианты:

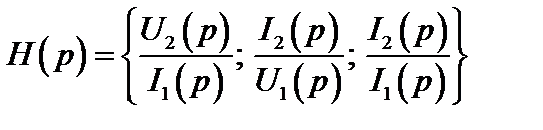
В определении индекс 1 относится к воздействию, а индекс 2 – к реакции. В дальнейшем будем рассматривать (2.30) имея в виду, что полученные результаты будут справедливы и для других вариантов функции передачи. Из определения следует, что передаточная функция связывает реакцию и воздействие:

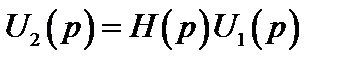(2.31)

Рис. 2.67.

Таким образом, по известной операторной функции может быть определена реакция цепи на заданное воздействие. Причем это может быть сделано в самом общем переходном режиме работы электрической цепи. Поэтому операторная функция передачи содержит полную информацию о цепи, является самой общей функцией цепи и по ней, как будет показано, могут быть определены все другие функции цепи (АЧХ, ФЧХ, переходная, импульсная).

Если рассматривать электрическую цепь с двумя зажимами (двухполюсник), тогда и воздействие и реакция (U₁(p); I₁(p)) будут определяться на одной паре зажимов. При этом в качестве операторной функции передачи, как частный случай, рассматривается входная функция: операторное сопротивление или операторная проводимость .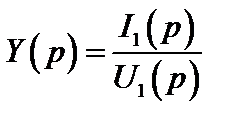

В качестве примера рассмотрим определение операторной функции передачи для последовательного RCL – контура, когда реакцией является напряжение на емкости, а воздействием – напряжение на входе цепи (рис. 2.69)

Рис. 2.69.

Общий подход к определению функции передачи следующий: считаем, что операторное воздействие U₁(p) задано и любым известным методом определяем выражение для операторной реакции. При этом получим выражение вида (2.31), из которого легко определить функцию передачи.

Руководствуясь этим подходом, определим:

;

;

,

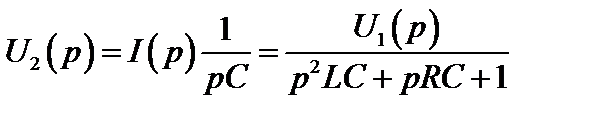где p₁ и p₂ корни полинома знаменателя функции передачи.

В данном случае получили функцию передачи с полиномом второго порядка относительно комплексной переменной (оператора) p в знаменателе. Коэффициенты этого полинома определяются вещественными параметрами цепи.

В общем случае операторная функция передачи является дробно-рациональной (отношение полиномов) функцией с вещественными коэффициентами:

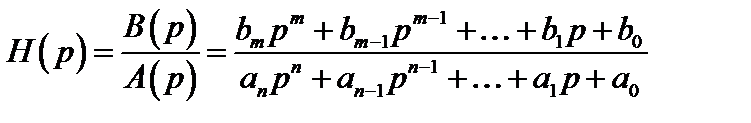(2.32)

Это утверждение следует из того, что H(p) получается в результате рациональных алгебраических операций с элементами операторной схемы замещения 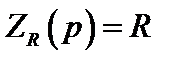; ; 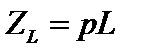, которые представляют собой простейшие дробно-рациональные выражения относитель-но комплексной переменной p.

Степени полиномов числителя и знаменателя функции передачи зависят от числа реактивных элементов и схемы цепи. Если в (2.32) полиномы числителя и знаменателя представить в виде произведения множителей - двучленов, то получим так называемое полюсно-нулевое представление функции передачи

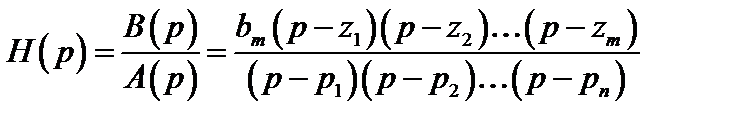(3.27)

где z_i (i=1,2…m) − корни полинома числителя, которые называются нулями функции передачи; p_k (k = 1,2…n) − корни полинома знаменателя, которые называются полюсами функции передачи. Нуль представляет значение комплексной переменной, при котором функция передачи обращается в нуль, а полюс – значение комплексной переменной, при котором функция передачи обращается в бесконечность. Нули и полюсы функций цепи, имеющих вещественные коэффициенты, могут быть вещественными, (p_k = a_k) либо комплексными попарно сопряженными

Рассмотрим взаимосвязь операторной функции передачи и дифференциального уравнения цепи. Для этого перепишем (2.31), используя (2.32), в следующем виде

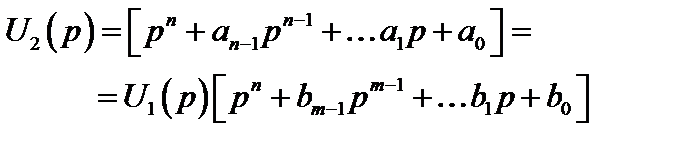
Согласно свойству об изображении производной преобразования Лапласа при нулевых начальных условиях умножение изображения на p^k соответствует взятию k-той производной от оригинала. Учитывая это и переходя к оригиналам от обеих частей равенства, получим дифференциальное уравнение

(2.33)

Таким образом, функция передачи, найденная из операторной схемы замещения, фактически представляет собой символическую запись дифференциального уравнения относительно выбранной переменной. Очевидно, что характеристическое уравнение для дифференциального уравнения (2.33) имеет вид

(2.34)

Таким образом, характеристический полином (2.34) совпадает с полиномом знаменателя функции передачи (2.32). Корни характеристического уравнения совпадают с полюсами операторной функции передачи p_k и определяют свободную (собственную) составляющую реакции:

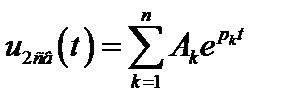(2.35)

где A_k – постоянная интегрирования.

Операторные функции передачи устойчивых цепей.Электрическая цепь считается устойчивой, если свободные колебания ограничены u_2св(t) ® 0 при t®¥. Свободные колебания определяют переходный процесс и согласно (2.35) зависят от полюсов операторной функции передачи. Для реальных RLC – электрических цепей, полюсы функции передачи можно подразделить на два вида:

1. Вещественные p_k = a_k.

2. Комплексные попарно сопряженные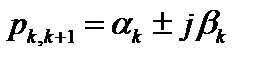

В первом случае соответствующее слагаемое в (3.30)

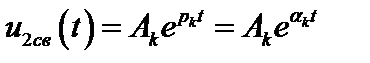
и для устойчивой цепи должно выполняться условие: a_k < 0, т. к. в противном случае рассматриваемое слагаемое дает неограниченное возрастание колебаний (рис. 2.70)

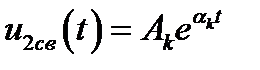
Рис. 2.70.

Во втором случае

,

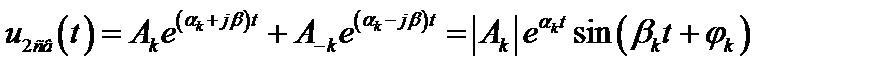где A_k и A_-k комплексные сопряженные числа.

Рассматриваемое слагаемое представляет собой синусоидальное колебание, амплитуда которого изменяется по экспоненциальному закону с показателем a_k. Если этот показатель будет отрицательным, то колебания будут затухающими (рис. 2.71, а), в противном случае – возрастающим (рис. 2.71, б).

Рис. 2.71.

Таким образом, для устойчивых цепей операторная функция передачи должна иметь полюсы с отрицательными вещественными частями. Для наглядности полюсы изображают на плоскости комплексного переменного p в виде крестиков. На рис. 2.72 изображены полюсы некоторой устойчивой цепи с отрицательными вещественными частями.

Рис. 2.72.

Как видно полюсы функций передачи устойчивых цепей располагаются в левой полуплоскости комплексной переменной p.